Казанский государственный энергетический университет Кафедра «Высшей математики»

Опорные конспекты лекций.

Тема : Определенный интеграл.

Метод интегральной суммы.

Опр. Аддитивной величиной наз. параметр физической системы Р, который можно представить как сумму его значений от всех составных частей системы P = p_i .

Например, площадь фигуры, объем тела, длина пройденного пути. Разбиение на составные части в этих случаях совершенно произвольно. Разделение пространственного объекта можно довести до уровня отдельной точки, затем определить в ней значение нужного параметра, но вот вычислить сумму бесконечно большого числа таких слагаемых прямым суммированием нельзя. Приходится вводить специальную процедуру суммирования “точечных” параметров - метод интегральной суммы.

З адача. Вычислить площадь круга радиуса R.

Строим вписанный в круг n – угольник и соединяем его вершины с центром. Тогда АОС = 2 = 2 /n , AC = =2AB = 2R sin , S_AOC = AB BO = Rsin Rcos = ½ R²sin2 . Площадь многоугольника S_n = n S_AOC в пределе n переходит в площадь круга S = lim S_n =

=½ R² lim n sin 2 /n = R² lim sin(2 /n)/(2 /n) = R²

Последовательность действий: имеем основную фигуру, разделяем ее на n участков, вычисляем площадь одного треугольника, вычисляем общую площадь треугольников, переходим к пределу. Эта процедура носит универсальный характер.

Алгоритм метода интегральной суммы.

1. Исследуемая аддитивная система разделяется на n однотипных участков (разбиение Z).

2. Для каждого участка устанавливается некоторое приближенное значение аддитивного параметра p_{i .}

3. Проводится суммирование приближенных значений аддитивного параметра по всем n участкам P(n) = p_i

4. Переход к пределу lim P(n) = P при n дает точное решение задачи, т.е. определяет значение искомого параметра для всей системы

Опр. Интегральной суммой наз. сумма всех приближенных значений аддитивного параметра, определенных для каждого из n участков на которые была разделена исследуемая система .

Опр. Предел интегральной суммы, полученной путем разбиения пространственного объекта на составные части, наз. интегралом (определенным).Это главный параметр суммы

В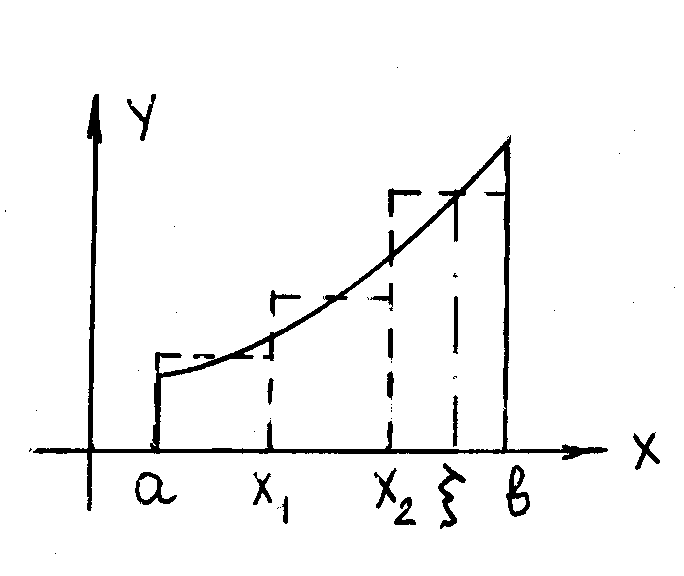 ид суммы и её предела определяется условиями задачи и числом использованных переменных. Существуют двойные, тройные, криволинейные, поверхностные интегралы.

Площадь криволинейной трапеции

Опр. Фигура ограниченная графиком функции y = f(x) на промежутке [a,b], осью Ох и двумя перпендикулярами, восстановленными из точек a и b наз.криволинейной трапецией.

Метод интегральной суммы:

1) Отрезок [a, b] разделим на n равных частей точками x_i = a + i x, где i = 0,1,2, …,n и x = (b – a)/n . Из точек x_i восстановим перпендикуляры и соединим их прямыми | | оси Ох на высоте f( _i), где x_{i i} x_i+1 . Получим вспомогательную, ступенчатую фигуру, составленную из прямоугольников. 2) Площадь одного прямоугольника f( _i) x_i . 3) Площадь всей вспомогательной фигуры, т.е. интегральная сумма, равна

S_n = f( _i) x_i ( 1 )

Чем больше n, тем точнее приближение, а предел n должен дать точный результат

Опр. Определенным интегралом от функции f(x) на промежутке [a,b] наз. предел интегральной суммы, полученный путем разбиения промежутка на малые участки.

lim f( _i) x_i = f(x) dx ( 2 )

Здесь а – нижний предел, b – верхний предел, а сам символ повторяет основные элементы интегральной суммы. Введен Лейбницем.

Геометрический смысл определенного интеграла – площадь криволинейной трапе-ции. Геометрический смысл интегральной суммы – площадь вспомогательной фигуры.

Основные свойства определенного интеграла.

1⁰ A f(x)dx = A f(x)dx

Постоянный множитель выносится за знак интеграла, т.к. он может быть вынесен за знак суммы.

2⁰ [f(x) + g(x)] dx = f(x) dx + g(x) dx

Интеграл от суммы функций равен сумме интегралов, т.к. предел от суммы функций равен сумме пределов.

3⁰ f(x) dx = f(x) dx = f(x) dx (a < c < b)