5. Энергия упругой деформации
Любое упруго деформированное тело обладает потенциальной энергией, так как изменяется взаимное расположение отдельных частей тела. Рассмотрим случай растяжения пружины.
Растяжение
будем производить очень медленно, чтобы
силу
,
с которой мы действуем на пружину, можно
было считать все время равной по модулю
упругой силе
.
Тогда
где к, х –
соответственно жесткость и удлинение
пружины. Тогда работа, которую нужно
совершить, чтобы вызвать удлинение (или
сокращение) х
пружины,
равна
(5.16)
Эта работа идет на увеличение потенциальной энергии пружины. Следовательно, зависимость потенциальной энергии пружины от удлинения х имеет вид
, (5.17)
если считать, что потенциальная энергия недеформированной пружины равна нулю.
Потенциальная энергия упруго деформированного стержня равна
,
(5.18)
где
–
объем стержня.
Отношение
энергии
к тому объему
,
в котором она заключена, называется
плотностью
энергии u.
Тогда
– плотность энергии упругой деформации
при растяжении (или сжатии).
6. Закон сохранения и превращения механической энергии
Рассмотрим
систему, состоящую из двух материальных
точек с массами
.
Пусть частицы взаимодействуют друг с
другом с силами
,
модули которых зависят только от
расстояния между материальными точками
.
Такие силы являются консервативными.
Предположим, что, кроме консервативных
сил, на каждую точку действуют внешняя
консервативная сила
и внешняя неконсервативная сила
.
Тогда уравнение движения каждой точки
имеет вид:
,
(5.19)
Умножив
уравнения (5.19) на соответствующие
перемещения
,
учитывая определение ускорения
материальной точки и сложив вместе
полученные уравнения, имеем
(5.20)
Левая часть представляет собой приращение кинетической энергии системы:
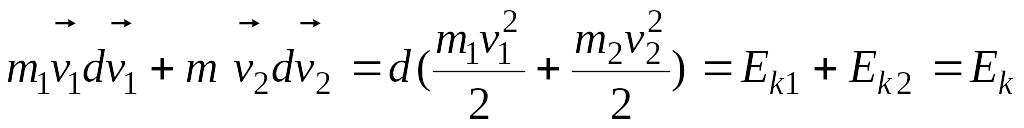(5.21)
Первый
и четвертый члены правой части равны
убыли потенциального взаимодействия
частиц:
(5.22)
Второй
и пятый члены правой части равны убыли
потенциальной энергии во внешнем поле
консервативных сил:
.
Остальные члены представляют собой работу неконсервативных внешних сил:
(5.23)
Приняв во внимание (5.21)-(5.23), представим соотношение (5.20) следующим образом:
(5.24)
Величина
есть полная механическая энергия
системы. Если внешние неконсервативные
силы отсутствуют, правая часть формулы
(5.23) будет равна нулю и, следовательно,
полная энергия системы остается
постоянной:
(5.25)
Таким образом, мы пришли к выводу, что полная механическая энергия системы тел, на которые действуют только консервативные силы, остается постоянной. В этом и заключается закон сохранения механической энергии.
Для замкнутой системы, т.е. системы, на тела которой не действуют никакие внешние силы, соотношение (5.25) имеет вид
(5.26)
В этом случае закон сохранения механической энергии формулируется следующим образом: полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остается постоянной.
Если в замкнутой системе кроме консервативных действуют также неконсервативные силы, например силы трения, то полная механическая энергия системы не сохраняется. Рассматривая неконсервативные силы как внешние, можно в соответствии с (5.24) написать
(5.27)
Пример. Основными запасниками механической энергии во время бега и других циклических движений являются сухожилия. Каждый из нас может убедиться, что механическая энергия действительно запасается в наших ногах, как в пружинах. Сильно сгибая ноги в этом можно убедиться. Мы сразу заметим, что подниматься гораздо легче, если выпрямить ноги сразу, чем если задерживаться на секунду. Это можно объяснить тем, что при сгибании колен часть мышц напряжена, контролируя движение вниз, и их сухожилия растянуты. Если перед подъемом сухожилиям не дать возможность укоротиться, запасенная в них потенциальная энергия перейдет в кинетическую. В этом случае выполняется закон сохранения механической энергии для замкнутой системы тел. В противном случае между мышцами появляются неконсервативные силы, что проявляется в нагреве тела: полная механическая энергия системы не сохраняется, часть механической энергии переходит в тепловую.
Свойства сухожилий более или менее одинаковы у всех животных. Однако конечности копытных, например, овец и лошадей, наиболее приспособлены для хранения механической энергии. Некоторые мышцы в нижних частях ног этих животных состоят практически целиком из одних сухожилий. Самым выразительным примером такого использования сухожилий могут служить нижние конечности верблюда. В ноге человека самым мощным является ахиллово сухожилие, на которое при беге может действовать растягивающая сила до 4000 Н.