- •Б. 11. 1.Уравнения max работы Гиббса-Гельмгольца, их вывод и анализ.
- •Б.11.2.Активности компонентов раствора. 3 шкалы активности.
- •Б.12.1.Статистический хар-р 2 закона термодинамики. Ур. Больцмана, его вывод и анализ.
- •Б.12.2.Осмос. Вывод уравнения для расчета осмотического давления.
- •Б. 13.1.Термодин. Потенциалы идеальных и реал. Газов. Летучесть реал. Газа и ее расчет.
- •Б.13.2. Гетерог. Равновесия. Составл. В-ва системы, комп-ты, фазы, степ. Свободы. Правило фаз.
- •Б.14.1.Фаз. Переходы I рода для индив. В-в. Урав. Клапейрона-Клаузиуса. Фаз. Переходы II рода.
- •Б.14.2. Диаграммы состояния воды, серы, бензофенона.
- •Диаграмма состояния серы
- •Б. 15.1. Уравн. Для характер. Функций многокомпон. Систем, . Урав. Гиббса-Дюгема.
- •Б.15.2. Условия хим. Равновесия. Здм (вывод, анализ). Разл. Формы выражения к равн.
- •Б.16.1.Давление нас. Пара бинарных р-ров. Закон Рауля. Ид. Растворы. Предельно разбавл. Р-ры.
- •Б.16.2. Влияние т на хим. Равновесие. Уравн. Изохоры и изобары –ц-, их вывод, анализ, интегр-е.
- •Б. 17.1.Отклонения от законов идеальных растворов, причины отклонений.
- •Диаграмма сост. Системы, образ. Хим. Соединение, плавящееся инконгруентно (с разложением).
- •Б.18.1.Огр. Взаим. Р-ть жидкостей. Р-ть газов в жидкостях. З. Генри, Дальтона, Сеченова. Влияние t0.
- •Б.18.2.Трехкомпонентные системы. Способы изобр. Состава. Диаграмма с тройной эвтектикой.
- •Б.19.1.Растворимость тв. В-в в жидкостях. Уравнен. Р-ти в ид. И пред. Разб. Р-рах. Откл. От ид. Р-ти.
- •Б.19.2. Диаграмма состояния 2хкомпонентной системы с неогр. Взаимной р-тью компонентов.
Б.14.1.Фаз. Переходы I рода для индив. В-в. Урав. Клапейрона-Клаузиуса. Фаз. Переходы II рода.
Фаз.
переходы
(т.е. превращения агрегатных состояний)
возможны в системе, сост. из неск. фаз
чистого в-ва, находящихся в равновесии.Рассм.
равновесный переход 1 моля в-ва из фазы
1 в фазу 2 при Р,Т = const
(жидкость – газ).U2
– U1
= Q
– A
= T
(S2
– S1)
– P
(V2
– V1)
(только А расширения) U2
– TS2
+ PV2
= U1
– TS1
+ PV1;
G2
= G1.
Изобар.
пот-лы единицы m
чистого в-ва в 2х фазах, нах-ся в равновесии,
равны м/у собой.
Для
полных дифф-лов: dG1
= V1dP
– S1dT
,
dG2
= V2dP
– S2dT;
dG2
– dG1
= (V2
– V1)dP
– (S2
– S1)dT
= 0 (= 0, т.к. сохран. фазовое равновесие
и dG1
= dG2).
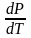 =
=
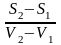 Т.к.
–ц- равновесн. и изотерм., то можно
записать: S2
– S1
= Q/T
= Н/T
; Q – Q,поглощ.
при переходе 1 моля в-ва из одной фазы в
др; Н
– теплота фазового превращения;
Т
– Т фазового превращения;
V2
– V1
–
р-ть мольных объемов 2х фаз.
=
Т.к.
–ц- равновесн. и изотерм., то можно
записать: S2
– S1
= Q/T
= Н/T
; Q – Q,поглощ.
при переходе 1 моля в-ва из одной фазы в
др; Н
– теплота фазового превращения;
Т
– Т фазового превращения;
V2
– V1
–
р-ть мольных объемов 2х фаз.
=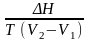 ,
Н
= Т
(V2
– V1)
-
урав. Клапейрона-Клаузиуса
–общее термодинам. уравн, подходит ко
всем превращениям агрегатных состояний
чистых в-в. ФАЗ.
ПЕРЕХОДЫ I
РОДА
– фаз.
переходы, характериз-ся равенством
изобарн. потенциалов 2х сосуществующих
в равновесии фаз и скачкообразным
изменением S
и V
при переходе в-ва из одной фазы в др.
(плавление,
испарение, возгонка, переход из одной
кристалл. модификации в др.).
,
Н
= Т
(V2
– V1)
-
урав. Клапейрона-Клаузиуса
–общее термодинам. уравн, подходит ко
всем превращениям агрегатных состояний
чистых в-в. ФАЗ.
ПЕРЕХОДЫ I
РОДА
– фаз.
переходы, характериз-ся равенством
изобарн. потенциалов 2х сосуществующих
в равновесии фаз и скачкообразным
изменением S
и V
при переходе в-ва из одной фазы в др.
(плавление,
испарение, возгонка, переход из одной
кристалл. модификации в др.).
ПЛАВЛЕНИЕ.
=
 ;
Нпл
всегда
0; Vж
Vтв
для большинства в-в, т.е. плотность тв.
фазы > плотн. жидкой. След-но,
;
Нпл
всегда
0; Vж
Vтв
для большинства в-в, т.е. плотность тв.
фазы > плотн. жидкой. След-но,
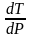 =
=
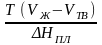
0 и с ростом Р температура плавл.
повыш-ся.
0 и с ростом Р температура плавл.
повыш-ся.
ИСПАРЕНИЕ
(ВОЗГОНКА).
=
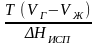
0 ; (Нисп
всегда
0; Vг
Vж
для всех в-в, и поэтому Ткип
всегда ↑ с ростом Т). Если Т далека от
крит., Vг
Vж,
то Vж
можно пренебречь.
0 ; (Нисп
всегда
0; Vг
Vж
для всех в-в, и поэтому Ткип
всегда ↑ с ростом Т). Если Т далека от
крит., Vг
Vж,
то Vж
можно пренебречь.
Нисп
= Т
Vг.
Если нас. пар можно считать ид. газом,
то Нисп
= Т
,
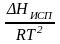 =
=
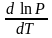
Давление нас. пара жидкости можно измерить в шир. интервале Т; значит. труднее измерить Нисп. Интервал Т д.б. небольшим, т.к. Нисп изменяется с ростом Т. Более точно Нисп вычисляют
|
по значению dP/dT, j находят, определив наклон касательной к кривой Р = f (Т) при заданной Т. Зав-ть Нисп от Т: убывает с ростом Т, не сильно изменяясь при средних Т и очень сильно – вблизи Ткр, при которой Нисп становится =0. Нисп различных жидкостей связаны с их НТК: 1.
Правило
Трутона:
Sисп
=
мольные энтропии испарения разл. жидкостей в НТК одинаковы. |
2. Урав. Кистяковского (более точное): Sисп = = 8,75 + 4,57 ln Ткип ( ) 3. Прав. Гильдебранда – Sисп жидкостей равны м/у собой при Т, для j мольные объемы нас. пара одинаковы, при этом Sисп = 20 – 22 при Vг = 49,5 л/моль. Эти правила не выполн. для ассоциированных жидк. (вода,спирты), и приблиз. выпол. для углеводородов и их произв.,эфиров и др. неполярных в-в.
Для ФАЗ. ПЕРЕХОДОВ II РОДА. хар-но не только рав-во изобар. пот-лов, но и рав-во S и V сосуществующих в равновесии фаз, т.е. отсут. тепл. эффекта –ц- и изменения V при Т превращения:
G = S = V = 0; Но меняются скачкообразно др. параметры, н-р, СР. Примеры ФП II рода:
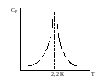
1. Скачкообр. изменение СР при превращении 2х модификаций жидкого He при 2,2 К.
|
В некот. интервале Т в-во поглощает значительно большее кол-во Q, чем то, которое соответствовало бы кривой при отсутствии пика. Эта доп. теплота связана с превращением 2-го рода, но она поглощается в некотором интервале Т и вызывает аномальное увеличение СР в этом интервале; при Т максимума кривой теплота не поглощается. 2. Превращения ферромагнитных тел при Т, назыв. точкой Кюри, выше j тела теряют ферромагнитные. св-ва. 3.Превращения обычных металлов в |
сверхпроводники при низких Т. 4.-Ц- распада и образования интерметаллидов в тв. метал. р-рах.

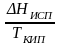
20 – 22
20 – 22
 –
–