
- •Б. 11. 1.Уравнения max работы Гиббса-Гельмгольца, их вывод и анализ.
- •Б.11.2.Активности компонентов раствора. 3 шкалы активности.
- •Б.12.1.Статистический хар-р 2 закона термодинамики. Ур. Больцмана, его вывод и анализ.
- •Б.12.2.Осмос. Вывод уравнения для расчета осмотического давления.
- •Б. 13.1.Термодин. Потенциалы идеальных и реал. Газов. Летучесть реал. Газа и ее расчет.
- •Б.13.2. Гетерог. Равновесия. Составл. В-ва системы, комп-ты, фазы, степ. Свободы. Правило фаз.
- •Б.14.1.Фаз. Переходы I рода для индив. В-в. Урав. Клапейрона-Клаузиуса. Фаз. Переходы II рода.
- •Б.14.2. Диаграммы состояния воды, серы, бензофенона.
- •Диаграмма состояния серы
- •Б. 15.1. Уравн. Для характер. Функций многокомпон. Систем, . Урав. Гиббса-Дюгема.
- •Б.15.2. Условия хим. Равновесия. Здм (вывод, анализ). Разл. Формы выражения к равн.
- •Б.16.1.Давление нас. Пара бинарных р-ров. Закон Рауля. Ид. Растворы. Предельно разбавл. Р-ры.
- •Б.16.2. Влияние т на хим. Равновесие. Уравн. Изохоры и изобары –ц-, их вывод, анализ, интегр-е.
- •Б. 17.1.Отклонения от законов идеальных растворов, причины отклонений.
- •Диаграмма сост. Системы, образ. Хим. Соединение, плавящееся инконгруентно (с разложением).
- •Б.18.1.Огр. Взаим. Р-ть жидкостей. Р-ть газов в жидкостях. З. Генри, Дальтона, Сеченова. Влияние t0.
- •Б.18.2.Трехкомпонентные системы. Способы изобр. Состава. Диаграмма с тройной эвтектикой.
- •Б.19.1.Растворимость тв. В-в в жидкостях. Уравнен. Р-ти в ид. И пред. Разб. Р-рах. Откл. От ид. Р-ти.
- •Б.19.2. Диаграмма состояния 2хкомпонентной системы с неогр. Взаимной р-тью компонентов.
Б. 13.1.Термодин. Потенциалы идеальных и реал. Газов. Летучесть реал. Газа и ее расчет.
1.
U
1 моля ид. газа,
зависящая только от Т: dU
= CV
dT
, U
= Uo
+
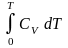
2.
H:
H = U + PV = Uo
+
+ RT = Uo
+
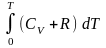 = Uo
+
= Uo
+
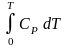
3.S: S = CV ln T + R ln V + So , S = CP ln T R ln P + So
4. dF = – PdV – SdT , dG = VdP – SdT
Пусть
T=const: dF = –PdV = –
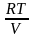 dV,
dG = VdP =
dV,
dG = VdP =
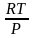 dP;
F = –RT ln
V + F(T) , G = RT ln
P + G(T)
dP;
F = –RT ln
V + F(T) , G = RT ln
P + G(T)
|
Для
реал. газов Льюис предложил
формальный прием, j
позвол. связать найденные опыт. путем
св-ва реал. газа с его термодин. пар-рами
и изучать т.о. термодинам.закономерности
в реал. газ. системах. Вводится
новая функция f
– термодинам. летучесть (летучесть,
фугитивность.
f
подставл. в урав. вместо Р. G=RTlnf+G(T)
(1).
При этом вводится условие:
|
=
RT
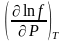 ;
Т.к.
= V,
то V
= RT
;
Т.к.
= V,
то V
= RT
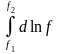 =
=
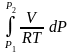 , ln
, ln
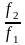 =
=
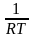
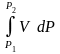
Надо знать зав-ть V от Р. Наиб. точный способ закл. в граф. нахождении интеграла. По эксперим. значениям V строят кривую зависимости V от Р. Интеграл = площади под кривой. Зная V = V(P), вычисл. объемную поправку реального газа : V = – , 0 при не слишком высоких Р
ln
=
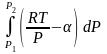 = ln
= ln
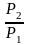 –
–
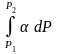 , надо знать
=
(Р). ln
f2
– ln
f1
= ln
P2
– ln
P1
–
, надо знать
=
(Р). ln
f2
– ln
f1
= ln
P2
– ln
P1
–
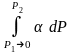
Пусть нижний предел интегрирования Р1 очень мал, так чтобы f1 = P1 :
ln
f
= ln
P –
; ln
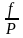 = –
,
= exp
(–
)
= –
,
= exp
(–
)
= - коэф. активности или коэф. летучести газа. Изобразим зав-ть = – V от Р, характерную для многих реал. газов при обычной Т:
|
1. При высоких Т мало изм. с ростом Р в широком интервале Р 2. Площадь под кривой от Р = 0 соответствует величине интеграла 3. При повышении Р для многих газов меняет знак. Поэтому летучесть многих реал. газов сначала < Р, потом = Р, а затем > Р (при бол. Р).Если Т – высокие, Р – невысокие, = const, тогда: ln
f
= ln
P
–
При мал. и Р функция м.б. разложена в ряд Маклорена (2 члена) |
=
1 –
=
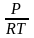 (
– )
=
(
– )
=
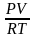 =
=
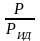 ;
(
– объем ид. газа; V
– объем реал. газа). Здесь Рид
– давл., j
имел бы ид. газ, если бы он занимал тот
же V,
j
занимает реал. газ.
=
, f
=
;
(
– объем ид. газа; V
– объем реал. газа). Здесь Рид
– давл., j
имел бы ид. газ, если бы он занимал тот
же V,
j
занимает реал. газ.
=
, f
=
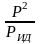 . Это дает возм-ть приближенно вычисл.
f
при малых Р. Для прибл. вычисления
летучестей реал. газов можно воспользоваться
методом расчета, основ. на принципе
соответственных состояний
(ряд одинак. св-в, в том числе и коэфф.
акт-ти разл. реал. газов, оказываются
равными при одинак. приведенных
температурах ()
и приведенных давлениях ():
= Т/Ткр
,
= Р/Ркр
. Это дает возм-ть приближенно вычисл.
f
при малых Р. Для прибл. вычисления
летучестей реал. газов можно воспользоваться
методом расчета, основ. на принципе
соответственных состояний
(ряд одинак. св-в, в том числе и коэфф.
акт-ти разл. реал. газов, оказываются
равными при одинак. приведенных
температурах ()
и приведенных давлениях ():
= Т/Ткр
,
= Р/Ркр
|
есть универсальная функция и : = = (, ) . Эта закономерность – приближенная. На рис.: 2 1
|

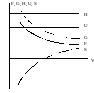
 lim
f/P=
1 при Р
0
(2). f
- функция, промежуточная м/у пар-рами
состояния газа Р и Т, с одной стороны,
и G
– с другой стороны. G
= G2
– G1
= RT
ln
f2
/
f1
при T=const.
Чтобы
вычисл. G
для –ц- с реал. газом, нужно
знать зав-ть f
от Р и Т.
Продифференцируем ур.(1) по Р при Т
=const
lim
f/P=
1 при Р
0
(2). f
- функция, промежуточная м/у пар-рами
состояния газа Р и Т, с одной стороны,
и G
– с другой стороны. G
= G2
– G1
= RT
ln
f2
/
f1
при T=const.
Чтобы
вычисл. G
для –ц- с реал. газом, нужно
знать зав-ть f
от Р и Т.
Продифференцируем ур.(1) по Р при Т
=const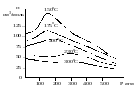
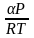 ,
=
= exp
(–
)
,
=
= exp
(–
)