Б.12.2.Осмос. Вывод уравнения для расчета осмотического давления.

Равновесие осущ-ся при рав-ве Т и Р во всех частях всех фаз в системе и при постоянстве состава во всех участках одной фазы. Если есть разности  компонентов м/у участками одной фазы или м/у разными фазами, эти компон. диффундируют в направлении падения своего  до тех пор, пока не будет достигнут одинак. состав во всех участках внутри каждой фазы и равновесное распределение компонентов м/у фазами. Необх. усл. достижения такого равновесия явл. возм-ть своб. перехода всех компонентов из 1 участка каждой фазы в др. участок и из 1 фазы в др. Иная картина, когда отд. части системы разделены перегородками, которые непроницаемы для одних компонентов и проницаемы для других (н-р, кожа, пергамент). Сосуд 1 содерж. водный р-р какого-либо в-ва; закрыт внизу полупрониц.

1 h 2

перегородкой. Сос.1 помещен в сос.2 с водой. Вода будет проходить из 2 в 1. Осмос – самопроизв. переход воды (или р-ля) ч/з полупроницаемую перегородку в р-р. Осмот. давление ()- сила (на ед. S), заставляющая р-ль переходить ч/з полупрониц. перегородку в р-р (наход. при том же внеш. Р, что и р-ль), Из-за осмоса уровень р-ра в сос. 1 повышается, создавая дополн. Р,

j препятствует осмосу. При нек. h столба жидк. в сос. 1 доп. Р достигает такой вел-ны, при j осмос прекращается (устанавлив. равновесие м/у р-ром данной конц. и чистым р-лем, разделёнными полупрониц. перегородкой). Равновесию м/у р-ром данной конц. и чистым р-лем соотв-ет определ. гидростатическое Р в сосуде с р-ром. Оно =  и отл. от него только знаком. Т.к. измеряемой вел-ной явл. гидростат. Р, то  можно определить как дополн. Р, j необх. приложить к р-ру, чтобы предотвратить поступление в него (или удаление из него) р-ля ч/з полупрониц. перегородку. Впервые  измерил Пфефер. Вант-Гофф показал, что в разб. р-рах зав-ть  от конц. совпадает по форме с з. Бойля-Мариотта для ид. газов. Для р-ров с с  0,3М V = 22,6 латм/моль (для ид. газов PV = 22,4 ; V – объем, закл. 1 моль раств. в-ва); при ↑ конц. ↑ V .   Т. Закономерности  разб. р-ров охватываются урав. Вант-Гоффа :  = cRT (с – моляр. конц.; с = (n₂/V) = g_2/(M₂V)) Т.о.,  разб. р-ров численно равно тому Р, j производило бы то же число молекул раств. в-ва, если бы оно в виде ид. газа занимало при данной Т объем, равный объему р-ра. Р-ль и р-р, разделенные полупрониц. перегородкой и нах-ся в равновесии, представляют 2 фазы, один из компонентов которых, свободно проходящий из одной фазы в другую, должен иметь в обеих фазах равные _. В чистом р-ле его ₁^о = const при Т, Р₁ = const (Р₁ – внешнее). В р-ре же его значение ₁ изм. с изм-ем N₁ и Р₂ (Р₂ = Р₁ +  – сумма первонач. Р и доп. гидростат. Р в р-ре, равного ). Это изменение можно найти, дифференцируя ₁ = ₁^о по N₁ и Р₂ , учитывая, что d₁^o = 0. d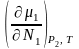₁ = dN₁ + 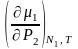dP₂ = d₁^o = 0; = 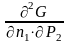= = 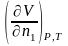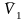_; ( Т.к. 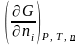_i = и 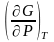= V )_; – обозначение частной производной по n_i; ₁ = ₁^o + RT ln a₁  = RT 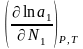;RT dN₁ + dP₂ = 0; dP₂ = – 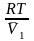dN₁ . Интегрируем, считая  const : 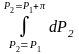= – 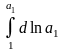(пределы интегрирования : нижний – чистый р-ль, верхний – р-р); Р₁ +  – Р₁ = – ln a_1; a₁ = P₁ / P₁^o ; P₁ и P₁^o – давл. нас. пара р-ля над р-ром и над чистым р-лем.  = – ln 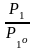(1)

Для ид. р-ров N₁ = P₁ / P₁^o (урав. Рауля): _ид = – ln N₁ = – ln (1 – N) (2)

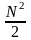Для разб. р-ров (N  1): – ln (1 – N) = N + + …  N ; N = 

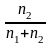
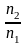
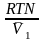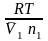
_разб = =  n₂

Если n₂  n₁ , то  n₁ = V (объему р-ра); n₂ /V = c₂ – моляльность. Получаем для разб. р-ров ур. Вант-Гоффа :

_разб = с₂RT = 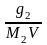RT (3)

Уравнение справедливо только для разб. р-ров, подчин. з. Рауля. При ↑ конц., даже если р-р идеален, урав. Вант-Гоффа неприменимо и заменяется урав. (2); в общем случае неид. р-ров справедливо лишь урав. (1). Р реал. газов в обычных условиях меньше Р ид. газов из-за влияния кохезионных сил (притяжения м/у молек. газа).  реал. р-ров знач. >  ид. р-ра.  явл. тем добав. Р, j увел.  р-ля в р-ре и этим компенсирует уменьш.  р-ля, вызванное растворением 2го компонента. Это создает возм-ть равновесия р-ра с чистым р-лем при наличии полупрониц. перегородки.