Б.19.1.Растворимость тв. В-в в жидкостях. Уравнен. Р-ти в ид. И пред. Разб. Р-рах. Откл. От ид. Р-ти.

Тв. в-во не может беспредельно растворяться в жидкостях: при достижении некоторой конц., определ. при данных Р и Т, тв. в-во перестает растворяться; устанавливается равновесие м/у р-ром и тв. в-вом. Насыщенный р-р – р-р, находящийся в равновесии с тв. в-вом, а его конц. – р-ть тв. в-ва.

Хим. потенциалы раствор. в-ва в насыщ. р-ре (_нас) и в тв. фазе (_т) имеют одно и то же значение :

_нас = _т ; ₂ = ₂^о + RT ln a₂ ; _{2, нас} = ₂^о + RT ln a_{2, нас} ; _{2, нас} – _т = ₂^о + RT ln a_{2, нас} – _т = 0

– RT ln a_{2, нас} = ₂^о – _т = G ; G = H + T – уравнение Гиббса-Гельмгольца

Растворение тв. в-ва в жидкости можно представить как 2 последовательно протекающих –ц- : 1) плавление тв. в-ва; 2) смешение 2х жидкостей. В случае ид. р-ров теплота 2-го процесса = 0. Теплота 1-го процесса – теплота плавления тв. в-ва Н_{2, пл} . Если при расчете а₂ в качестве станд. состояния 2-го компонента принята чист. жидкость, то ₂^о соотв. этому состоянию, а G = ₂^о – _т равно изменению G для плавления 1 моля чистого 2-го компонента при Т ниже Т плавления; соответственно Н = Н_{2, пл}

– RT ln a_{2, нас} = Н_{2, пл} + Т – R ln a_{2, нас} – RT 

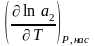
Н_{2, пл} = RT² ; =

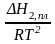
Для ид. р-ров : а₂ = N₂ = N d lnN = dT ; =

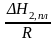
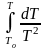
T_o – Т плавления 2-го компонента (N = 1); Т  Т_о lnN = – ( – 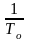) = – + B

(линейная зав-ть lnN от 1/Т). В это уравнение не вх. величины, характеризующие растворитель  идеальная растворимость вещества не зависит от природы растворителя. tg α = ∆H_{2, пл} / R

По вышеприведенному уравнению и по графику можно рассчитать Н2, пл; в случае идеальной р-ти (н-р, р-р нафталина в нитробензоле) она приблизительно равна экспериментально найденным другими методами Н2, пл .

Отклонения от ид. р-ти. Р-ть в реал. р-рах сильно отлич. от идеальной. В-ва сходной хим. природы часто имеют совершенно различные р-ти в том или ином р- ле. Современ. теоретические взгляды на взаимодействие компонентов в р-ре помогают качественно объяснить отдельные факты р-ти, но точно предсказывать величины р-ти какого-либо в-ва на основании данных для др. в-в пока невозможно. Общие закономерности ограничиваются качественными обобщениями, охватывающими лишь отд. классы р-ров. Известно, н-р, что неполярные в-ва лучше взаимно растворимы (так же, как и полярные), чем неполярное в-во в полярном растворителе и наоборот. Лишь для неполярных веществ (гл. образом, органических), р-ры которых обнаруживают небольш. полож. отклонения от з. Рауля, удается построить полуколичественную статистическую теорию растворимости. Сложное взаимодействие факторов, определяющих р-ть, приводит к тому, что в некот. случаях р-ть уменьшается с ↑ Т, тогда как кол-венные теории предсказывают ↑ раств-ти с Т.

Зав-ть р-ти тв. в-в от Р. Представление о малом влиянии Р на р-ть тв. тел в жидкостях справедливо лишь при небольших Р. В наст. время доступный для исследования диапазон Р расширился до десятков тысяч атмосфер и влияние Р на р-ть оказалось значительным.:

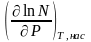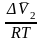= – – уравнение Планка – Ван-Лаара

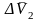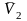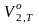= – – прирост объема при растворении 1 моля тв. в-ва в его насыщ. р-ре. Уравнение применимо к ид. и предельно разбавл. р-рам.