- •Б. 11. 1.Уравнения max работы Гиббса-Гельмгольца, их вывод и анализ.
- •Б.11.2.Активности компонентов раствора. 3 шкалы активности.
- •Б.12.1.Статистический хар-р 2 закона термодинамики. Ур. Больцмана, его вывод и анализ.
- •Б.12.2.Осмос. Вывод уравнения для расчета осмотического давления.
- •Б. 13.1.Термодин. Потенциалы идеальных и реал. Газов. Летучесть реал. Газа и ее расчет.
- •Б.13.2. Гетерог. Равновесия. Составл. В-ва системы, комп-ты, фазы, степ. Свободы. Правило фаз.
- •Б.14.1.Фаз. Переходы I рода для индив. В-в. Урав. Клапейрона-Клаузиуса. Фаз. Переходы II рода.
- •Б.14.2. Диаграммы состояния воды, серы, бензофенона.
- •Диаграмма состояния серы
- •Б. 15.1. Уравн. Для характер. Функций многокомпон. Систем, . Урав. Гиббса-Дюгема.
- •Б.15.2. Условия хим. Равновесия. Здм (вывод, анализ). Разл. Формы выражения к равн.
- •Б.16.1.Давление нас. Пара бинарных р-ров. Закон Рауля. Ид. Растворы. Предельно разбавл. Р-ры.
- •Б.16.2. Влияние т на хим. Равновесие. Уравн. Изохоры и изобары –ц-, их вывод, анализ, интегр-е.
- •Б. 17.1.Отклонения от законов идеальных растворов, причины отклонений.
- •Диаграмма сост. Системы, образ. Хим. Соединение, плавящееся инконгруентно (с разложением).
- •Б.18.1.Огр. Взаим. Р-ть жидкостей. Р-ть газов в жидкостях. З. Генри, Дальтона, Сеченова. Влияние t0.
- •Б.18.2.Трехкомпонентные системы. Способы изобр. Состава. Диаграмма с тройной эвтектикой.
- •Б.19.1.Растворимость тв. В-в в жидкостях. Уравнен. Р-ти в ид. И пред. Разб. Р-рах. Откл. От ид. Р-ти.
- •Б.19.2. Диаграмма состояния 2хкомпонентной системы с неогр. Взаимной р-тью компонентов.
Б.16.2. Влияние т на хим. Равновесие. Уравн. Изохоры и изобары –ц-, их вывод, анализ, интегр-е.
В соответствии с принципом подвижного равновесия можно установить кач-венное правило смещения хим. равновесия с изм. Т. При ↑ температуры Т смещение равновесия должно сопровождаться увелич. S; т.к. (Т)Р (S)Т 0, то хим. равновесие при ↑ Т должно сместиться в сторону эндотерм. реакции, а при ↓ Т – в том направлении, в j протекает экзотерм. реакция. Выражение для кол-венной зав-ти хим. равновесия от Т можно получить из 2х ур.: 1) урав. изотермы реакции Вант-Гоффа для изобар. потенциала хим. реакции: G = – RT ln KP + RT i ln Pi (1) (Pi – исход. парц. Р; постоянны) 2) уравн. max работы Гиббса-Гельмгольца : G = H + T (2)
Подставим
(1) в
:
= – R
ln
KP
– RT
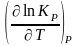 + R
i
ln
Pi
+ R
i
ln
Pi
G
= H
– RT ln
KP
– RT2
+ RT
i
ln
Pi
сокращаем
, = (1)
=
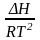
P
= const
:
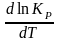 =
= –
=
= –
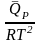 – урав.
изобары хим. реакции Вант-Гоффа
– урав.
изобары хим. реакции Вант-Гоффа
Аналогично из F = – RT ln KC + RT i ln Ci и F = U + T получаем
урав. изохоры
хим. реакции Вант-Гоффа
:V
= const
:
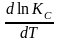 =
=
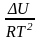 = –
= –
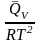
Эти уравнения в дифф. форме показыв. зав-ть К равн. в смеси ид. газов от Т. Если реакция протекает в смеси реал. газов, то КР заменяется на Кf ; КС – на Ка , если реакция протекает в неид. р-ре.
Эти уравн. позвол. предвидеть зав-сть Кр от Т : если Н 0, то 0, т.е. КР растет с ростом Т.
Если интервал
Т небольшой, то H
= const.
d
ln
KP
=
dT
; ln
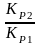 =
=
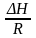
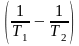 =
=
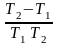
lg
=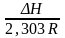
Если знаем Н
и КР1
(КР2),
то можно рассч. КР2
(КР1)
Если знаем Н
и КР1
(КР2),
то можно рассч. КР2
(КР1)
(экзотерм.)
) (эндотерм.) H 0 1/T |
ln
KP
= –
HT
= Ho
+
|
СР
= a
+ bT
+
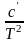 или
СР
= a
+ bT
+ cT2
+ dT3
HT
= Ho
+ aT
+ bT2
+ cT3
+ …
или
СР
= a
+ bT
+ cT2
+ dT3
HT
= Ho
+ aT
+ bT2
+ cT3
+ …
d
ln
KP
=
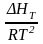 dT
=
dT
=
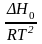 dT
+
dT
+
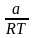 dT
+
dT
+
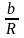 dT
+
dT
+
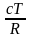 dT
+ …
dT
+ …
ln
KP
= –
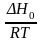 +
+
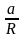 lnT
+
T
+
lnT
+
T
+
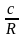 T2
+ … + const
T2
+ … + const
Чтобы найти const, нужно знать экспериментально определить КР для одной Т. Gо = RT ln KP
(Gо станд. изобар. потенц. реакции – если Рi = 1 – парц. Р всех участников реакции в исх. смеси)
G = H – TS , GTo = HTo – TSTo (о означает, что величины станд.; Т – любая)
RT
ln
KP
= HTo
– TSTo
при
Т
= const
ln
KP
= –
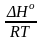 +
+
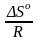 (2)
(2)
Сравнение ур.
(1) и (2) для ln
KP
показывает, что Н
= Но
в урав. изобары хим. реакции; tg
= – Ho/R
; const
= So/R
.
=
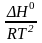 – уравнение
изобары
– уравнение
изобары

 ln
KP
H
0
ln
KP
H
0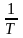 + const
(1) ; tg
= –
+ const
(1) ; tg
= –
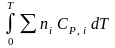 (Ho
– пост. интегрирования уравненияя
Кирхгоффа и не имеет физ. значения
теплоты реакции при Т = 0) или HT2
= HТ1
+
(Ho
– пост. интегрирования уравненияя
Кирхгоффа и не имеет физ. значения
теплоты реакции при Т = 0) или HT2
= HТ1
+