Б.16.1.Давление нас. Пара бинарных р-ров. Закон Рауля. Ид. Растворы. Предельно разбавл. Р-ры.

Насыщ. пар содержит, в общ. случае, все компоненты р-ра, и Р насыщ. пара =  парц. Р компонентов. Но часто отд. компоненты нелетучи при данной Т и отсут. в газ. фазе. Полное Р нас. пара и парц. Р явл. функциями Т и состава р-ра. При Т = const состояние бин. р-ра определ-ся лишь конц.1 из компонентов. Диаграмма Р – состав для р-ра 2х жидкостей, смешивающихся во всех

Р РоВ Р = РА + РВ РоА РВ РА А В

отношениях. РоА и РоВ – Р пара чистых жидкостей. Состав насыщ. пара определяется мольной долей 2-го компонента: N2 = Р2 / Р (Р2 – парц. давление 2-го компонента, Р – полное давление пара). Если насыщ. пар - ид. газ, то для компонентов пара: i = Gi (T) + RT ln pi ; 2 = G2 (T) + RT ln p2 Т.к. хим. потенциалы компонента в равновесных фазах равны, то это уравнение имеет силу и для жидкого раствора. Для чистого жидкого 2-го компонента при той же Т: о2 = Gо2 (T) + RT ln Ро2 ; Получаем: 2 = о2 (T) + RT ln (p2 / p20)

При высоких Т и Р нас. пар р-ра не явл. ид. газом: ₂ = ^о₂ (T) + RT ln (f₂ / f₂⁰); f₂ – парциальная летучесть 2-го компонента в р-ре; f ^o₂ – летучесть 2го компон. в виде чистой жидкости при той же Т.

ЗАКОН РАУЛЯ. В простейшем случае зав-ть парц. Р пара р-ля от состава бинарного р-ра:

Р₁ = Р^о₁ N₁ = P^o₁ (1 – N₂ ) = P^o₁ (1 – N) Т.е. изображается на диаграмме P – N прямой линией.

З. Рауля : относительное понижение парц. Р пара р-ля = N раствор. в-ва N = ( P₁⁰ – P₁) / P₁⁰ (1)

Закон применим к р-рам, нас. пар j ведет себя как ид. газ. Немногие р-ры подчиняются этому закону. Пока Р нас. пара невелико, отклонения от з. Рауля малы. При высоких Т, когда Р нас. пара велико, термодинам. св-ва газов нужно связывать с летучестями и з. Рауля выражать в след. форме:

f₁ = f ^о₁ N₁ = f ^o₁ (1 – N ) ; N = 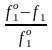(2)

Р-ры, следующие з. Рауля в форме урав. (2) при всех конц. и всех Т, наз-ся идеальными (совершенными) р-рами; это предельный, простейший тип жидких р-ров. Для пара раствор. в-ва должно соблюд. урав., аналогичное вышеприведенному. Из уравнений (2) получаем:

d f₁ = f ^o₁ d (1 – N ) = – f ^o₁ dN и подставляем в уравнение Дюгема-Маргулеса:

d ln f₂ = – d ln f₁ = – 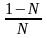d ln f₁ = – = =

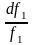d ln f₂ = ; ln f₂ = ln N + ln k ; f₂ = kN (3) Если р-р ид., то (3) справедливо для всех конц.

При N =1 f₂ = k = f ^o₂ ; f₂ = f ^o₂ N. В неид. р-рах k  f ^o₂ Для многокомп. ид. р-ра: f_i = f ^o_i N_i (4)

При невысоких Т, когда парциальные давления компонентов невелики и летучести компонентов близки к их парциальным давлениям, возвращаемся к закону Рауля в форме уравнения (1), а уравнение (3) приобретает вид: Р₂ = kN – з. Генри: парц. Р пара раствор. в-ва пропорционально его N. k – коэф. Генри. В ид. р-ре при малых Р нас. пара, когда f₂ = P₂, k = P^o₂ и P₂ = P ^o₂ N (6)

В общем виде для многокомпонентного ид. р-ра при невысоких Р: P_i = P ^o_i N_i (7)

Р1 = Po1 (1 – N) P2 = P o2 N

Эти 2 урав. отражают св-ва парц. давлений ид. р-ров при малых Р. (объединенный з. Рауля-Генри).

Полное Р пара ид. бинарного р-ра: Р = Р₁ + Р₂ = Р^о₁ – (Р^о₁ – Р^о₂ )N ; Р – линейная функция N.

Примеры ид. р-ров : дибромпропан – дибромэтан, бензол – толуол, гексан – октан.

В общ. случае составы ид. р-ра и его насыщ. пара не совпадают: N = =

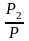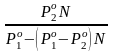
N – конц. 2-го компонента в паре; N = N при всех конц. только в том случае, если Р^о₁ = Р^о₂.

Для хим. потенциала компонента р-ра: ₂ = ^о₂ (T) + RT ln (P₂/P₂⁰) ; ₂ = ^о₂ (T) + RT ln ( f₂ / f₂⁰ )

Учитывая (из ур. (7) и (4)), что P_i / P^o_i = N_i , f_i / f ^o_i = N_i , получаем урав. для хим. потенциала компонента ид. жидк. р-ра, совпадающее по форме с урав. для _i ид. газ. смеси: _i = ^о_i (T) + RT ln N_i

Часто Р пара р-ля при малых конц. остальных компонентов следуют з. Рауля и в р-рах, не явл. ид., т.е. в сильно разбавл. р-рах. Для них Р₁=P^o₁ (1 – N) и одновременно P₂ = kN , где k  Р ^o₂. Такие р-ры - предельно разбавленные. При образовании ид. р-ров из чистых жидких компонентов Q не погл. и не выдел., а V р-ра = сумме объемов жидких компонентов.