Б.15.2. Условия хим. Равновесия. Здм (вывод, анализ). Разл. Формы выражения к равн.

Хим. реакции обратимы : наряду с хим. взаимодействием м/у исх. в-вами (прямая реакция) протекает хим. взаимодействие м/у продуктами реакции (обратная реакция), в рез. которого снова образ. исх. в-ва. По мере протекания -ц- скорость прямой реакции (кол-во молекул, прореагировавших за секунду) уменьшается, а скорость обратной реакции увел.. Когда обе скорости сравняются, наступает состояние хим. равновесия  число молекул в-в, составляющих хим. систему, перестает меняться и остается постоян. во времени при неизменных внеш. усл.. Хим. равновесие явл. динамичным и подвижным  с изменен. внешн. условий равновесие сдвигается в одну или в др. сторону; б/м изменение внешн. условий влечет за собой б/м изменение состояния равновесия. Т.о., хим. реакции могут протекать как равновесные –ц-, т.е. к ним можно применять общие условия термодинамич. равновесия.

Изменение G системы, в j протек. хим. реакция: dG =  SdT + VdP + ₁dn₁ + ₂dn₂ + ...

Однако в этом случае изменения масс компонентов dn₁, dn₂ ... не являются независимыми, а связаны стехиометрическими соотношениями : ₁А₁ + ₂А₂ + ... = ₁А₁ + ₂А₂ + ...

Изменения масс компонентов, выраженные в молях, пропорциональны стехиомет. коэф. уравнения реакции, взятым с соответств. знаком («» для исчезающих в-в, «+»  для образ.) :

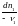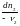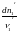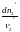= = ... = = = ... = d

изменения масс исх. в-в изменения масс продуктов реакции

Отношение dn_i/_i одинаково для всех участников хим. реакции и м.б. записано в форме дифференциала некоторой величины .   хим. переменная : показывает m каждого компонента, вступившую к данному моменту в реакцию и измеренную в эквивалентных единицах, отвечающих уравнению реакции.  характеризует только одну определ. хим. реакцию. Если в системе протекает несколько реакций, то для каждой из них имеется своя переменная (₁ , ₂ ...).

dG = VdP  SdT  ₁₁d  ₂₂d  ... + ₁₁d + ₂₂d + ... =

= VdP  SdT + (_i_i)d

Здесь G = G (P, T, 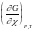) , = _i_i

Част. произв. G по  =алгеб.  произведений _i_i . При P,T = const : (G)_P,T = (_i_i)d

Для реакций, протекающих самопроизв. при P,T = const , dG  0  (_i_i)  0 , т.к. d  0. Когда реакция находится в состоянии равновесия, функция G = f () имеет min значение :

= _i _i = 0  условие хим. равновесия (в общей форме). Аналогично:

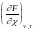= _i_i = 0 в состоянии равновесия.

ЗДМ. Связь м/у равновесными концентрациями (или парц. давлениями) в-в, участвующих в хим. реакции, выражается ЗДМ, кол-венная формулировка и вывод были даны Гульдбергом и Вааге (1867).

₁А₁ + ₂А₂  ₁А₁ + ₂А₂

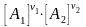
v₁ = k₁  скорость прямой реакции

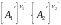
v₂ = k₂  скорость обратной реакции

v₁ = v₂ в состоянии равновесия

k₁ = k₂

К_С = k₁ / k₂ = /

(К_С  константа равновесия, выраженная через концентрации)

ЗДМ можно вывести из урав. _i_i = 0 , если химические потенциалы выразить как функции концентраций, парциальных давлений и т.д. компонентов, участвующих в реакции :

_i = G_i (T) + RT ln C_i

_i = G_i(T) + RT ln P_i  если компоненты  идеальные газы

_i = G_i(T,P) + RT ln N_i

_i = _i (T) + RT ln f_i  если компоненты  реальные газы

_i = _i^o (T) + RT ln N_i  если компоненты  идеальные растворы

_i = _i^o (T) + RT ln a_i  если компоненты  реальные растворы

Выведем ЗДМ для газовой реакции, если компоненты  идеальные газы. Исходное уравнение _i = G_i(T) + RT ln P_i подставим в уравнение _i_i = 0.

_i G_i(T) + RT _i ln р_{i, равн} = 0

_i ln р_{i, равн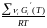} =  = f (T)

Опустим индекс (равн); заменим сумму логарифмов логарифмом произведения р_i ; а f (T)  логарифмом некоторой функции К_Р (Т) :

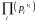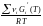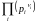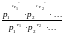ln =  = ln K_P (T)

= = K_P (T)

Величина К_Р, выраженная ч/з равновесные парц. давления в ид. газовой смеси, есть функция только Т и не зав. от суммарного Р и парц. давлений компонентов в исх. смеси. При T = const K_P = const. К_Р  константа хим. равновесия , а уравнение - закон действия масс.

Если газ  реал., то таким же путем получим : K_f = 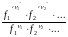; K_f  K_P при Р  0

В применении к конкр. хим. реакции: N₂ + 3H₂  2NH₃

K_P = 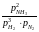; K_f =

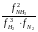
Вид выражения для К_Р и ее числ. значение зав. от того, в каком направлении и для каких кол-в записано стехиометрическое уравнение реакции :

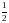N₂ + 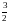H₂  NH₃ 2NH₃  N₂ + 3H₂

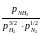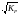К_Р = = К_Р = =

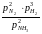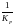
Необх. различать Кр, выраженные разн. способами, т.к. их числ. значения разные.

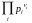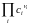K_P = ; K_C = ; K_N =

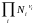
Связь м/у ними можно установить, используя уравнения для ид. газовой смеси : P_i = C_iRT  K_P = K_C (RT)^ P_i = N_iP  K_P = K_N P^

 = ₁ + ₂ + ₃ + ...  ₁  ₂  ₃  ...

Т.к. К_Р не зависит от Р (для ид. газов), то и К_С от него не зависит. K_N же зависит от Р и не зав. от исх. кол-в компонентов. Если  = 0, т.е. реакция протекает без изменения числа молекул, то К_Р = К_С = К_N .