
- •Б. 11. 1.Уравнения max работы Гиббса-Гельмгольца, их вывод и анализ.
- •Б.11.2.Активности компонентов раствора. 3 шкалы активности.
- •Б.12.1.Статистический хар-р 2 закона термодинамики. Ур. Больцмана, его вывод и анализ.
- •Б.12.2.Осмос. Вывод уравнения для расчета осмотического давления.
- •Б. 13.1.Термодин. Потенциалы идеальных и реал. Газов. Летучесть реал. Газа и ее расчет.
- •Б.13.2. Гетерог. Равновесия. Составл. В-ва системы, комп-ты, фазы, степ. Свободы. Правило фаз.
- •Б.14.1.Фаз. Переходы I рода для индив. В-в. Урав. Клапейрона-Клаузиуса. Фаз. Переходы II рода.
- •Б.14.2. Диаграммы состояния воды, серы, бензофенона.
- •Диаграмма состояния серы
- •Б. 15.1. Уравн. Для характер. Функций многокомпон. Систем, . Урав. Гиббса-Дюгема.
- •Б.15.2. Условия хим. Равновесия. Здм (вывод, анализ). Разл. Формы выражения к равн.
- •Б.16.1.Давление нас. Пара бинарных р-ров. Закон Рауля. Ид. Растворы. Предельно разбавл. Р-ры.
- •Б.16.2. Влияние т на хим. Равновесие. Уравн. Изохоры и изобары –ц-, их вывод, анализ, интегр-е.
- •Б. 17.1.Отклонения от законов идеальных растворов, причины отклонений.
- •Диаграмма сост. Системы, образ. Хим. Соединение, плавящееся инконгруентно (с разложением).
- •Б.18.1.Огр. Взаим. Р-ть жидкостей. Р-ть газов в жидкостях. З. Генри, Дальтона, Сеченова. Влияние t0.
- •Б.18.2.Трехкомпонентные системы. Способы изобр. Состава. Диаграмма с тройной эвтектикой.
- •Б.19.1.Растворимость тв. В-в в жидкостях. Уравнен. Р-ти в ид. И пред. Разб. Р-рах. Откл. От ид. Р-ти.
- •Б.19.2. Диаграмма состояния 2хкомпонентной системы с неогр. Взаимной р-тью компонентов.
Б. 11. 1.Уравнения max работы Гиббса-Гельмгольца, их вывод и анализ.
Св-ва функций F и G дают возм-ть установить связь м/у max работой равновесн. –ц- и теплотой того же процесса, но протек. неравновесно.
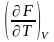 =
– S,
F
= U
– TS,
F
= U
+ T
=
– S,
F
= U
– TS,
F
= U
+ T
Запишем это урав. для 2х состояний системы:
F1
= U1
+ T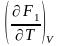 , F2
= U2
+ T
, F2
= U2
+ T ,
,
F1
– F2
= U1
– U2
+ T
 (F1
– F2)V
= – F
(F1
– F2)V
= – F
Amax
=
 + T
+ T
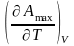 (1)
(1)
Зная Amax (или F) и зависимость ее от Т, можно вычисл. теплоту –ц- (т.е. U). Если же известна Q –ц-, то для расчета Amax необх. интегрировать (1), причем появл-ся const интегрирования,для опр-я кот. необходимы доп. сведения. Урав. (1) – урав. Amax (уравнение Гиббса-Гельмгольца) – может быть записано и в форме:
F
= U
+ T
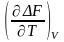 (2)
Др.варианты уравнения Гиббса-Гельмгольца:
(2)
Др.варианты уравнения Гиббса-Гельмгольца:
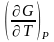 =
– S , G = H – TS , G = H + T
;
=
– S , G = H – TS , G = H + T
;
G1
= H1
+ T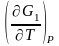 , G2
= H2
+ T
, G2
= H2
+ T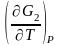 ;
;
G1 – G2 = H1 – H2 + T (G1 – G2)P ;
Amax
=
 + T
+ T
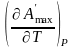 (3)
G
= H
+ T
(3)
G
= H
+ T
 (4)
(4)
U = QV и H = QP справедливы,если в 1-м случае А = 0, а во 2-м соверш. только А расширения (А=0).Поэтому в (1) и (3) и отн-ся не к –ц-,которым соответствуют А или А,а к –ц-,протекающим м/у теми же нач. и кон. состояниями,но без совер.работы (для QV) или с совер.только А расширения(для QP),т.е. в неравновесных условиях.Теплоты же равновесного –ц-,равные ТS, выраж. послед. членами уравнений (1) и (3). Уравнения можно записать так:
– F = Amax = – QV, неравн + QV, равн ;
– G = Amax = – QP, неравн + QP, равн
Б.11.2.Активности компонентов раствора. 3 шкалы активности.
Ур-е для хим.потенц.компонентов реал. р-ра :(1) i = iо (T) + RT ln (Pi / Pio) пар – ид. газ; (2) i = iо (T) + RT ln (fi /fio) пар – реал. газ.Ур-е для хим.потенц.компонента в ид.р-ре:(3) i = iо (T) + RT ln Ni.Отношение Pi / Pio (или fi /fio ) играет такую же роль в ур.для реал.р-ра,что и мол. доля Ni в ур-ии для ид.р-ра.Это отношение наз-ся термодинам. активностью компонента р-ра(или активностью компонента): ai = Pi / Pio ; ai = fi /fio
(4) i = iо (T) + RT ln ai – выр-е для хим.потенц.любого неид.р-ра.Используя его,можно для любого реал.р-ра получить термодинам.ур-я,j будут иметь тот же вид,что и ур-е для ид.р-ра,но вместо Ni – ai .При наличии разных значений компонента в разл.частях изотерм. системы компонент переходит(путем диффузии и др.)из части системы с большим знач. в часть с меньшим значением.В ид.р-рах компонент самопроизв.переходит от части р-ра с большей конц.этого компонента в часть с меньшей;в реал.р-рах компонент переходит в направлении меньших величин ai .При равновесии эти величины=во всех частях р-ра в одном р-ле,м/у j возможно своб.перемещение компонента.В соот(1)и(2)термодинам.хар-кой компонента р-ра м.б.его парц.давл.Pi или летучесть fi в насыщ.паре над р-ром.Но эти величины для малолетучих компонентов практически неопределимы,тогда как ai м.б.определена не только из ур-й,но и др.методами.Метод активности – формальный прием,закл.во введении новой ф-ии состояния,промежуточной м/у хим.потенц.и конц-ей.Он ничего не дает для понимания причин отклонения дан.р-ра от закона ид.р-ров.Но он упрощает матем.разработку термодинамики р-ров. аi – отн. летучесть ( или отн. давление пара),т.е.отношение летучести при дан.условиях к летучести в известном станд.состоянии.Для станд.состояния летучесть равна fio и ai =1 1.Станд. состояние – чистый жидкий компонент при той же Т.Но часто приходится выбирать иные станд.состояния,т.к. большое число в-в в широком интервале Т сущ.в тв.состоянии и давления насыщ.пара компонента часто ничтожно малы в опытных условиях. Изотермы ai – Ni для бинарных смесей :
Идеальный раствор ai = Ni (дибромпропан-дибромэтан) |
Полож. отклонение от з. Рауля ai Ni (бензол-ацетон) |
|
Коэф.активности компонента i - мера откл.св-в р-ра от св-в ид.р-ра той же конц.
i
=
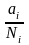 =
=
 =
=
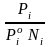
Для ид. р-ров i = 1 ;в случ.полож.отклонений Рi PioNi и i 1;в случ.отриц.отклонений Рi PioNi и i 1.В предельно разб.р-рах коэфф-ты активности р-ля и раств.в-в=1,если правильно выбраны станд.состояния.
Возможно сопоставление акт-ей компонентов с конц., выраж. не только в Ni:
1)Мольные доли (N): aN = N; – рациональный коэф. активности ; aN N при N 0 ; aN = N ( указ. на пред.разб.р-р) 2)Мольно-объемная концентрация (молярность с) : aC = f c; f – мольный коэф. акт-ти; aC c при с 0 ; аС = с 3)Моляльность (m): am = m; – практический (моляльный) коэф. акт-ти; am m при m 0; am = m. широко исп-ся в применении к электролитам;f используется реже.В конц. р-рах все коэф.акт-ти разл. по величине.В разб.р-рах,где N,c,m пропорциональны др.др,коэф. , f, равны.

 1
1
1
1

