6 Билет

1. Вектор. Понятия

Ответ: в геометрическом смысле вектор — это направленный отрезок, обычно определяемый точками своего начала и конца. Так или иначе вектором - называется отрезок, имеющий определенную длину и направление

Основные понятия

1) Модулем вектора |a| в геометрии называется его длина

2) Коллинеарными называются такие вектора, векторное произведение которых равно нулю. Это параллельные вектора. Коллинеарные вектора могут быть сонаправленными или встречными, то есть направленными строго в противоположные стороны.

3) Ортогональными (перпендикулярными) называются такие вектора, скалярное произведение которых равно нулю. Для любого вектора все вектора, лежащие в любой перпендикулярной ему плоскости, будут ортогональны.

4) Нулевым является вектор, имеющий нулевую длину, то есть тот, у которого координаты начала и конца строго совпадают. В связи с этим обычно нельзя говорить о направлении такого вектора, поэтому его считают не имеющим направления.

5) Компланарными называются вектора, которые приведены к одному началу и лежат в одной плоскости. Если хотя бы один из 3 векторов – нулевой, то три вектора тоже компланарны.

6) Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.

7) Косинус угла между векторами равен скалярному произведению векторов, поделенному на произведение модулей векторов.

2. Сумма векторов и произведение вектора на число.

Ответ: начнем с простого, чтобы сложить два вектора, достаточно сложить каждую из его координат. Т.е. если есть два вектора с координатами: a (x y z) u b (x1 y1 z1) то их суммой будет:

(x+x1;y+y1;z+z1). С этим ясно, умножение вектора на число тоже довольно просто. Если есть вектор a(x y z) и число b=4, то просто домножаем КАЖДУЮ координату на это число.

3. Условие коллинеарности векторов:

Ответ:

1) Два вектора коллинеарны, если их отношения равны

2) Два вектора коллинеарны, если их векторное пр-е равно нулю.

Пример внизу.

4. Свойства линейных операций над векторами

Сложение векторов коммутативно:  .

Сложение векторов ассоциативно:  .

Прибавление нулевого вектора к любому не меняет последнего:  .

Для любого вектора   существует вектор   такой, что   или  .

Умножение вектора на число ассоциативно:  . Умножение вектора на число дистрибутивно относительно сложения чисел:  .

Дистрибутивность умножения векторов относительно сложения

Умножение вектора на число дистрибутивно относительно сложения векторов:  .

Очевидно, умножение на единицу не меняет вектор:  .

Билет 7

1. Базис и система координат на плоскости и в пр-ве

Ответ: Базисом плоскости называется пара линейно независимых (неколлинеарных) векторов  , взятых в определённом порядке, при этом любой вектор плоскости является линейной комбинацией базисных векторов.

Любой вектор плоскости   единственным образом раскладывается по базису  : , где   – действительные числа. Числа   называют координатами вектора в данном базисе.

Также говорят, что вектор   представлен в виде линейной комбинации базисных векторов. То есть, выражение   называют разложением вектора   по азису   или линейной комбинацией базисных векторов.

Иными словами, говоря о разложении по базису мы подразумеваем какие-то коэффициенты, которые соответствуют векторам.

1.1 Система координат на плоскости

Ответ: Когда говорят о прямоугольной системе координат, то чаще всего имеют в виду начало координат, координатные оси и размерность по осям. Прямоугольную систему координат вполне можно определить через ортонормированный базис  . И это почти так. Формулировка звучит следующим образом:

Точка   плоскости, которая называется началом координат, и ортонормированный базис  задают декартову прямоугольную систему координат плоскости. То есть,  прямоугольная система координат однозначно определяется единственной точкой и двумя единичными ортогональными векторами  .

Думаю, всем понятно, что с помощью точки   (начала координат) и ортонормированного базиса   ЛЮБОЙ ТОЧКЕ плоскости и ЛЮБОМУ ВЕКТОРУ плоскости можно присвоить координаты. Образно говоря, «на плоскости всё можно пронумеровать».

Обязаны ли координатные векторы быть единичными? Нет, они могут иметь произвольную ненулевую длину. Рассмотрим точку    и два ортогональных вектора   произвольной ненулевой длины. Собственно пример данной системы, всем известной:

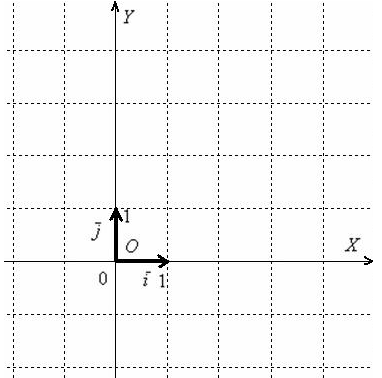
1.2. Система координат в пр-ве

Ответ: Базисом трёхмерного пространства называется тройка линейно независимых (некомпланарных) векторов  , взятых в определённом порядке, при этом любой вектор пространства единственным образом раскладывается по данному базису  , где   – координаты вектора   в данном базисе

Напоминаю, также можно сказать, что вектор   представлен в виде линейной комбинации базисных векторов.

Понятие системы координат вводится точно так же, как и для плоского случая, достаточно одной точки и любых трёх линейно независимых векторов:

Точка   пространства, которая называется началом координат, и  некомпланарны евекторы  , взятые в определённом порядке,  задают аффинную систему координат трёхмерного пространства:

Точка   пространства, которая называется началом координат, и ортонормированныйбазис   задают декартову прямоугольную систему координат пространства.:

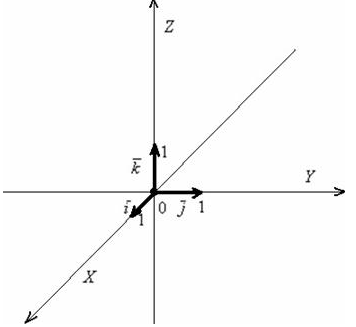
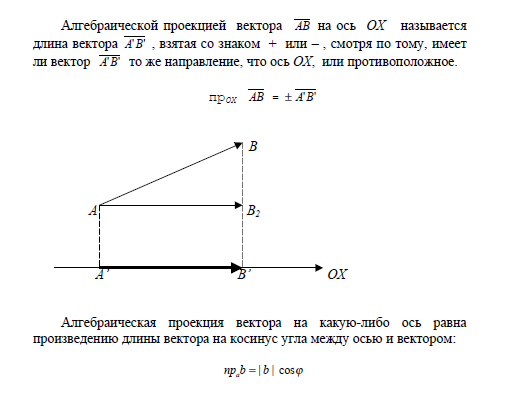
2. Геометрические и алгебраические проекции вектора на ось

3. Координаты вектора на плоскости и в пространстве

Начну с векторов на плоскости. Изображаем декартову с.к. и откладываем единичные вектора.

Векторы   и   ортогональны. Ортогональны = Перпендикулярны.

Обозначение: ортогональность векторов записывают привычным значком перпендикулярности, например:  .

Рассматриваемые векторы называют координатными векторами или ортами. Данные векторы образуют базис на плоскости. Иногда построенный базис называют ортонормированным базисом плоскости: «орто» – потому что координатные векторы ортогональны, прилагательное «нормированный» означает единичный, т.е. длины векторов базиса равны единице.

Обозначение: базис обычно записывают в круглых скобках, внутри которых в строгой последовательности перечисляются базисные векторы, например:  . Координатные векторы нельзя переставлять местами.

Ответ: Любой вектор   плоскости единственным образом выражается в виде: , где   – числа, которые называются координатами вектора в данном базисе. А само выражение   называется разложением вектора   по базису  .

Координаты на плоскости.

Теперь рассмотрим векторы в трехмерном пространстве, здесь практически всё так же, только добавится ещё одна координата. 

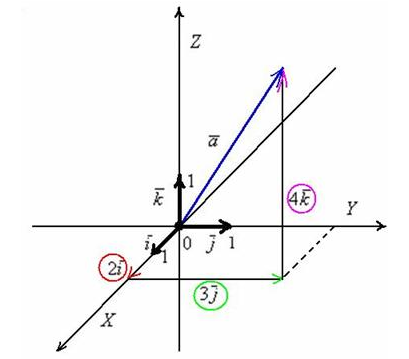
Это есть ортонормированный базис   трехмерного пространства и прямоугольная система координат, единичные векторы   данного базиса попарно ортогональны:   и  . Ось   наклонена под углом 45 градусов только для того, чтобы складывалось визуальное впечатление пространства. И в данном случае координаты отдельных векторов будут записывать в соответствии с i j k, и вместо отсутствующих координат будут ставить нули. Например 3j – коорд. Y => вектор b (0 3 0).

Билет 8

1. Направляющие косинусы вектора

Ответ: это косинусы углов, которые вектор образует с положительными полуосями координат. Направляющие косинусы однозначно задают направление вектора. Если вектор имеет длину 1, то его направляющие косинусы равны его координатам. Следовательно вывод: направление вектора в пространстве определяется углами , которые вектор образует с осями Косинусы этих углов называются направляющими косинусами вектора:  ,  ,  .

С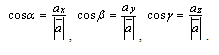 вязь между ними: Это обязательное условие!

А находят их так:

Далее, это орт, он же единичный вектор который находится ТОЧНО так же, как и направляющие косинусы, разве что вместо cos пишем v с галочкой наверху.

2. Сумму векторов и произведение вектора на число находили выше, хуй знает почему в этом билете тот же вопрос.

Билет 9

Ответ: 1. Нахождение координат вектора, зная начало и конец + координаты середины:

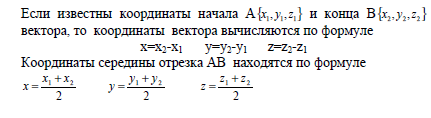
2. Расстояние между двумя точками:

3. Деление в заданном отношении

Очень простой вопрос, но тем не менее:

Билет 10

Билет 11

Три некомпланарных вектора a, b и с, взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора с кратчайший поворот от первого вектора а ко второму вектору b виден совершающимся против часовой стрелки, и левую, если по часовой (см. рис. 16).

      

 Векторным произведением вектора а на вектор b называется вектор с, который:

1. Перпендикулярен векторам a и b, т. е. с^а и с^b;

2. Имеет длину, численно равную площади параллелограмма, построенного на векторах а иb как на сторонах (см. рис. 17), т. е. 

3.Векторы a, b и с образуют правую тройку.

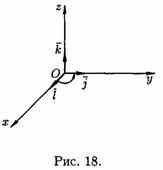
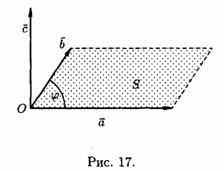
Геометрический смысл векторного произведения: модуль векторного произведения векторов численно равен площади параллелограмма, построенного на этих векторах как на сторонах.

Векторное произведение обозначается а х b или [а,b].

Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными.

Условия коллинеарности векторов

• Два вектора коллинеарные, если отношения их координат равны.

• Два вектора коллинеарные, если их векторное произведение равно нулю.

Алгебраические свойства векторного произведения

Для любых векторов  ,  ,   и любого действительного числа  :

1.  ;

2.  ;

3.  .

Первое свойство определяет антисимметричность векторного произведения, второе и третье — аддитивность и однородность по первому множителю. Эти свойства аналогичны свойствам произведения чисел: первое свойство "противоположно" закону коммутативности умножения чисел (закон антикоммутативности), второе свойство соответствует закону дистрибутивности умножения чисел по отношению к сложению, третье — закону ассоциативности умножения. Поэтому рассматриваемая операция и называется произведением векторов. Поскольку ее результатом является вектор, то такое произведение векторов называется векторным.

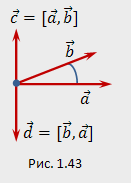
Докажем первое свойство, предполагая, что векторы   и   не коллинеарны (в противном случае обе части доказываемого равенства равны нулевому вектору). По определению векторы   и   имеют равные длины   и коллинеарны (так как оба вектора перпендикулярны одной плоскости). По определению тройки векторов   и   — правые, т.е. вектор   направлен так, что кратчайший поворот от   к   происходит в положительном направлении (против часовой стрелки), если смотреть из конца вектора  , а вектор   направлен так, что кратчайший поворот от   к   происходит в положительном направлении, если смотреть из конца вектора   (рис. 1.43). Это означает, что векторы   и   противоположно направлены. Следовательно,  , что и требовалось доказать. Доказательство остальных свойств приведено ниже (см. пункт 1 замечаний 1.13).

Координаты вектора с находим с помощью определителя матрицы:

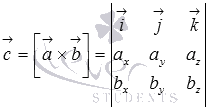
Рассчитываем определитель, приводим подобные, коэффициенты при I,J,k и будут координатами x, y, z соответственно .

Билет 12

Билет 13

Множество L  называется линейным или векторным пространством, если для всех элементов (векторов) этого множества определены операции сложения и умножения на число и справедливо:

1. Каждой паре элементов x и y из L отвечает элемент x + y из L, называемый суммой x и y, причём:

x + y = y + x − сложение коммутативно;

x + (y + z) = (x + y) + z − сложение ассоциативно;

x + 0 = x − существует единственный нулевой элемент 0 ( x + 0 = x для любого x из L);

x + (− x) = 0 − для каждого элемента x из L существует единственный противоположный элемент −x ( x + (−x) = 0 для любого x из L).

2. Каждой паре x и α, где α − число, а x элемент из L, отвечает элемент α·x, наываемый произведением α и x, причём:

α·(β·x) = (α·β)·x − умножнение на число ассоциативно: ;

1·x = x − для любого элемента x из L.

3. Операции сложения и умножения на число связаны соотношениями:

α·(x + y) = α·x + α·y − умножнение на число дистрибутивно относительно сложения элементов;

(α + β)·x = α·x + β·x − умножнение на вектор дистрибутивно относительно сложения чисел.

Набор векторов   называется системой векторов.

Система из   векторов   называется линейно зависимой, если существуют такие числа  , не все равные нулю одновременно, что

(1.1)

Система из   векторов   называется линейно независимой, если равенство (1.1) возможно только при  , т.е. когда линейная комбинация в левой части равенства (1.1) тривиальная.

Замечания 1.2

1. Один вектор   тоже образует систему: при   — линейно зависимую, а при   — линейно независимую.

2. Любая часть системы векторов называется подсистемой.

Свойства линейно зависимых и линейно независимых векторов

1. Если в систему векторов входит нулевой вектор, то она линейно зависима

.

2. Если в системе векторов имеется два равных вектора, то она линейно зависима.

3. Если в системе векторов имеется два пропорциональных вектора  , то она линейно зависима.

4. Система из   векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.

5. Любые векторы, входящие в линейно независимую систему, образуют линейно независимую подсистему.

6. Система векторов, содержащая линейно зависимую подсистему, линейно зависима.

7. Если система векторов   линейно независима, а после присоединения к ней вектора   оказывается линейно зависимой, то вектор   можно разложить по векторам  , и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.

Докажем, например, последнее свойство. Так как система векторов   — линейно зависима, то существуют числа  , не все равные 0, что . В этом равенстве  . В самом деле, если  , то  . Значит, нетривиальная линейная комбинация векторов   равна нулевому вектору, что противоречит линейной независимости системы  . Следовательно,   и тогда  , т.е. вектор   есть линейная комбинация векторов  . Осталось показать единственность такого представления. Предположим противное. Пусть имеется два разложения   и  , причем не все коэффициенты разложений соответственно равны между собой (например,  ).

Тогда из равенства   получаем  .

Следовательно, линейная комбинация векторов   равна нулевому вектору. Так как не все ее коэффициенты равны нулю (по крайней мере  ), то эта комбинация нетривиальная, что противоречит условию линейной независимости векторов  . Полученное противоречие подтверждает единственность разложения.

Векторное пространство   называется n-мерным, если в нем можно найти n линейно независимых векторов, но больше, чем n линейно независимых векторов оно не содержит.

Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов.

Пространство, имеющее конечную размерность, называется конечномерным. Пространство, в котором можно найти сколь угодно много линейно независимых векторов, называется бесконечномерным.

Совокупность n линейно независимых векторов n- мерного векторного пространства   называется его базисом.

Если каждой паре векторов x, y линейного пространства L поставлено в соответствие действительное число (x, y), так, что для любых x, y и z из L и любого действительного числа α справедливы следующие аксиомы:

(x, y) = (y, x),

(α·x, y) = α·(x, y),

(x + y, z) =(x, z) + (y, z),

(x, x)> 0 при x ≠ 0, (0, 0) = 0,

то в пространстве L определено скалярное произведение (x, y).

Если в линейном пространстве определено скалярное произведение, то такое пространство называется евклидовым пространством.

Теорема 1 (неравенство Коши-Буняковского)

Для любых чисел  .

Доказательство

При   неравенство   верно. Допустим, . Докажем, что . Перепишем это неравенство, частично раскрыв скобки: . Легко заметить, что для того, чтобы доказать это неравенство, достаточно доказать Перенеся все слагаемые в одну сторону, и сгруппировав их, получаем очевидное неравенство: А это и доказывает неравенство Коши-Буняковского.

Определение 2

1. Число   называется средним арифметическим чисел  . 2. Если  , то число   называется средним геометрическим чисел  .

Теорема 3 (неравенство Коши)

Пусть  , тогда .                           (1)

Доказательство

Шаг первый: сначала индукцией докажем это неравенство для натуральных чисел вида  . При m=1 надо доказать, что  . Это неравенство эквивалентно  , то есть  . Последнее неравенство верно, значит, и первоначальное верно, так как они равносильны. Допустим, неравенство верно при m=k, то есть .                              (2) Докажем неравенство (1) для m=k+1, то есть докажем, что . В самом деле,  . Итак, мы доказали неравенство Коши, когда количество чисел в средних есть степень двойки. А как быть с остальными? Для них мы докажем неравенство Коши, используя еще одну модификацию индукции – "индукцию вниз". Допустим, что неравенство Коши верно для n=k, то есть допустим, что ,                            (3) и докажем это неравенство для n=k-1. Для этого в неравенстве Коши положим  , тогда (3) будет иметь вид: После элементарных алгебраических преобразований получили: . Сократим неравенство на второй множитель правой части: . И, наконец, возведем обе части неравенства в степень  : . Неравенство Коши доказано полностью.

Билет 14

Прямая на плоскости

     Ответ :Общее уравнение 

Ax + By + C (  > 0).

     Вектор   = (А; В) - нормальный вектор прямой.

     В векторном виде:   + С = 0, где   - радиус-вектор произвольной точки на прямой (рис. 4.11).

     Частные случаи:

     1) By + C = 0 - прямая параллельна оси Ox;

     2) Ax + C = 0 - прямая параллельна оси Oy;

     3) Ax + By = 0 - прямая проходит через начало координат;

     4) y = 0 - ось Ox;

     5) x = 0 - ось Oy.

Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором этой прямой.

Направляющий вектор произвольной прямой в дальнейшем обозначается буквой  , его координаты - буквами l, m, n:

.

Если известна одна точка   прямой и направляющий вектор  , то прямая может быть определена (двумя) уравнениями вида

Каноническое уравнение прямой 

ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

П оложение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М₁ и вектора  , параллельного этой прямой.

Вектор  , параллельный прямой, называется направляющим вектором этой прямой.

Итак, пусть прямая l проходит через точку М₁(x₁, y₁, z₁), лежащую на прямой параллельно вектору  .

Рассмотрим произвольную точку М(x,y,z) на прямой. Из рисунка видно, что  .

Векторы   и   коллинеарны, поэтому найдётся такое число t, что  , где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М₁ и М соответственно через   и  , получаем  . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М, лежащей на прямой.

Запишем это уравнение в координатной форме. Заметим, что  ,   и   отсюда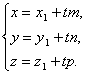 

Полученные уравнения называются параметрическими уравнениями прямой.

При изменении параметра t изменяются координаты x, y и z и точка М перемещается по прямой.