2. Если система (2.3) имеет единственное решение, определяемое по формулам: .

3. Если = =0, система имеет бесконечно много решений.

4. Если =0, а хотя бы один из система не имеет решений.

Билет 5

1) Минор n-ого порядка.

2) Ранг матрицы.

Ответ 1. Рангом матрицы   называется наибольший из порядков миноров матрицы   , отличных от нуля. Ранг нулевой матрицы считается равным нулю.         

Единое, стандартное, обозначение ранга матрицы отсутствует. Однако ув. Глухов показывал нам, что он обозначается как rang A (основной) и rang A (“A” с черточкой наверху – расширенный ранг), позже покажу.

2. Теперь то, что касается ранга матрицы.

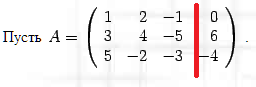
Теперь возвращаемся к рангам. Вспоминаем, что ранг – это НАИБОЛЬШИЙ из порядков МИНОРОВ. Всего таких порядков может быть дохуища, все зависит от того, насколько огромна матрица. В данной матрице порядков будет не более 3, но еще неизвестно, сколько из них будут не равны нулю.

Начинаем по порядку. Ищем миноры ПЕРВОГО порядка. Таковым является любое число в матрице.

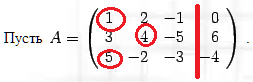
Таким образом 1,4,5 у меня миноры ПЕРВОГО порядка.

Ищем миноры ВТОРОГО порядка. Это будет пересечение строк и столбцов (т.е. то, что мы рассматривали выше). Найдем минор 3 строки 3 столбца.

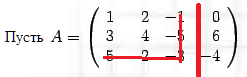
С читаем получаем -2 не равное 0.

Дальше рассматриваем минор третьего порядка. Это определитель который мы считали треугольниками.

Видим, что максимальный порядок, т.е. ТРЕТИЙ - НЕ РАВЕН (если бы 3ий порядок был равен нулю, было бы rang=2) нулю, следовательно ранг матрицы = 3 ( rang A = 3)

Думаю, с этим понятно. Ну это трудный способом, но эффективный, можно посчитать так. Запоминаем, что РАНГ матрицы соответствует НАИБОЛЬШЕМУ порядку не равному нулю. Т.е. если бы у нас определитель третьего порядка был бы =0, то у нас было бы rang A= 2

Есть еще одна фишка. Можно привести матрицу вида

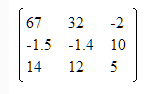
К треугольной, получим

Видно, что число НЕНУЛЕВЫХ строк, равно 3 => rang = 3 это основной ранг матрицы. Но есть и РАСШИРЕННЫЙ.

Например, если бы у нас была бы матрица:

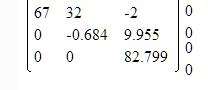
То расширенным рангом называлась бы область, которая включает все нули (т.е. 4 столбец), но тем не менее видим, что НУЛЕВЫХ строк нет, следовательно ОСНОВНОЙ ранг равен 3 и ранг РАСШИРЕННЫЙ равен 3

Ну понятно, что если 82.799 было бы равно нулю, то ранг был бы соответственно равен 2.

С рангами все, дальше.

3) Теорема Кронекера–Капелли (критерий совместности системы линейных уравнений). 

Ответ Для того чтобы система линейных уравнений была совместной, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу ее расширенной матрицы, т.е.  . В противном случае система не совместна.

Замечание. Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение, если же ранг меньше числа неизвестных, то система имеет множество решений. (об этом позже, это неопределенности)

Начнем с охуительного примера.

Пример 13. Исследовать систему линейных уравнений

Решение. Составим расширенную матрицу системы и с помощью элементарных преобразований вычислим одновременно ранги обеих матриц.

Далее умножим вторую строку на -2 и сложим с третьей, а затем сложим третью строку с последней. Имеем

.

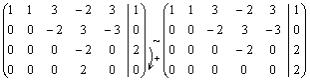Вспомнили как решается матрица методом гаусса? Идем дальше. Нас интересует это:

В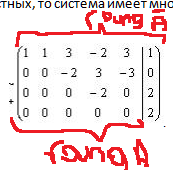 ыше я объяснял, что такое ранг ОСНОВНОЙ и ранг РАСШИРЕННЫЙ. Так вот, согласно теореме Кронекера-Капелли, данная хуйня будет несовместной, так как rang A (основной) = 3 (т.к. кол-во НЕНУЛЕВЫХ строк равно 3), а rang A (с черточкой над А, расширенный) = 4. Доказывается эта теорема на примере обычной матрицы, думаю ни у кого не составит труда накалякать матрицу и объяснить. Для танкистов, которые еще не поняли ОСНОВНОЙ и РАСШИРЕННЫЙ ранги:

4) Определенность-неопределенность

Ответ Исследовать систему линейных уравнений – означает определить, какой является эта система – совместной или несовместной, и в случае её совместности выяснить, определённая эта система или неопределённая.

Условие совместности системы линейных уравнений даёт следующая теорема

Теорема (Кронекера–Капелли).

Система линейных уравнений совместна  тогда и только тогда, когда ранг основной матрицы системы равен рангу её расширенной матрицы:

Для совместной системы линейных уравнений вопрос о её определённости или неопределённости решается с применением следующих теорем.

Теорема 1 Если ранг основной матрицы совместной системы равен числу неизвестных, то система является определённой

Теорема 2 Если ранг основной матрицы совместной системы меньше числа неизвестных, то система является неопределённой.

Таким образом, из сформулированных теорем вытекает способ исследования систем линейных алгебраических уравнений. Пусть n – количество неизвестных,     Тогда:

1) при   система несовместна;

2) при   система совместна, причём, если  , система определённая; если же  , система неопределённая.

Определение Базисным решением неопределённой системы линейных уравнений называют такое её решение, в котором все свободные неизвестные равны нулю.

Пример. Исследовать систему линейных уравнений

и в случае неопределённости системы найти её базисное решение.

Вычислим ранги основной   и расширенной матриц   данной системы уравнений, для чего приведём расширенную (а вместе с тем и основную) матрицу системы к ступенчатому виду:

Вторую строку матрицы сложим с её первой строкой, умноженной на   третью строку – с первой строкой, умноженной на   а четвёртую строку – с первой, умноженной на   получим матрицу

К третьей строке этой матрицы прибавим вторую строку, умноженную на   а к четвёртой строке – первую, умноженную на   Врезультате получим матрицу

удаляя из которой третью и четвёртую строки получим ступенчатую матрицу

Таким образом,     Следовательно, данная система линейных уравнений совместна, а поскольку величина ранга меньше числа неизвестных, система является неопределённой. Полученной в результате элементарных преобразований ступенчатой матрице соответствует система уравнений

Неизвестные   и   являются главными, а неизвестные   и   свободными. Придавая свободным неизвестным нулевые значения, получим базисное решение данной системы линейных уравнений:

Думаю с этим все понятно.