Вопрос37. Первый и второй замечательный пределы и следствия из них.

Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны:

Первый замечательный предел:

Второй замечательный предел:

Следствия

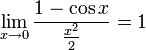
Следствия

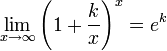
для ,

(а доказательство там-вообще долбанись)

Вопрос38. Сравнение бесконечно малых. Свойства эквивалентных бесконечно малых. И их таблица.

Сравнение бесконечно малых функций.

Пусть и — две функции, бесконечно малые в точке . Если , то говорят, что более высокого порядка малости, чем и обозначают . Если же , то более высокого порядка малости, чем ; обозначают . Бесконечно малые функции и называются бесконечно малыми одного порядка малости, если , обозначают .  И, наконец, если  не существует, то бесконечно малые функции и несравнимы.  

ПРИМЕР 2.  Сравнение бесконечно малых функций

Эквивалентные бесконечно малые функции.

Если , то бесконечно малые функции и называются эквивалентными, обозначают ~ .

Свойства эквивалентных бесконечно малых:

1. Разность двух эквивалентных бесконечно малых есть бесконечно малая высшего порядка относительно каждой из них.

2. Если из суммы нескольких бесконечно малых разных порядков отбросить бесконечно малые высших порядков, то оставшаяся часть, называемая главной, эквивалентна всей сумме.

Из первого свойства следует, что эквивалентные бесконечно малые могут сделаться приближенно равными со сколь угодно малой относительной погрешностью. Поэтому знак мы применяем как для обозначения эквивалентности бесконечно малых, так и для записи приближенного равенства их достаточно малых значений.

α(x)→0

1	sinα(x)~α(x)
2	arcsinα(x)~α(x)
3	tgα(x)~α(x)
4	arctgα(x)~α(x)
5	loga(1+α(x))~(logae)α(x)
6	ln(1+α(x))~α(x)
7	aα(x)-1~α(x)lna,a>0,a≠1
8	eα(x)-1~α(x)
9	(1+α(x))μ-1~μα(x)
10	1+α(x)n-1~α(x)n
11	1+α(x)-1~α(x)2
12	1-cosα(x)~12α2(x)

Вопрос39. Односторонние пределы в точке. Различные определения непрерывности функции в точке. Непрерывность суммы, произведения, частного двух функций. Непрерывность элементарной функции.

ОДНОСТОРОННИЕ ПРЕДЕЛЫ

Д о сих пор мы рассматривали определение предела функции, когда x→a произвольным образом, т.е. предел функции не зависел от того, как располагалось x по отношению к a, слева или справа от a. Однако, довольно часто можно встретить функции, которые не имеют предела при этом условии, но они имеют предел, если x→a, оставаясь с одной стороны от а, слева или справа (см. рис.). Поэтому вводят понятия односторонних пределов.

Если f(x) стремится к пределу b при x стремящемся к некоторому числу a так, что xпринимает только значения, меньшие a, то пишут и называют bпределом функции f(x) в точке a слева.

Таким образом, число b называется пределом функции y=f(x) при x→aслева, если каково бы ни было положительное число ε, найдется такое число δ (меньшее a), что для всех выполняется неравенство .

Аналогично, если x→a и принимает значения большие a, то пишут и называют b пределом функции в точке а справа. Т.е. число b называется пределом функции y=f(x) при x→a справа, если каково бы ни было положительное число ε, найдется такое число δ (большее а), что для всех выполняется неравенство .

Заметим, что если пределы слева и справа в точке a для функции f(x) не совпадают, то функция не имеет предела (двустороннего) в точке а.

Примеры.

Р ассмотрим функцию y=f(x), определенную на отрезке [0,1] следующим образом

Найдем пределы функции f(x) при x→3. Очевидно, , а .

.

.

Непрерывность функции в точке. 

  Определение. Функция f(x), определенная в окрестности некоторой точки х₀, называется непрерывной в точке х₀, если предел функции и ее значение в этой точке равны, т.е.

 

Тот же факт можно записать иначе:

 

  Определение. Если функция f(x) определена в некоторой окрестности точки х₀, но не является непрерывной в самой точке х₀, то она называется разрывной функцией, а точка х₀ – точкой разрыва.

Функциональные ряды Примеры решения задач математика

Пример непрерывной функции:

 y

 

 f(x₀)+

 f(x₀)

 f(x₀)-

 

0 x₀- x₀ x₀+  x 

Пример разрывной функции:

 

  y

 

 f(x₀)+

 f(x₀)

 f(x₀)-

  x₀ x

 

  Определение. Функция f(x) называется непрерывной в точке х₀, если для любого положительного числа >0 существует такое число >0, что для любых х, удовлетворяющих условию

верно неравенство  .

 

  Определение. Функция f(x) называется непрерывной в точке х = х₀, если приращение функции в точке х₀ является бесконечно малой величиной.

 

f(x) = f(x₀) + (x)

где (х) – бесконечно малая при хх₀.

 Свойства непрерывных функций.

1) Сумма, разность и произведение непрерывных в точке х₀ функций – есть функция, непрерывная в точке х₀.

 

2) Частное двух непрерывных функций – есть непрерывная функция при условии, что g(x) не равна нулю в точке х₀.

  Гексаэдр - правильный шестигранник Вычислим интеграл Математика Задачи Ортогональная система координат в пространстве Математическая модель

  3) Суперпозиция непрерывных функций – есть непрерывная функция.

Это свойство может быть записано следующим образом:

Если u = f(x), v = g(x) – непрерывные функции в точке х = х₀, то функция v = g(f(x)) – тоже непрерывнаяфункция в этой точке.

 

  Справедливость приведенных выше свойств можно легко доказать, используя теоремы о пределах.

Непрерывность некоторых элементарных функций.

  1) Функция f(x) = C, C = const – непрерывная функция на всей области определения.

  2) Рациональная функция  непрерывна для всех значений х, кроме тех, при которых знаменатель обращается в ноль. Таким образом, функция этого вида непрерывна на всей области определения.

 

  3) Тригонометрические функции непрерывны на своей области определения.

Докажем свойство 3 для функции y = sinx.

Запишем приращение функции y = sin(x + x) – sinx, или после преобразования:

Действительно, имеется предел произведения двух функций  и . При этом функция косинус – ограниченная функция при х0 , а т.к.

предел функции синус , то она является бесконечно малой при х0.

Таким образом, имеется произведение ограниченной функции на бесконечно малую, следовательно это произведение, т.е. функция у – бесконечно малая. В соответствии с рассмотренными выше определениями, функция у = sinx – непрерывная функция для любого значения х = х₀ из области определения, т.к. ее приращение в этой точке – бесконечно малая величина.

Аналогично можно доказать непрерывность остальных тригонометрических функций на всей области определения.

Вообще следует заметить, что все основные элементарные функции непрерывны на всей своей области определения.