6. Комплексный метод расчёта электрических цепей синусоидального тока. Неразветвлённая цепь.

Если сопротивление R, индуктивность L и емкость Свключены последовательно под напряжение U и ток определяется уравнением i=I_msint, то уравнение напряжений имеет вид:

.

В комплексной форме это уравнение можно записать

,

или, разделив на и перейдя к комплексам, ,

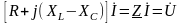где X_L–X_С – реактивное сопротивление цепи; Z=Ze^j=R+jX – комплексное сопротивление цепи; – полное сопротивление цепи.

На комплексной плоскости сумма напряжений будет представлена в виде диаграммы

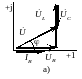
Если индуктивное сопротивление больше емкостного, т.е. X_L>X_C, то ток отстает от напряжения сети на угол φ (а) и наоборот при X_L<X_C ток опережает напряжение на угол φ (б). В первом случае цепь носит индуктивный характер, во втором – емкостной характер. Комплексное сопротивление тоже может быть представлено на комплексной плоскости в виде треугольника сопротивлений Z=R+jX.

При этом .

Мгновенная мощность в последовательной цепи

содержит постоянную составляющую и переменную составляющую, которая изменяется с двойной частотой сети. Постоянную составляющую, или среднее значение мгновенной мощности за период называют активной мощностью. Она измеряется в Ваттах (Вт).

Для оценки величины энергии, которая запасается в магнитном и электрическом полях и затем возвращается в сеть дважды за период, вводят понятие реактивной мощности Q=UIsinφ, которая измеряется в вольт-амперах реактивных (ВАр).

P=UIcosφ=U_RI=I²R.

Q=UIsin=I²X=I²X_L–I²X_C=Q_L–Q_C.

Произведение действующих значений напряжения и тока определяет полную мощность S=UI (ВА), которая измеряется в вольт-амперах. Отношение активной мощности к полной называют коэффициентом мощности .

Комплексный метод расчёта электрических цепей синусоидального тока. Разветвлённая цепь.

При параллельном включении напряжение на всех R, L, C элементах одинаково, а токи различны по величине и имеют различные фазовые сдвиги по отношению к напряжению – ток через сопротивление совпадает по фазе с напряжением, ток через индуктивность отстает на 90, а через емкость – опережает напряжение на 90. В комплексной форме токи можно записать следующим образом:

,

Суммарный ток равен ,

где b=b_L– b_C – реактивная проводимость; Y =g - jb – комплексная проводимость; – полная проводимость цепи. Активная, реактивная и полная проводимости образуют треугольник проводимостей. При этом .

Векторная диаграмма токов имеет следующий вид. Сначала проводим вектор тока через сопротивление (параллельно напряжению), затем из конца – вектор тока перпендикулярно напряжению (отстает от него на угол 90), затем – вектор перпендикулярно напряжению, но в противоположную сторону (вектор тока опережает напряжение на угол 90). Их сумма дает вектор суммарного тока . Фазовый сдвиг φ между суммарным током и напряжением может быть положительным (б) или отрицательным (в) в зависимости от соотношения параметров цепи L и C. В первом случае цепь носит активно-емкостный характер, во втором – активно-индуктивный (ток отстает от напряжения на угол φ). В общем случае, если известно комплексное сопротивление ветви, то комплексная проводимость этой ветви определяется следующим образом:

.