1.Визначники другого, третього, n–го порядків, їх властивості.
Определителем квадратной матрицы А называется число, которое вычисляется по некоторому заданному правилу и обозначается:
Так,
например, определитель 1-го порядка:
Для вычисления определителей более высокого порядка вводятся понятия минора и алгебраического дополнения элемента определителя.
Пусть
– определитель
2–го порядка.
Минором
элемента
определителя
называется
определитель,
полученный
вычёркиванием из матрицы А
i-той
строки
та j-того
столбца.
Алгебраическим
дополнением
элемента
називается
его
минор,
взятый
со
знаком
„+” или
„–”:
.
Визначником другого порядку називається вираз ∆, який обчислюється за правилом:
Визначник другого порядку дорівнює добутку елементів, що стоять на головній діагоналі, мінус добуток елементів, розміщених на другій діагоналі.
Теорема Лапласа:
Определитель матрицы равен сумме произведений элементов произвольной строки (или столбца) на их алгебраические дополнения.
(Раскладываем
по 1-й строке)
=
.
Нехай
- визначник 3–го порядку.
За теоремою Лапласа запишемо розклад визначника, наприклад, за елементами 1–го сповпця:
Свойства определителей:
1.При транспонировании определитель не меняется.
Док-во
2.Если в определителе поменять местами любые две параллельных строки, то определитель поменяет знак на противоположный, не изменяя абсолютной величины.
Доведення:
3.Если
определитель имеет две одинаковых
строки, то он равен нулю.
4.Для
того, чтобы умножить определитель на
число, нужно умножить на это число любую
одну его строку.
2. Означення оберненої матриці. Довести теорему (необхідну і достатню умову існування оберненої матриці).
Пусть А – квадратная матрица порядка n.
Матрица
порядка n называется обратной к матрице
А, если имеет место соотношение
Замечание: Обратные матрицы определены только для квадратных матриц, но не для каждой квадратной матрицы существует обратная.
Теорема: Для существования у матрицы А обратной матрицы необходимо и достаточно, чтоб матрица А была невырожденной.
Доказательство:
Необходимость:
По
определению обратной матрицы, имеете
место равенство
,
тогда
!
!
= !
*А!
=!Е! или !
!
= 1
По свойству определителей, определитель от произведения матриц равен произведению их определителей, поэтому
Достаточность:
Поскольку то существует матрица
3. Системи n лінійних рівнянь з n невідомими, основні означення. Правило Крамера.
Системой n-линейных ур-ний с n неизвестными называется система вида
В которой а и в - произвольные числа, которые называются коэффициентами при неизвестных и свободными членами соответственно.
Решением системы называется упорядоченный набор из m чисел, при подстановки которых в систему вместо неизвестных получаем n-тождеств.
Система линейных уравнений (СЛУ) может иметь одно решение, либо не одного, либо бесконечно много решений.
Система называется совместной, если она имеет хотя бы одно решение; в противном случае она называется несовместной. Совместная система называется определённой, если у неё только одно решение.
Систему линейных ур-ний можно записать в матричном виде A*X = B
- матрица
коэффициентов
-
столбец xнеизвестных;
-
столбец свободных членов
Теорема:
Пусть
n=m и матрица А невырожденная
,
тогда у системы существует единственное
решение, определяемое формулой
Теорема (правило Крамера):
Пусть n=m и матрица А невырожденная, тогда у системы существует единственное решение, элементы которого находятся по формулам
;
;
…;
,
где
- определители матриц, получаемых из
матрицы А заменой j-го
столбца столбцом свободных членов.
Доведення:
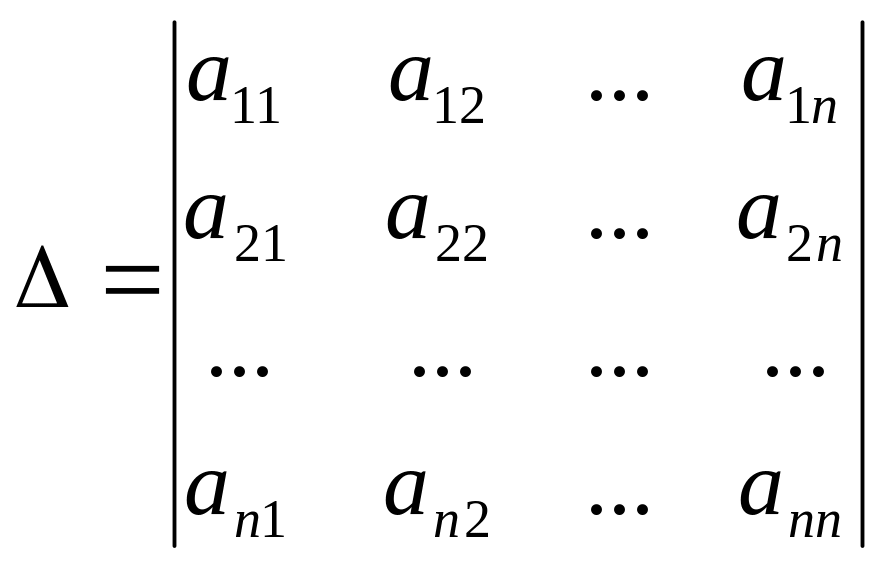
Знайдемо алгебраїчні доповнення Аij (i=1,n;j=1,n)
Для визначення невідомого x1, помножимо перше рівняння системи на А11, друге – на А21, n-не – на Аn1 і отримані рівності додамо:
Коефіцієнт при х1 дорівнює визначнику ∆, права частина = ∆1, коефіцієнти при xk (k=2,3,…,n)=0/
Таким чином x1*∆=∆1,
Якщо продовжити описаний процес, то отримаємо:
xj*∆ =∆j
Приклад. Розв’язати систему рівнянь за правилом Крамера.
.