Прогрессии Арифметическая прогрессия

Числовую последовательность {a_n}, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом d, называютарифметической прогрессией. Число d называется разностью арифметической прогрессии: 

an + 1 = an + d.

Так как a_n – 1 = a_n – d, то a_n + 1 + a_n – 1 = 2a_n. Верно и обратное.

Последовательность   является арифметической тогда и только тогда, когда для любого n > 1 выполняется рекуррентное соотношение 

Формула общего члена арифметической прогрессии {a_n} такова: 

an = a1 + (n – 1) · d.

Доказательство

Докажем это пользуясь методом математической индукции. Легко убедиться, что для n = 1 данная формула верна. Пусть эта формула верна для n = k. Докажем ее справедливость для n = k + 1. Имеем ak + 1 = ak + d = a1 + (k – 1) · d + d = a1 + k · d. Теорема доказана.

Сумма n первых членов арифметической прогрессии {a_n} равна 

Обе формулы легко доказать, используя метод математической индукции. Выполните это самостоятельно.

  

2)   Арифметическая прогрессия  Арифметическая прогрессия - числовая последовательность   определяемая условиями: 1)   2)  (d - разность арифметической прогрессии).

 Свойства арифметической прогрессии:

     Формула n-го члена: 

     Формулы суммы n первых членов:

     Геометрическая прогрессия    Геометрическая прогрессия - числовая последовательность   определяемая условиями: 1)   2)   n = 1, 2, ... (q - знаменатель геометрической прогрессии).

   Свойства геометрической прогрессии:

     Формула n-го члена: 

     Формулы суммы n первых членов  :

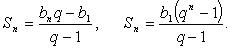
     Сумма бесконечной геометрической прогрессии:

Геометрическая прогрессия(убывающая)

Числовую последовательность {b_n}, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же число q ≠ 0, называют геометрической прогрессией:

bn + 1 = bn · q.

Важно отметить, что число q, которое называется знаменателем прогрессии, отлично от нуля. Так как 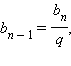   то   Верна и обратная теорема.

Последовательность {b_n} является геометрической тогда и только тогда, когда для любого n > 1 выполняется соотношение 

где   при всех n. Тем не менее, важно понимать, что формула   справедлива только для геометрической прогрессии с положительными членами, а предыдущее соотношение верно для произвольной геометрической прогрессии.

Каждый член геометрической прогрессии {b_n} определяется формулой 

bn = b1 · qn – 1.

Доказательство

Докажем это пользуясь методом математической индукции. Легко убедиться, что при n = 1 данная формула верна. Пусть эта формула верна для n = k. Докажем ее справедливость для n = k + 1. Имеем bk + 1 = bk · q = b1 · qk – 1 · q = b1 · qk. Теорема доказана.

Сумма n первых членов геометрической прогрессии {b_n} равна 

при q ≠ 1 и S_n = n · b₁ при q = 1.

Эти формулы также доказываются методом математической индукции. Докажите их самостоятельно.

При |q| < 1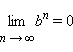 , поэтому в этом случае геометрическая прогрессия называется бесконечно убывающей. Суммой бесконечно убывающей геометрической прогрессии называется число 

,

где S_n – сумма n первых членов геометрической прогрессии.

Сумма бесконечно убывающей геометрической прогрессии (|q| < 1) равна 

Для доказательства достаточно заметить, что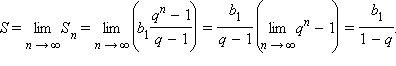   

20. Исследование функций на экстремумы.

Слово «экстремум» значит крайний. Точкой экстремума называется такая точка, в которой функция принимает крайние значения: наибольшее или наименьшее.

Критической точкой функции называется такая точка ее области определения, в которой производная функции обращается в нуль или не существует. Критические точки функции, в которых она меняет возрастание на убывание или убывание на возрастание, называются точками экстремума.

Если в точке экстремума функция меняет убывание на возрастание, то в этой точке достигается наименьшее значение хотя бы на небольшом участке ее области определения. Говорят, что такая точка является точкой локального минимума.

Если в точке экстремума функция меняет возрастание на убывание, то в этой точке достигается наибольшее значение хотя бы на небольшом участке ее области определения. Говорят, что такая точка является точкой локального максимума.

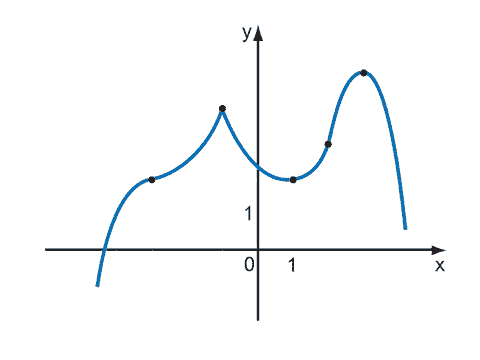
Задача исследования функции на экстремумы состоит из следующих шагов:

1. находят производную данной функции;

2. находят критические точки;

3. устанавливают, какие из критических точек являются точками экстремума, одновременно уточняя характер локального экстремума: максимум или минимум;

4. устанавливают, чему равны сами эти локальные максимумы и минимумы.

 

20. Графики обратных тригонометрических функций.

а Обратные тригонометрические функции Обратные тригонометрические функции это математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:

• арксинус (обозначение: arcsin)

• арккосинус (обозначение: arccos)

• арктангенс (обозначение: arctg)

• арккотангенс (обозначение: arcctg)

• арксеканс (обозначение: arcsec)

• арккосеканс (обозначение: arccosec)

Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arc — дуга).  Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. 

Функция y = arcsin x Дана функция y = sin x.  На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arcsin x функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений —  −2 ;2  . Так как для функции y = sin x на интервале  −2 ;2   каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция y = arcsin x, график которой симметричен графику функции y = sin x на отрезке  −2 ;2   относительно прямой y = x.
Функция y = arccos x Дана функция y = cos x.  На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arccos x функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения — [0; ]. На этом отрезке y = cos x строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке [0; ] существует обратная функция y = arccosx, график которой симметричен графику y = cos xна отрезке [0; ] относительно прямойy = x.
Функция y = arctg x Дана функция y = tg x.  На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arctgx функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз —  −2 ;2  . На этом отрезке y = tg x строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале  −2 ;2  существует обратная функция y = arctg x, график которой симметричен графику y = tgx на отрезке  −2 ;2  относительно прямой y = x.