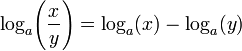- •2)Свойства:
- •2)Свойства логарифмов
- •2)Аксиомы стереометрии и их следствия
- •3)Взаимное расположение прямых в пространстве.
- •4)Взаимное положение прямых и плоскостей в пространстве.
- •Декартова система координат
- •1)Уравнение окружности
- •Системы координат в пространстве: декартовы
- •9.1. Векторы в пространстве
- •Скалярное произведение векторов
- •Расстояние между точками
- •Радианная мера угла
- •Прогрессии Арифметическая прогрессия
- •Геометрическая прогрессия(убывающая)
ОТВЕТЫ НА ЭКЗАМЕН ПО МАТЕМАТИКЕ
Целые и рациональные числа. Действительные числа. Стандартная запись числа. Действия с числами в стандартном виде.
1)Целые
числа –
это множество Z
чисел
{0, 1, -1, 2, -2, ....}, состоящих из натуральных
чисел, отрицательных чисел (противоположные
натуральным числам) и число 0 (нуль)
составляют.
Целые числа могут быть записаны в виде
дробей 4 ;
-5=
;
-5= .
2)Рациональные
числа –
это множество Q
чисел,
состоящее из положительных и отрицательных
целых и дробных чисел и число 0. Любое
рационаьное число можно представить в
виде дроби
.
2)Рациональные
числа –
это множество Q
чисел,
состоящее из положительных и отрицательных
целых и дробных чисел и число 0. Любое
рационаьное число можно представить в
виде дроби![]() ,
где m — целое число, а n — натуральное
число. Значит, N
содержится в Z,
а Z
в Q.
NZQ.
Также в качестве примеров
рациональных чисел можно привести:
,
где m — целое число, а n — натуральное
число. Значит, N
содержится в Z,
а Z
в Q.
NZQ.
Также в качестве примеров
рациональных чисел можно привести: ![]() ,
,![]() ,
,![]() .
3)Действительные
(вещественные) числа –
Множество Q
всех
рациональных чисел и множество I
всех
иррациональных чисел называется
множество R
действительных или вещественных чисел,
т.е. QR,
IR.
Действительным
числом называется конечная или бесконечная
десятичная дробь.
Приближенное
значение. Абсолютная и относительная
погрешности.
.
3)Действительные
(вещественные) числа –
Множество Q
всех
рациональных чисел и множество I
всех
иррациональных чисел называется
множество R
действительных или вещественных чисел,
т.е. QR,
IR.
Действительным
числом называется конечная или бесконечная
десятичная дробь.
Приближенное
значение. Абсолютная и относительная
погрешности.
1)Приближенное значение – это округление значения какой либо измерительной единицы до целых. Число (=|x-a|) называют приближенным значением х с точностью до a, если абсолютная погрешность приближенного значения а не привышает а. Правило округления: Если первая отбрасываемая цифра меньше 5 то нужно брать приближение по недстатку если первая отбрасываемая цифра больше или равна 5 то нужно брать по избытку. При округлении числа до какого-нибудь разряда, цифры во всех следующих разрядах заменяют нулями, а стоящие после запятой, отбрасывают. Пример. Допустим число 154.376 = 154.4 2)Погрешностью приближения (абсолютной погрешностью) называют модуль(абсолютная веичина) разности между точным значением величины х и ее приближенным значением а: погрешность приближения — это | х - а |= , - абсолютная погрешность. Например, погрешность приближенного равенства 3,141 или 3,142 выражается как, |-3,141|или соответственно как |-3,142|.Число а (а|x-a|) называется границей абсолютной погрешности приближенного числа а.
3)Относительная
погрешность —
погрешность измерения, выраженная
отношением абсолютной погрешности
измерения
этого приближения к действительному
или измеренному значению измеряемой
величины(или к числу а) = .
Абсолютная
погрешность бывает неизвестна тогда
мы используем некое число
(называется границей относительнйо
погрешности) которое меньше этого модюля
||
.
а
=
.
Абсолютная
погрешность бывает неизвестна тогда
мы используем некое число
(называется границей относительнйо
погрешности) которое меньше этого модюля
||
.
а
=
 .
.
Понятие комплексного числа. Действия над комплексными числами. Изображение комплексных чисел.
1)Комплексным числом называется числа вида z = a+bi, где a и b – любые действительные числа, i – специальное число, определяется равнеством i2 = -1 которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом:
Два
комплексных числа a1 + ib1 и а2 + ib2 называются
равными тогда и только тогда, когда а1=а2
и
в1=в2
2)Заметим,
что арифметические операции над
комплексными числами вида z = a +
0i
осуществляются точно так же, как и над
действительными числами. Действительно, ![]()
![]()
|
|
|
1)Степень с натуральным показателем.Степенью числа a с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен a:
an = В выражении an : - число а (повторяющийся множитель) называют основанием степени - число n (показывающее сколько раз повторяется множитель) – показателем степени Например,4 . 4 . 4 . 4 . 4 . 4=46 Отметим, что основание степени может быть любым числом. Степень с натуральным показателем. Произведение нескольких одинаковых множителей можно записать в виде выражения, называемого степенью. Определение. Степенью числа а с натуральным показателем п, большим 1, называется произведение п множителей, каждый из которых равен а. Определение. Степень числа а, не равного нулю, с нулевым показателем равна единице. Степенью числа а с показателем 1 называется само число. Нахождение значения степени называют возведением в степень. Примеры: 75 = 7 . 7 . 7 . 7 . 7. = 16 807, (– 8)3 = (– 8) . (– 8) . (8) = – 512 . 2)Свойства степени с натуральным показателем: 1.умножении степеней am · an = am + n например: 71.7 · 7 - 0.9 = 71.7+( - 0.9) = 71.7 - 0.9 = 70.8 2. делении степеней am / an = am — n ,где, m > n, например: 133.8 / 13 -0.2 = 13(3.8 -0.2) = 133.6 3. возведении степени в степень (am )n = a m · n например: (23)2 = 2 3·2 = 26 4.возведении в степень произведения (a · b)n = an · b m , например:(2·3)3 = 2n · 3 m , 5. При возведении в степень дроби (a / b)n = an / bn например: (2 / 5)3 = (2 / 5) · (2 / 5) · (2 / 5) = 23 / 53 6.
Возведение рациональной дроби в отрицательную степень происходит по следующей формуле: (P/Q)−n=(P/Q)n
|
|
Корень n-ой степени. Свойства корней.
1)Корень n-ой степени. Корнем n-ой степени из числа a называется такое число, n-я
степень которого равна a (nN).
Арифметический
корень n-й степени (n >
0) из числа a —
это такое число b,
что bn = a.
В поле действительных
чисел корень
может иметь до двух решений или ни
одного, если это корень чётной степени
из отрицательного числа. В поле комплексных
чисел корень n-й
степени имеет n решений.
Обозначается символом ![]() .
.
Арифметический
корень 2-й степени называется квадратным
корнем[1] и
может записываться без указания
степени: ![]() .
Арифметический корень 3-ей степени
называетсякубическим
корнем[2].
.
Арифметический корень 3-ей степени
называетсякубическим
корнем[2].
2)Свойства:
![]()
![]()
![]()
![]()
![]()
![]()
![]() НАПИСАТЬ
ПРИМЕРЫ!!!
НАПИСАТЬ
ПРИМЕРЫ!!!
Степень с рациональным и действительным показателем.
Степень
числа с рациональным показателем.Степенью
числа а > 0 с рациональным
показателем ![]() ,
где m – целое число, а n – натуральное
(n > 1), называется число
,
где m – целое число, а n – натуральное
(n > 1), называется число ![]()
Итак, ![]()
Например, ![]()
Степень числа 0 определена только для положительных показателей;
по определению 0r = 0 , для любого r > 0
Замечания
Из определения степени с рациональным показателем следует, что для любого положительного а и любого рационального r число ar положительно.
Любое рациональное число допускает различные записи его в виде дроби, поскольку
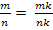 для
любого натурального k. Значение аr также
не зависит от формы записи рационального
числа r.
для
любого натурального k. Значение аr также
не зависит от формы записи рационального
числа r.При а < 0 рациональная степень числа а не определяется.
Для степеней с рациональным показателем сохраняются основные свойства степеней, верные для любых показателей (при условии, что основание степени будет положительным).
Логарифмы и их свойства. Десятичные и натуральные логарифмы.
1)Логарифм положительного
числа ![]() по
основанию
по
основанию ![]() (обозначается
(обозначается ![]() )
— это показатель степени,
в которую надо возвести
,
чтобы получить
. b
> 0, a
> 0, а≠
1.
)
— это показатель степени,
в которую надо возвести
,
чтобы получить
. b
> 0, a
> 0, а≠
1.
![]() ,
,![]()
Пример:
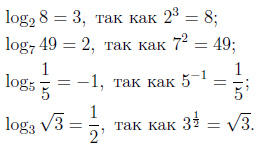
Десятичный
логарифм —
логарифм с основанием 10, который
обозначается как ![]() .
.
![]() ,
, ![]() ,
так как
,
так как ![]()
Натуральный
логарифм —
логарифм с основанием ![]() ,
обозначается
,
обозначается ![]()
2)Свойства логарифмов
1.
2.
3. 4.
5.
6.
7.
|
8.
9.
11.
12.
13.
|
Правила логарифмирования.
Логарифмирование – это нахождение логарифмов заданных чисел или выражений
Произведение |
|
|
Частное от деления |
|
|
Степень |
|
|
Корень |
|
|
9. Аксиомы стереометрии. Взаимное расположение прямых в пространстве. Взаимное расположение прямых и плоскостей в пространстве.
1)Стереометрия (объемная простраственая) — это раздел геометрии, в котором изучаются свойства фигур в пространстве.
Простейшие фигуры в пространстве: точка, прямая, плоскость.
2)Аксиомы стереометрии и их следствия
Аксиома1.
Через
любые три точки, не лежащие на одной
прямой, проходит плоскость, и притом
только одна.
![]()
Асиома2.
Если
две точки прямой лежат в плоскости, то
все точки прямой лежат в этой плоскости.
(Прямая лежит на плоскости или плоскость
проходит через прямую).
![]()
Из
аксиомы 2 следует, что если прямая не
лежит в данной плоскости, то она имеет
с ней не более одной общей точки. Если
прямая и плоскость имеют одну общую
точку, то говорят, что они пересекаются.

Аксиома3. Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
В
таком случае говорят, плоскости
пересекаются по прямой.Пример: пересечение
двух смежных стен, стены и потолка
комнаты.


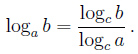 ,
частности, если c = b, то
,
частности, если c = b, то