15. Теорема об изменении кинетического момента механической системы в её относительном движении по отношению к центру масс

Ранее было доказано, что при любом произвольном движении механической системы:

Продифференцируем приведенное выражение:

с другой стороны:

Приравниваем правые части полученных выражений:

Производная по времени от вектора кинетического момента системы относительно центра масс в её относительном движении по отношению к этому центру равна главному моменту внешних сил действующих на систему относительно центра масс.

Из теоремы следует, что при сложном движении, движение механической системы относительно центра масс происходит так же, как если бы последний был неподвижен.

Примерами действия закона сохранения кинетического момента по отношению к подвижному центру масс, являются:

- изменение скорости вращения спортсмена при прыжках в воду когда он группируется вокруг центра масс;

- поворот туловища космонавта при вращении руками;

- стабилизация вращения и поворот находящегося на орбите космического аппарата с помощью вращающегося маховичка;

- поворот кошки лапами вниз во время падения;

- способность собаки, действуя хвостом, быстро поворачиваться огибая, деревья.

16. Дифференциальные уравнения поступательного движения. Дифференциальные уравнения во вращательном движении. Дифференциальные уравнения плоского (плоскопараллельного) движения твердого тела.

Дифференциальные уравнения поступательного движения.

Так как поступательное движение тела сводится к движению любой его точки, поэтому дифференциальными уравнениями поступательного движения будут являться проекции теоремы о движении центра масс на оси координат, где произвольной точкой будет центр масс.

Дифференциальные уравнения во вращательном движении.

Теорема об изменении кинетического момента системы:

Произведение углового ускорения тела на осевой момент инерции равно сумме моментов внешних сил относительно оси вращения.

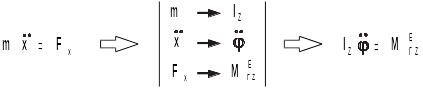
Аналогия между дифференциальными уравнениями движения поступательным и вращательным движением твердого тела:

Физический маятник и его колебания.

Физическим маятником называется тело, совершающее колебательное движение вокруг оси не проходящей через центр масс.

В случае малых колебаний .

Решение дифференциального уравнения:

Дифференциальные уравнения плоского (плоскопараллельного) движения твердого тела.

Кинематическими уравнениями плоского движения являются:

При плоском движении тело поступательно движется с некоторым полюсом О одновременно поворачиваясь вокруг этого полюса. Примем за полюс центр масс С, тогда с учетом теоремы о движении центра масс и дифференциальных уравнений вращательного движения, дифференциальные уравнения плоского движения запишутся в виде:

I_Zc – осевой момент инерции относительно оси, перпендикулярной плоскости движения, проходящей через центр масс.

Пример . Катушка массой m, с радиусами r и R находится под действием двух горизонтальных сил P₁ и P₂. Определить ускорение центра масс катушки при качении ее без скольжения..

Дифференциальные уравнения плоского движения:



О дно из условий качения без скольжения:

Так как колесо катится без скольжения применить закон Гука F=fN нельзя. Поэтому силу сцепления находим из уравнения (3):

(4)

Уравнение (4) подставляем в уравнение (1):