4.1.2. Теорема об изменении количества движения

Преобразуем основное уравнение динамики материальной точки следующим образом:

;

;

;

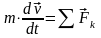. (4.1)

Производная по времени от количества движения материальной точки равна равнодействующей сил, действующих на точку.

Данное утверждение - это теорема об изменении количества движения материальной точки в дифференциальной форме.

В проекциях на декартовы оси координат имеем:

;

;

.

Преобразуем выражение (4.1) приняв, что :

;

;

.

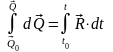Изменение количества движения материальной точки за некоторый промежуток t-t₀ времени равно импульсу равнодействующей сил, действующих на точку за тот же промежуток времени – рассматриваемая теорема в интегральной форме.

В проекциях на декартовы оси координат имеем:

;

;

.

Преобразуем уравнение (теорема о движении цента масс механической системы)

следующим образом:

;

;

.

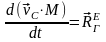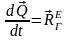Полученное уравнение выражает теорему об изменении количества движения механической системы в дифференциальной форме: производная от количества движения механической системы по времени равна главному вектору внешних сил, действующих на систему.

В проекциях на декартовы оси координат:

;

;

.

Рассматривается также теорема об изменении количества движения механической системы в интегральной форме: изменение количества движения механической системы равно импульсу главного вектора внешних сил, действующих на систему.

Т.е.

.

Или в проекциях на декартовы оси координат:

;

;

.

4.1.3. Следствия из теоремы

Если , то .

Если и/или и/или , то и/или и/или соответственно.

Аналогично и для материальной точки.

11.Уравнение Мещерского(основное уравнение динамики тела переменной массы)

Пусть тело массой m+dmдвижется со скоростью . Затем происходит отрыв от тела некоторой частицы массой dm движущейся со скоростью .

Количество движения системы после отрыва частицы:

Тогда изменение количества движения:

Исходя из теоремы об изменении количества движения системы:

Обозначим величину - относительная скорость частицы:

Обозначим

Получим -

Данная формула выражает основное уравнение динамики тела переменной массы (формула Мещерского).

Основное уравнение динамики тела переменной массы свидетельствует о том, что ускорение этого тела формируется не только за счет внешних сил, но и за счет реактивной силы.

Реактивная сила – это сила, родственная той, которую ощущает стреляющий человек - при стрельбе из пистолета она ощущается кистью руки; при стрельбе из винтовки воспринимается плечом.

Первая формула Циолковского (для одноступенчатой ракеты)

Для многих современных реактивных двигателей , где - максимально допускаемая конструкцией двигателя реактивная сила (тяга двигателя); - сила тяжести, действующая на двигатель, находящийся на земной поверхности. Изложенное позволяет составляющей в уравнении Мещерского пренебречь и к дальнейшему анализу принять это уравнение в форме: ,

Обозначаем:

- запас топлива (при жидкостных реактивных двигателях - сухая масса ракеты (остающаяся её масса после выгорания всего топлива);

- масса отделившихся от ракеты частиц; рассматривается как переменная величина, изменяющаяся от до .

.

Так как

Следовательно

,

где - характеристическая скорость – это скорость, которую приобретает ракета под действием тяги после извержения из ракеты всех частиц (при жидкостных реактивных двигателях – после выгорания всего топлива).

Вынесенная за знак интеграла (что можно делать на основании известной из высшей математики теоремы о среднем) - это средняя скорость извергаемых из ракеты частиц. Но, как видим, с точки зрения получения наибольшего значения характеристической скорости, должна быть как можно большей величиной. Поэтому на практике - это максимально достижимая скорость извержения частиц из ракеты. К сведению: в наиболее распространённых жидкостных реактивных двигателях (окислитель - жидкий кислород, азотная кислота, перекись водорода и др.; горючее - керосин, спирт, жидкий водород и т.д.) может достигать значений 3-3,5 км/с иногда до 4,5 км/с.Итак,

Вышеприведенное математическое выражение называют первой формулой Циолковского (или: формулой Циолковского для одноступенчатой ракеты), где - число Циолковского.

Реально достижимая характеристическая скорость - км/с. Чтобы ракета не смогла возвратиться на Землю (стала бы как и Луна спутником Земли, со средним расстоянием от земной поверхности в 200 км), необходимо достигать скоростей не менее 7,9 км/с, т.е. характеристическая скорость должна быть не меньшей км/с.

Следовательно, одноступенчатая ракета не способна, по сегодняшнему уровню научно-технических достижений, преодолеть земное притяжение – неотвратимо будет возвращаться на земную поверхность. Но выход из положения есть- это многоступенчатые ракеты.