24.Уравнений лагранжа 2-го рода

Рассматриваем инерциальную систему отсчёта, принимаем к рассмотрению механическую систему с удерживающими и голономными связями, в которой наряду со стационарными могут быть и нестационарные связи.. Принятую к рассмотрению механическую систему представляем состоящей из частиц. Их положение относительно инерциальной системы определяем радиус-векторами ; - степень её подвижности; - обобщённые координаты; - обобщённые скорости.

, где - возможная скорость -той точки, выраженная в долях скорости одиночной вариации -той обобщённой координаты (или – передаточное отношение от -той обобщённой координаты к -тому объекту механической системы – частице, телу).

И так, формулы для вычисления обобщённых сил:

, где

- вектор передаточного отношения от -той обобщённой координаты к -той точке.

Т.к. результат не зависит от скорости вариации обобщённой координаты, то при конкретных расчётах скорости вариаций обобщёнными координатами ( ) можно принимать равными единице (делить на единицу всегда проще), например 1 м/с.

При выводе уравнений Лагранжа 2-го рода будем пользоваться следующими математическими зависимостями.

Учитывая выше приведенные математические зависимости получим

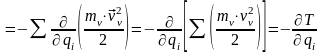
Окончательно получим

Преимущества уравнений Лагранжа:

нет сложностей с выбором принимаемой к рассмотрению механической системы и сложностей с учётом реакций связей;

облегчен поиск необходимой для решения задачи системы уравнений;

одинаковость вычислительные процедур у всех конкретных задач, решаемых через уравнения Лагранжа 2-го рода.

Эти уравнения удобны не только для решения отдельных задач динамики, но и для общетеоретических построений (теорий устойчивости, малых колебаний и других).

25. Уравнения возможных работ и мощностей в обобщённых силах

Уравнение возможных работ было получено ранее и имеет вид

.

Делим левую и правую части записанного уравнения на вариацию -той обобщённой координаты (на ). Получающиеся отношения называют: - -тая внешняя обобщённая сила; - -тая внутренняя обобщённая сила; - -тая обобщённая сила инерции.

В результате получим уравнения возможных работ и мощностей в обобщённых силах

.

Условие равновесия механической системы в обобщенных координатах

Согласно принципу возможных перемещений для системы с идеальными связями:

Учитывая что

получим

условие равновесия механической системы в обобщенных координатах.

Для равновесия механической системы необходимо и достаточно, чтобы все обобщенные силы соответствующие выбранным обобщенным координатам были равны нулю.

26. Уравнения лагранжа 2-го рода для консервативных систем

Консервативные – это системы, в которых действуют только потенциальные силы (и внешние, и внутренние).

Кинетический потенциал (иначе: функция Лагранжа) – это величина, определяемая разностью кинетической ( ) энергии системы и потенциальной ( ), т.е. .

Потенциальная энергия системы – это сумма потенциальных энергий всех частиц системы:

.

Потенциальная энергия является функцией лишь координат и, поэтому, для любой ( -той) частицы справедливо:

.

Возможное изменение потенциальной энергии -той частицы, соответствующее одновременной вариации всех обобщённых координат:

.

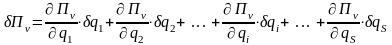При одиночной вариации -той обобщённой координаты возможное изменение потенциальной энергии равно:

, т.е.

.

Ранее было получено, что ( ), тогда : -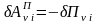

Возможная работа потенциальных сил (внутренних и внешних), приложенных к - той частице от одиночной вариации -той обобщённой координаты, равна взятой со знаком «минус» вариации потенциальной энергии этой же частицы и соответствующая той же одиночной вариации

. .

Полученное выражение подставляем в уравнение Лагранжа:

Учитывая то, что

( есть функцияобобщённых координат, но не скоростей), окончательно получаем

уравнения Лагранжа 2-го рода через кинетический потенциал:

.

Для составления уравнений Лагранжа нужно:

1. Изобразить на чертеже все активные силы, действующие на систему, если имеются силы трения, то их следует присоединить к активным силам;

2. определить число степеней свободы и ввести обобщенные координаты;

3. вычислить кинетическую энергию системы, выразив её через обобщенные координаты и скорости;

4. Составить уравнения работ и найти обобщенные силы системы;

5. выполнить указанные в уравнении Лагранжа действия