19. Силовое поле и силовая функция. Критерии потенциальности силового поля. Потенциальная энергия. Потенциальная энергия силы упругости. Закон сохранения полной механической энергии материальной точки

Силовым полем называют часть физического пространства, в каждой точке которого на рассматриваемую материальную точку действует сила, зависящая от координат рассматриваемой точки и времени, но не от скорости.

Силовое поле называется стационарным, если его силы не зависят от времени, нестационарным – если зависят.

Силовое поле является потенциальным, если существует такая функция , что

; ; .

Функция называется силовой и определяется в общем случае, с точностью до некоторой постоянной 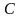, следующим образом: .Силы называются потенциальными, если они не зависят от характера движения точки.Элементарная работа силы на перемещении точки из положения М₀ в положение М:

, т.е.

.

Элементарная работа силы равна полному дифференциалу силовой функции.Значения работы и силовой функции отличаются на величину постоянной:

.

Критерии потенциальности силового поля

Как было указано ранее, для потенциального силового поля справедливо следующее:

; ; .

Отсюда следует, что

; и т.д.

Так как и т.д., то ; и .

К потенциальным силовым полям относятся поля: сил тяжести, сил упругости, сил тяготения. К непотенциальным (вихревым) полям относят поля: сил сопротивления, сил трения и т.д.

Множество точек для которых силовая функция будет одинакова и равняться некоторой постоянной (U=С) образуют поверхность уровня.

Свойства поверхностей уровня:

1) силы, действующие в силовом поле, будут всегда перпендикулярны к поверхностям уровня.

2) силы, действующие в силовом поле, будут направлены в сторону возрастания силовой функции.

Силовыми линиями (линиями уровня) называют такие линии, к которым являются касательными силы.

По определению параллельности векторов 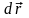и уравнения силовых линий будут иметь следующий вид: .

Определение силовых функций

Поле сил тяжести (ось направлена вертикально вверх).

.

Поверхности уровня – плоскости параллельные Земле.

Поле сил упругости.

.Поверхности уровня – сферы..

Потенциальной энергией называется работа, производимая силами потенциального силового поля по перемещению точки из конечного положения в начальное.

.

Понятие потенциальной энергии появилось намного раньше, чем понятие силовой функции, поэтому чаще используется при решении задач именно понятие потенциальной энергии.

Из последней формулы следует, что

; ; ;

.

Потенциальная энергия силы тяжести (ось направлена вертикально вверх):

.

Потенциальная энергия силы упругости:

.

Закон сохранения полной механической энергии материальной точки

Полной механической энергией материальной точки называется величина Е равная сумме кинетической и потенциальной энергии точки. Т.е. .

С одной стороны .

С другой – .

Поэтому

или . Окончательно .

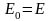Сумма кинетической и потенциальной энергий все время остается постоянной в потенциальном стационарном силовом поле.

Данный закон справедлив и для механической системы.

Этот закон является частным случаем закона сохранения энергии. Закон сохранения полной механической энергии не выполняется в непотенциальных (вихревых) полях. Закон сохранения полной механической энергии позволяет некоторые задачи динамики решать проще (без интегрирования и дифференцирования).