14. Лемма о полноте ив

Введем обозначения:F(x₁, x₂, …, x_n) – формула ИВ,x₁, x₂, …, x_n – список попарно различных переем-х, среди кот.есть все переем-е, входящие в ф-лу F.Пусть =<1, 2, …, n> – упорядоченный набор длины n из 0 и 1: i{0, 1}, .

F^σ=

Пр-р: Пусть F=x₁x₃;  = <0, 1, 1>, тогда . т.к. 01=1.. Если  = <1, 0, 0>, то

, т.к. 10=0.

Лемма (о выводимости).Для люб.ф-лы F(x₁, x₂, …, x_n) и люб.набора  справ-ива выводимость: x₁^, х₂^,…, х_n^ F^(x₁, x₂, …, x_n).Дано: Г={x₁^, х₂^, …х_n^}.Требуется док-ть, что Г F^.Док-во проведем м.м.и. по длине ф-лы F (числу логических связок k, входящих в запись ф-лы).Базис: k=0; F=x_i.Нужно док-ть: x₁^, х₂^, … x_i^, …, х_n^ F^=x_i^ – след-т по св-ву 1 вывод-сти из гипотез.Пусть для люб.ф-лы длины 0<k<s лемма выполняется. Р!ф-лу длины k=s.Возможны случаи:1) 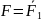2)F=F₁→F₂, F₁ и F₂ имеют длину меньше, чем s и для них утверждение леммы вып-ся, т.е. Г F₁^, Г F₂^. Требуется док-ть: Г F^.1) Рассмотрим 1–й случай: .Дано: Г F₁^.

Доказать: Г F^.Возможны 2 подслучая:

№	F1	F1σ	F	Fσ
a	0		1	F
b	1	F1	0

1 подслучай: а) Дано: Г F₁^= .

Док-ть: Г F^=F= .То, что требуется док-ть – дано.2 подслучай: б) Знач-е F₁ на  равно 1.

Дано: Г F₁^=F₁.

Док-ть: Г .

Требуемое след-т по з-ну введения дв.отрицания.Р!2–й случай:F=F₁→F₂.По индукционному предположению лемма считается верной для ф-л F₁ и F₂. Здесь возм. 4 подслучая:

	F1	F2	F1σ
a	0	0
b	0	1
c	1	0	F1
d	1	1	F1
	F2σ	F	Fσ
A		1	F
b	F2	1	F
c		0
d	F2	1	F

В каждом из подслучаев запишем, что дано и что требуется док-ть.

а) Дано: Г , Г Док-ть:

Г F₁F₂.1) Г дано. 2) Г, из 1) по 2. 3) Г, F₁ F₂ из 2) по О.К. 4) Г F₁F₂ из 3) по ТД. б) Дано: Г , Г F₂. Док-ть: Г F₁F₂. Док-во совпадает с пред. случаем. 1) Г дано 2) Г, из 1) по 2. 3) Г, F₁ F₂ из 2) по О.К. 4) Г F₁F₂ из 3) по ТД.

в) Дано: Г F₁, Г F₂,Док-ть: Г .Иначе, требуется до-ть: Г, F1, .Док-во:

1) Г, F1, F1F2 F2 МР к списку гипотез. 2) Г, F1, из 1) по П.К. 3) Г F₁ –дано. 4) Г, из 3), 4) по 3.5)Г –дано. 6) Г из 4), 5) по 3. г) Дано: Г F₁, Г F₂.

Док-ть: Г F₁F₂.Док-во: 1)Г F₂ дано 2)Г, F₁ F₂ из 1) по 2

Г F₁F₂ .из 2) по ТД.

Т.о., лемма справедлива для люб.ф-лы F.

13. Интерпретация ИВ. Непротиворечивость ИВ.(Связь ИВ с АВ)Пропозициональные перем-е б. истолковывать как выск-я, кот.принимают знач-я из мн-ва {0, 1}, логические связки ,  б. истолковывать как операции над выск-ми, определяемые теми же таблицами истинности, что и АВ, .Опр. Ф-ла ИВ наз-ся тавтологией или т.и.ф., если на люб.наборе знач-й переем-х она принимает значение 1 (истина).Лемма 1. Все аксиомы ИВ являются тавтологиями.Проверим аксиому А1: А(ВА). Построим таблицу истинности:

А	→	(В	→	А)
0	1	0	1	0
0	1	1	0	0
1	1	0	1	1
1	1	1	1	1

Также проверяются остальные аксиомы.Лемма 2. Правило вывода МР сохраняет тавтологичность ф-лы, т.е., если А и АВ – тавтологии, то В – тавтология.Док-во (методом от противного):Допустим, что В не явл-ся тавтологией, т.е. сущ-т набор значений переем-х, на кот.знач-е ф-лы В равно 0 (ложь), т.к. А – тавтология, то импликация АВ на наборе (1,0) ложна, т.к. В – ложна по допущению, что противоречит условию АВ – тавтология. След-но, ф-ула В – тавтология.

Отсюда след.теоремы:Т1. Если формула ИВ выводима, то она является тавтологией.

А А – Т.И.Ф.Док-во проведем м.м.и.Дано: ф-ла А – выводима из аксиом в ИВ, т.е. существует ее вывод:F₁, F₂, …, F_n=А – вывод А.Покажем что любая ф-ла вывода явл-ся ТИФ. Индукцию б.проводить по длине вывода ф-лы А.Построение базиса. Пусть n =1.F₁ – аксиома ( по лемме 1 – она тавтология).Индукционный шаг. Пусть док-но, что для nN, 1<n<k F_n явл-тся тавтологией.Док-м, что при n=k – Fk тавтология.

Для ф-лы Fk возможны случаи:

а) Fk – аксиома Fk – тавтология по лемме 1.б ) Fk получена по правилу МР из Fi и Fj (i, j<k) Fk – тавтология по лемме 2.

След-но, теорема справедлива nN.След-е: Если ф-ула не тавтология, то она в ИВ не выводима.Опр. ИВ наз-ся непротиворечивым, если не сущ-т ф-лы А такой, что одновременно в этом ИВ выводима она сама и ее отрицание, т.е. А и .Замечание: Требование непротиворечивости – важнейшее требование к мат.теории.

Т2. Исчисление выск-й непротиворечиво.Док-во: Допустим противное. Пусть ИВ – противоречиво, т.е. сущ-т ф-ла А такая, что А и . Т.к. А, то по Т1 она является тавтологией, но тогда тавтологией не явл-ся и поэтому она выводимой быть не может. Приходим к противоречию. Если ф-ла выводима, то она тавтология

12. З-ны прямой и обратной контрапозиции в исчислении выс-й. След. шагом на пути построения формализованного исчисл-я выск-й явл-ся выявл-е дальнейших закономерностей процесса выведения одних ф-л из др.и формулирование таких закономер-й в виде правил вывода. Получаемые вторичные правила вывода носят названия производных правил вывода (вторичных).Эти правила наз-ся правилами удаления или введения лог.связок. Введем новые лог.символы в качестве сокращения нек. Ф-л:

B A B –сокращ-е диз-цией

-сокращ-е кон-цией

Производные правила вывода:

1.Вв.→:

2.Уд.→:

3.Вв. :

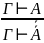
4.Уд. :

5. О.К.:

6. П.К.:

7.Вв.&:

8.Уд.&: Г, А&В А  Г, А&В В

9.Вв. : Г,А А В  Г, В А В

10.Уд. :

5)

1) Г, дано

2) →(А→В) (А3)

3) Г,А →(А→В) из 2) по 2

4) Г из 1) по ТД

5) Г, А из 4) по 2

6) Г, А из 3), 5) по МР

7) Г, А по 1

8) Г, А из 6), 7) по МР.

6)

1) Г, А В дано

2) В вв. 

3) Г, А из 1), 2) по 4˚

4) Г, А, из 3) по 2

5) Г, А уд. 

6) Г, из 4), 5) по 3

7) Г, из 6) по обрат. контр.

11..Правила введения и удаления двойного отрицания в исчислении выс-й. След. шагом на пути построения формализованного исчисл-я выск-й явл-ся выявл-е дальнейших закономерностей процесса выведения одних ф-л из др.и формулирование таких закономер-й в виде правил вывода. Получаемые вторичные правила вывода носят названия производных правил вывода (вторичных).Эти правила наз-ся правилами удаления или введения лог.связок. Введем новые лог.символы в качестве сокращения нек. Ф-л:

B A B –сокращ-е диз-цией

-сокращ-е кон-цией

Производные правила вывода:

1.Вв.→:

2.Уд.→:

3.Вв. :

4.Уд. :

5. О.К.:

6. П.К.:

7.Вв.&:

8.Уд.&: Г, А&В А  Г, А&В В

9.Вв. : Г,А А В  Г, В А В

10.Уд. :

Док-во:

3)

1) Г А дано

2) А→ пример 5

3) Г А→ из 2) по 2

4) Г из 1), 3) по МР.

4)

1) Г дано

2) →А пример 4

3) Г →А из 2) по 2

4) Г А из 1), 3) по МР.

10.Правила введения и удаления дизъюнкциив исчислении выс-й. След. шагом на пути построения формализованного исчисл-я выск-й явл-ся выявл-е дальнейших закономерностей процесса выведения одних ф-л из др.и формулирование таких закономер-й в виде правил вывода. Получаемые вторичные правила вывода носят названия производных правил вывода (вторичных).Эти правила наз-ся правилами удаления или введения лог.связок. Введем новые лог.символы в качестве сокращения нек. Ф-л:

B A B –сокращ-е диз-цией

-сокращ-е кон-цией

Производные правила вывода:

1.Вв.→:

2.Уд.→:

3.Вв. :

4.Уд. :

5. О.К.:

6. П.К.:

7.Вв.&:

8.Уд.&: Г, А&В А  Г, А&В В

9.Вв. : Г,А А В  Г, В А В

10.Уд. :

Док-во:

9) Анализ док-ва:Г, А А В;

Г,А →В; Г, А, В; Г, , .

Док-во:1) Г, , . по 1˚.

2) Г, А, В О.К. 3) Г,А →В Т.Д. 4) Г, А А В сокр. -ей.

10)

Анализ док-ва: Г, А В С; Г, →В С; Г, ; Док-во:

1) дано.

2) дано

3)Г, П.К. 1).

4) Г, П.К. 2).

5)Г, & из 3),4)-вв.&

6)Г, - расшифр. &

Продолжение анализа:

; ;

, ; ,

Продолж-е док-ва:

7) , МР к списку гипотез

8) , вв.

9) ТД

10) П.К.

11)Г, из 6),10) по 4˚

12)Г, →В С - О.К.

13)Г,А В С из 12) по сокр. -ей.

9.Правила введения и удаления конъюнкции в исчислении выс-й. След. шагом на пути построения формализованного исчисл-я выск-й явл-ся выявл-е дальнейших закономерностей процесса выведения одних ф-л из др.и формулирование таких закономер-й в виде правил вывода. Получаемые вторичные правила вывода носят названия производных правил вывода (вторичных).Эти правила наз-ся правилами удаления или введения лог.связок. Введем новые лог.символы в качестве сокращения нек. Ф-л:

B A B –сокращ-е диз-цией

-сокращ-е кон-цией

Производные правила вывода:

1.Вв.→:

2.Уд.→:

3.Вв. :

4.Уд. :

5. О.К.:

6. П.К.:

7.Вв.&:

8.Уд.&: Г, А&В А  Г, А&В В

9.Вв. : Г,А А В  Г, В А В

10.Уд. :

Док-во:

7)

Анализ док-ва:Г А&В, Г , Г, А, , Г, А, А →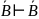 . Док-во:1) Г (дано). 2)Г В (дано). 3)Г, А, В, А→

МР к списку гипотез. 4)Г, А, В, , -П.К. 5)Г, А, В - вв. 6) Г, А, В из 4),5) по 3˚. 7)Г, В из 1),6)по 3˚. 8) Г из 2),7) по 3˚.9)Г . из 8 сокр.&-ей.

8) Г, А&В А

Анализ док-ва: Г, А&В А;

Г, ; Г, ;

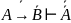Г, А→ ; Г, , А ; Г,В,А А. Док-во:1) Г,В,А А по 1˚. 2)Г, А П.К. 3)Г, А→ .

4) Г, П.К.

5). Г, А уд.

6).Г, А&В А сокращ.&-ей.

8. Теорема дедукции(Доказал венгерский математик ЭРБРАН).

Эта теорема позволяет упростить многие док-ва.Т. Если Г, А В, то Г АВ.

Суть теоремы закл-ся в след.: если из посылок А (мн-во гипотез Г м.б.пустым) выводимо по правилам логики нек. заключение В, то импликация АВ доказуема, т.е. выводима уже без всяких посылок, из одних аксиом,кот.явл-ся логически истинными предложениями. В процессе док-ва теорема позволяет вводить допущения, а потом освобождаться от них.Дано: дан вывод ф-улы В из Г, А.:(1)F₁, F₂, …, F_n=B.Док-ть: ф-ла АВ выводима из мн-ва гипотез Г.Док-во: Построим вспомогательную послед-ть ф- л:(2)АF₁,АF₂,…,АF_n=АB. Она заканчивается нужной нам ф-лой. Док-м, что дополнив послед-ть (2) некот. подходящими ф-лами, мы сможем получить из нее искомый вывод.Док-во б.проводить М.М.И. по длине вывода n ф-лы В.

I. Построение базиса мат. индукции.Пусть n=1.Дано: Г, А В, длина вывода ф-лы В равна 1, т.е. F₁=В.До-ть: выводима ф-ла АF₁ (Г АF₁).Возможны случаи: F₁ явл-ся либо аксиомой, либо гипотезой из Г, либо совпадает с А. Р!-м их. (Для опред-ти знак вывод-ти будем опускать).1) F₁ – аксиома. Требуется пол-ть: Г АF₁. Построим вывод:1.F₁аксиома

2.F₁(АF₁)(А1).3.АF₁, МР к 1, 2. В послед-ть (2) следует записать перед АF₁ формулы 1 и 2.2) F₁ – гипотеза из списка Г.1. F1-гипотеза, 2. F₁(АF₁) (А1)3. АF₁ МР к 1, 2. Вывод аналогичен предыдущему.3) F₁ совпадает с А. Надо док-: Г АА. Вывод ф-лы АА построен (см. пример 1 – 5 ф-л). По св-ву 2 м.записать Г АА.При n=1 теорема справедлива.

II. Индуктивный шаг.Предпол-м, что теорема дедукции верна для люб. n<k, т.е. для всех n<k из Г АFn.Док-м, что тогда при n=k из Г АFk, или Г АВ.Возможны 4 случая:

1. Fk – аксиома. 2.Fk-гипотеза из Г.3.Fk совпадает с А.4.Fk получается из двух предыдущих формул Fi и Fj по правилу (МР).Первые три случая совпадают с пред.1. Fk -гипотеза.2. Fk(АFk) (А1)

3. АFk, МР к 1, 2.В посл-ть (2) следует записать перед АF₁ формулы 1 и 2.

Будем для определенности считать, что Fi – малая посылка, Fj – большая посылка. Следовательно, Fj=FiFk. Запишем посл-ть ф-л:А2: А(ВС)((АВ)(АС)). Сделаем переобозначение переем-х: В на Fi, С на Fk

1. А(Fi  Fk)((А Fi)(АFk)) (А2)

2. А(Fi  Fk) = А Fj по предположению: т.к. j<k

3. (А Fi)(АFk) МР к 1, 2.

4. А Fi по предположению: т.к. i<k

5. АFk МР к 3, 4.

В посл-сть (2) след-т вставить ф-лы 1 и 3, а остальные в ней уже есть. По принципу математической индукции теорема справедлива для любого натурального n: Г АFn=АB.