II. Геометрия

M – множество точек, прямых и плоскостей.

P(x)=u Û x – точка.

L(x)=u Û x – прямая.

Pl(x)=u Û x – плоскость.

I(x, y)=u Û x инцидентно y.

1. Через любые две точки можно провести прямую.

"x "y (P(x) & P(y) ® $z (L(z) & I(x, z) & &I(y, z))).

2. Прямая x параллельна прямой y.

x||y Û p(x,y)Û L(x)&L(y)&$z(Pl(z) &

&I(x,z) &I(y,z) & &"vP(v)(I(x, v)® ØI(y,v))).

3. Существуют параллельные прямые. $x,$y p(x, y).

4. Прямые x и y скрещивася.Ск(x,y)Û L(x)&L(y)&$Øz(Pl(z)&I(x, z)&I(y, z)).

16. Понятие предиката. Способы задания предикатов. Примеры предикатов. Сигнатура. Определение формулы ЛП данной сигнатуры. Свободные и связанные переменные.

«Всякое целое число – рациональное число;

1 – целое число;

следовательно 1 – рациональное число». (*)

«Всякий ромб – параллелограмм;

ABCD – ромб;

следовательно ABCD – параллелограмм».(**)

«Из p и q следует r».

(ЛВ) не отличает высказывание, выражающее свойство предмета от высказывания, выражающего отношение между предметами

субъект (подлежащее)

предикат (сказуемое)

«ромб есть параллелограмм»

«ромб» – субъект

«параллелограмм» – предикат

«есть» – связка

«Число 3 меньше числа 5»

«Точка А лежит между точками В и С»

«S есть P», где S –субъект, P– предикат.

Понятие n – местного предиката и n –местной операции. Примеры

М – произвольное множество

n – кой элементов из множества М называется упорядоченный набор элементов этого множества.

Обозначение: <а1, а2, …, аn>, где а1, а2, …, аn ÎМ.

Определение. n – местным отношением (или n –местным предикатом на множестве М называется подмножество n – ок элементов этого множества.

Р(а1, а2, …, аn)=И

М╞Р(а1, а2, …, аn)Ûdef<а1, а2, …, аn>ÎP

в М истинен предикат Р

Способы задания предикатов

1. М – конечно: перечислением n – ок, принадлежащих этому предикату.

М={1, 2, 3, 4, 5}.

Р1={<1, 2>, <2, 3>, <1, 5>}.

М╞Р1(2, 3)

М╞Р1(3, 4).

2. М – бесконечно: предикат может быть задан высказыванием с переменными (или высказывательной формой).

Например: а) «х и y взаимно просты» – предикат на множестве N;

б) «х любит y» – предикат на множестве М – людей.

3. Предикат может быть задан уравнением или неравенством:

Р2(х1, х2, х3)=И Û на N.

N╞Р2(4, 5, 3).

Р3(х, y)=И Û на R.

R╞Р3(2, 1); R╞Р3(1, 2).

Р4(х, y, z, n)=И Û 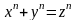на N.

N╞Р4(3, 4, 5, 2).

Р(х)=И Û х – простое число на N

Область значений предметной переменной х (N) называется областью определения предиката Р: N╞Р(5) и N╞Р(4)

2, 3, 5, 7, 11, 13, … обращают Р(х) в истинное высказывание

1, 4, 6, 8, 9, 10, … обращают Р(х) в ложное высказывание

Подмножество, на котором предикат принимает значение И называется областью истинности этого предиката

n – местная операция

Определение. n – местной операцией f на множестве М называется (n+1)–местный предикат со свойством функциональности: для любых х1, х2, …, хn, принадлежащих М существует единственный элемент yÎM, такой, что <х1, х2, …, хn, y>Îf.

y=f(х1, х2, …, хn)

Операции над предикатами

М: Р(х) и Q(x).

ØР(х)

Р(х)&Q(x)

Р(х)ÚQ(x)

Р(х)®Q(x)

Р(х)«Q(x)

1.ØР(х)

2. Р(х)&Q(x)

3. Р(х)ÚQ(x)

4. Р(х)®Q(x)

5. Р(х)«Q(x)

Р(х)®Q(x) )~ ØР(х) ÚQ(x)

Кванторы

Р(х1, х2, …, хn), где Р – символ предиката, х1, х2, …, хn – предметные переменные а1, а2, …, аn

Р(а1, а2, …, аn) - истинное или ложное n – ка предметов <а1, а2, …, аn> Операции связывания кванторами (или навешивания кванторов)

В первом случае истинно высказывание: «Для всех х (из М) имеет место (истинно) Р(х)», во втором – высказывание «Существует х (из М) такое, что Р(х) истинно».

Выражение «для всех х» («для любого х», «для всякого х») называется квантором общности и обозначается символом ("х).

Выражение «существует х такое, что…» называется квантором существования и обозначается символом ($х).

связанная переменная

Например, если Р(х) – предикат: «х – простое число» на множестве N, то ("х)Р(х) – ложное высказывание «Всякое натуральное число х – простое», а ($х)Р(х) – истинное высказывание «Существует натуральное число х такое, что оно простое».

Квантор общности можно рассматривать как обобщение конъюнкции, а квантор существования – как обобщение дизъюнкции.

М - область определения предиката Р(х)

М={а1, а2, …, аn}

("х)Р(х) равносильно конъюнкции

Р(а1)&Р(а2)&…&Р(аn)

($х)Р(х) равносильно дизъюнкции

Р(а1)ÚР(а2)Ú…ÚР(аn).

Если предикат Р(х) определен на бесконечном множестве, то кванторы играют роль «бесконечных» конъюнкций и дизъюнкций.

Определение формулы логики предикатов данной сигнатуры (сигнатура –signum – знак)

Алфавит:

1. x, y, z, …, - предметные (индивидные) переменные;

2. P1^(k1), P2^(k2), …, - список символов предикатов - предикатная сигнатура;

3. f1^(m1), f2^(m2), … - список символов операций;

4. ®, Ø, &, Ú - логические связки;

5. $, " - кванторы;

6. ( ,), , - три технических символа;

7. C1, C2, …, - символы констант.

Сигнатура термы

s=<P1^(k1), P2^(k2), …; f1^(m1), f2^(m2), …; C1, C2, …>

Опр.:

1. отдельно стоящая переменная – терм, отдельно стоящая const – терм;

2. если t1, …, tn – термы данной сигнатуры и f(n) – символ операции из данной сигнатуры, то f(t1, …, tn) – терм этой же сигнатуры;

3. других термов нет.

$x, "x

Опр.:

1. Если t1, t2 – термы данной сигнатуры, то t1=t2 – формула данной сигнатуры.

2. Если t1, …, tn – термы данной сигнатуры и P(n) – символ предиката из данной сигнатуры, то P(t1, …, tn) – формула данной сигнатуры.

3. Если A – формула данной сигнатуры, то 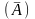- формула той же сигнатуры.

4. Если A и B – формулы данной сигнатуры, то (AÚB), (A&B), (A®B) являются формулами той же сигнатуры.

5. Если A(x) – формула сигнатуры s, содержащая x свободно, то выражения "xA(x), $xA(x) – формулы той же сигнатуры.

6. Других формул нет.