18. Проблемы выполнимости, общезначимости в тождественной ложности формул логики предикатов. Связь между этими проблемами. Т. Черча (без док-ва).

Опр.1: Формула F(x1, x2, …, xn) сигнатуры s называется общезначимой общезначимой (тождественно истинной) в данной модели, если она истинна в этой модели при любых значениях свободных переменных x₁, x₂, …, x_n.

Опр.2: Формула F(x₁, x₂, …, x_n) сигнатуры s называется общезначимой в широком смысле, если она истинна в любой модели той же сигнатуры на любых наборах значений свободных переменных, взятых из этой модели.

Пример: M, s=<P⁽²⁾>, F(x)= "y (P(x, y)ÚØP(x, y)) – истинна в любой модели данной сигнатуры (общезначима в широком смысле).

Опр.3: Формула F(x1, x2, …, xn) называется выполнимой в данной модели, если существует такой набор a₁, a₂, …, a_n элементов из этой модели, что F(x₁, x₂, …, x_n) истинна в этой модели на этом наборе элементов.

Опр.4: Формула F(x₁, x₂, …, x_n) называется выполнимой (в широком смысле), если существует такая модель и такие элементы a1, a2, …, an из этой модели, на которых эта формула истинна.

Опр.5: Формула F(x1, x2, …, xn) называется тождественно ложной (в широком смысле), если она ложна в любой модели на любых элементах из этой модели.

Т.: Проблемы общезначимости и выполнимости равносильны.

Замечание 1: Формула F(x1, x2, …, xn) общезначима

тогда и только тогда, когда формула Ø F(x1, x2, …, xn) является невыполнимой.

Пусть F(x1, x2, …, xn) общезначима. Возьмем произвольную модель , a1, a2, …, anÎM.

╞ F(a1, a2, …, an). Тогда

╞ ØF(a1, a2, …, an).

Это означает, что Ø F(x1, x2, …, xn) – тождественно ложная.

Замечание 2. F(x1, x2, …, xn) выполнима тогда и только тогда, когда формула Ø F(x1, x2, …, xn) не является общезначимой.

Доказательство. Пусть F(x1, x2, …, xn) – формула, которую мы хотим проверить на выполнимость. Применим замечание 2, т.е. решим проблему общезначимости для формулы Ø F.

Если Ø F - не общезначимая, то F - выполнимая.

17. Понятие модели данной сигнатуры и истинности формулы на модели.

s=<P1^(k1), P2^(k2), …; f1^(m1), f2^(m2), …; C₁, C₂, …>

Опр.Моделью данной сигнатуры

или алгебраической системой наз-ся непустое мн-во М вместе с заданными на этом мн-ве предикатами, операциями и константами соответствующими символами, предикатов, операций и констант данной сигнатуры. Мн-во М наз-ся носителем модели.

-сама модель

=<M, s>

=<M, P1^(k1),P2^(k2), …;f1^(m1),f2^(m2), …; C₁,С₂…>

1=<N, +> - аддитивная полугруппа натуральных чисел

2=<Z, +> - аддитивная группа целых чисел

3=<R, +, ×, £> - упорядоченное поле действительных чисел

Если в модели используется символы операции +,*, нет отношения порядка, то алгебра <M, +, × >

Пусть - модуль сигнатур F(x1, x2, …, xn)-ф-ла той же сигнатуры

╞F(a1, a2, …, an)

1) F(x1, x2, …, xn) совпадает с P(x1, x2, …, xn)

╞F(a1, a2, …, an) Ûопр.<a1, a2, …, an>Î P

2) (F1ÚF2), (F1&F2), (F1®F2), (ØF1)

3) "xF1(x, x1, x2, …, xn)

╞ "xF1(x,a1,a2,…,an) Û "bÎM

╞ F1(b, a1, a2, …, an)

4) $xF1(x, x1, x2, …, xn)

╞ $xF1(х,a1,a2,…,an) Û $bÎM

╞ F1(b, a1, a2, …, an)

Примеры записи математических предложений формулами логики предикатов

I. Арифметика.

Пусть N – множество натуральных чисел с нулем. N={0, 1, 2, ...}.

Рассмотрим два предиката:

S(x, y, z)=u Û x+y=z.

P(x, y, z)=u Û x×y=z.

=<N, S⁽³⁾, P⁽³⁾>, s=<S⁽³⁾, P⁽³⁾>

1. x=1;

2. х – четное число;

3. x=2;

4. y\x;

5. x – простое число;

6. x, y – простые числа близнецы;

7. x<y;

8. $ бесконечно много простых чисел близнецов.

1. e(x)=и Û x=1 Û"y (y×x=y) Û "y P(y, x, y).

2. Ч(x)=и Û $y S(y, y, x).

3. x=2 Û x=1+1 Û $z (z=1 & x=z+z) Û

$z (z=1 & S(z, z, x)) Û $z(e(z) & S(z, z, x))Û $z "y (P(y, z, y) & S(z, z, x)).

4. D(x, y)=и Û y\x Û $z (y×z=x) Û $z P(y, z, x).

5. Pr(x)=и Û x¹1 & ("y "z P(y, z, x) ® e(y)eÚ(z)) Û 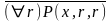&(("y)("z)(P(y, z, x) ® (("u) P(y, u, u)Ú("v) P(z, v, v)))).

6. Б(x, y)=и Û Pr(x) & Pr(y) & (y-x=2) Û

Pr(x) & Pr(y) & $z (z=2 & S(x, z, y)) Û

Pr(x) & Pr(y) & ($z $t e(t) & S(t, t, z) & S(x, z, y)).

7. x<y Û $z (x+z=y) Û $z S(х, z, y).

8. "z$x$yБ(x, y)&$tS(z, t, x).

Истинность этой формулы не известна

Т.1: Сложение натуральных чисел коммутативно.

"x "y "u (S(x, y, u) ® S(y, x, u)).

"x, y Î N

(x+y=y+x)

Пусть x+y=u,

тогда y+x=u.

Т.2: Сложение натуральных чисел ассоциативно.

"x "y "z "u "v "w

(S(x, y, u) & S(u, z, v)&

S(y, z, w) ® S(x, w, v))

"x, y, z

((x+y)+z=x+(y+z)).

Обозн.: x+y=u

y+z=w

u+z=v

x+w=v

u, v, w