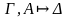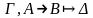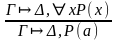19. Метод Генцена для решения проблемы выполнимости формул логики предикатов.
Метод служит для
проверки формул предикатов на общ-сть
или выполнимость. Он представляет собой
удобный способ записи рассуждений от
противного и использует определение
истинности формулы в модели. Будем при
записи использовать
разделяющий истинное от ложных: слева
И, справа Л функции.
Примеры:
Проверить на
тождественную истинность формулу:
,
где A
и B
– произвольные формулы.
Пусть утверждение об общезначимости неверно, т.е. формула ложна при некоторых значениях A и B.
(
®)
(
Ú)
(Ø
)
(
Ø)
(
)
*
противоречие
(
Ø)
*
противоречие
Преобразование формул по методу Герцена:
Как удалять истинную операцию |
|||
Обозн. |
Правило |
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
Подст. Дост. Одн. значения |
|
||
Подст. Множ. |
|
||
Как удалять истинную операцию |
|||
Обозн. |
Правило |
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
Подст. Множ.
|
|
||
Подст. Дост. Одн. значения |
|
||
Замечание 1. а – «новый» элемент, не встречавшийся ранее в данном соотношении («числителе») (левое $-правило и правое "-правило).
Замечание 2. а1, а2, … аn – элементы, уже встречавшиеся в данном соотношении («числителе») (правое $-правило и левое "-правило).
Замечание 3. Если в левой части соотношения встречаются формулы "х Р(х) и $х Q(х), то преобразование или анализ лучше начинать с формулы $х Q(х).
Замечание 4. Если в правой части соотношения встречаются формулы "х Р(х) и $х Q(х), то преобразование или анализ лучше начинать с формулы "х Р(х).
Замечание 5. Если слева формула "х Р(х), справа "х Q(х), то преобразование или анализ лучше начинать с формулы "х Q(х).
Замечание 6. Если слева формула $х Р(х), справа $х Q(х), то преобразование или анализ лучше начинать с формулы $х P(х).
Замечание 7. Может случиться, что при применении правил ( , $) и (", ) в данное соотношение «старые» элементы не входят. Тогда «искусственно» вводят «новый» элемент. Например, ( , $) - правило может быть записано так:
Г D, $х Р(х)
Г D, Р(а), $х Р(х).
Замечание 8. Правило из замечания 7 используется в последнюю очередь.
При применение метода Генцона могут возникнуть три случая:
1°. Появляются во всех подслучаях противоречия. Это означает, что первоначальное предположение неверно.
2°. В одном из подслучаев противоречие не возникает (см. предыдущий пример). Значит можно построить модель, в которой предположение выполняется.
3°. Алгоритм работает бесконечно. Ответа на поставленный вопрос мы не получаем.