22. Построение исчисления предикатов: алфавит, формула, аксиомы. Правила вывода, опр. Вывода формулы и вывод из гипотез в ип. Теорема Лп. Непротиворечивость ип.
I. Алфавит:
1. x, y, …, z, ... – индивидные переменные;
2. ®,Ø – логические связки;
3. P1(k1), P2(k2), …, - список символов предикатов с указанием их местности;
4. $, " - кванторы;
5. ( ,), , - три технических символа.
II. Определение формулы такое же как в ЛП.
III. Аксиомами назовем формулы вида:
(А1): А®(В®А);
(А2):А®(В®С)®((А®В)®(А®С)) – закон самодистрибутивности импликации;
(А3):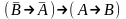
– закон контрапозиции.
(А4): "х А(х) ® А(t) (" – удаление)
(А5): А(t) $®х А(х) ($ - введение)
IV. Правила вывода:
1).
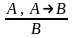– (MP).
2).
–
$
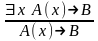– удаление;
3)
–
"
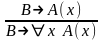– введение (правило обобщения), если х
не входит свободно в формулу В;
4) переименование свободной переменной, не являющейся связанной переменной этой формулы;
5) переименование связанной переменной.
V.Определение вывода формулы такое же как в ИВ, но добавляются новые правила вывода.
Определение вывода из гипотез остается в силе.
VI. Все теоремы, доказанные в (ИВ) остаются верными в (ИП).
Замечание: при доказательстве ТД следует включить еще пункты, связанные с новыми правилами вывода.
Две теоремы ИП
Т1. Если формула А выводима в ИП, то А – тавтология.
План доказательства:
Каждая аксиома ИП является тавтологией (с помощью метода Генцена).
По правилам вывода из тождественно истинных формул получаются снова тождественно истинные формулы.
Применяем индукцию.
Определение непротиворечивости такое же как в ИВ.
Следствие: Исчисление предикатов непротиворечиво.
Т2. Если формула тавтология, то она выводима в ИП. Доказательство: методом Генцена. (Курт Гёдель).
21. Предваренная нормальная форма (пнф), ее нахождение.
Опр. ПНФ называется формула, имеющая вид:
,
где
,
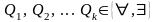причем формула F(x1, x2, …, xn) не содержит импликаций и кванторов. Отрицания относятся только к простейшим формулам, входящим в F. Q1x1 Q2x2 … Qkxk - кванторная приставка (префикс). F(x1, x2, …, xn) называется матрицей.
Пример:
1)
–
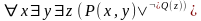ПНФ;
2)
–
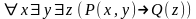не ПНФ, но легко написать равносильную
ей ПНФ:
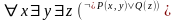
Т. Для любой формулы ЛП существует равносильная ей ПНФ
Чтобы найти ПНФ, нужно:
1) А®B ~ ØAÚB;
2) законы де Моргана;
3) равносильности (3)-(10); 4) ДНФ.
Пример: найти ПНФ, равносильную данной:
1)
-
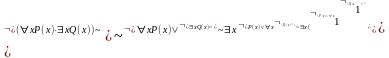
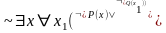ПНФ ДНФ
2)
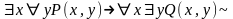
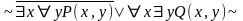
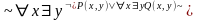
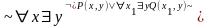
не содержит х
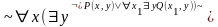
не содержит х1
–
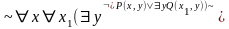
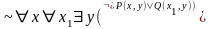ПНФ.
20. Основные равносильности лп, их док-во.
Опр. Две формулы F1 и F2 сигнатуры s называются равносильными, если они в любой модели той же сигнатуры на любых наборах элементов из этой модели принимают одинаковые значения истинности, т.е. в одной и той же модели они одновременно истинны либо одновременно ложны.
Обозн.: F1 ~ F2.
Замечание: Если формулы равносильны в АВ, то они равносильны и в ЛП, т.к. таблицы истинности остаются прежними.
Например:
ØØ"хР(x,y) ~ "хР(x,y);
ØP(x)&ØQ(y) ~ Ø(P(x)ÚQ(y)).
Равносильности ЛП
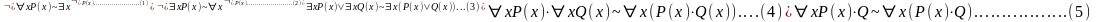
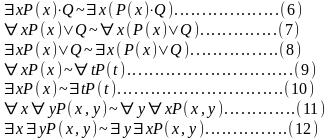
Формулы доказываются методом Генцена.
Замечания:
1) Формулы
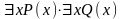и
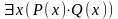
не равносильны, но из истинности второй следует истинность первой. Обратное неверно.
2) Формулы
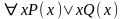и
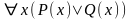
не равносильны, но из истинности первой следует истинность второй. Обратное неверно.
3) Формулы
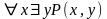и
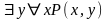
не равносильны, но из истинности второй следует истинность первой. Обратное неверно.