
- •23. Понятие об элементарных теориях.
- •Синтаксическое определение элементарных теорий.
- •22. Построение исчисления предикатов: алфавит, формула, аксиомы. Правила вывода, опр. Вывода формулы и вывод из гипотез в ип. Теорема Лп. Непротиворечивость ип.
- •21. Предваренная нормальная форма (пнф), ее нахождение.
- •20. Основные равносильности лп, их док-во.
- •19. Метод Генцена для решения проблемы выполнимости формул логики предикатов.
- •18. Проблемы выполнимости, общезначимости в тождественной ложности формул логики предикатов. Связь между этими проблемами. Т. Черча (без док-ва).
- •17. Понятие модели данной сигнатуры и истинности формулы на модели.
- •II. Геометрия
- •15. Полнота ив
- •14. Лемма о полноте ив
- •7.Вывод формул из гипотез
- •5.Применение основ.Равносильностей ал-ры выск-й.
- •4. Понятие о полноте системы булевых функций
4. Понятие о полноте системы булевых функций
Опр.
Сис-ма булевых ф-ций наз-ся полной, если
любую булеву ф-цию м.получить из ф-ций
дан.сис-мы с пом-ю операций подстановки
ф-ции в ф-цию и замены переем-х, примененных
конечное число раз.Основные лог.связки,
используемые нами – &, ,
,.
С помощью равносильности xy
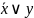 мы м.во всех ф-лах, в кот.встр-ся под.ф-ла
xy
заменить ее на
и, тем самым, исключить из использования
знак .Т1
С-ма булевых ф-ций {&, ,
}
явл-ся полной.Люб. булеву ф-кцию м.записать
в СДНФ. (н-р табличным способом).Т2
С-ма булевых ф-кций {,
}
явл-ся полной.
мы м.во всех ф-лах, в кот.встр-ся под.ф-ла
xy
заменить ее на
и, тем самым, исключить из использования
знак .Т1
С-ма булевых ф-ций {&, ,
}
явл-ся полной.Люб. булеву ф-кцию м.записать
в СДНФ. (н-р табличным способом).Т2
С-ма булевых ф-кций {,
}
явл-ся полной.
Следует
из Т1
и з-нов де Моргана:
![]()
![]() ,
,
![]()
![]()
Т3
С-ма булевых ф-кций {&, }
явл-ся полной.
Т3
С-ма булевых ф-кций {&, }
явл-ся полной.![]() .
.
Т4
Сис-а булевых ф-ций {,}
явл-ся полной.Следует из Т2
и равносильности xy
 .Т5
С-ма булевых ф-ций {&, ,},
не содержащая ,
не является полной.До-во: Р! булеву ф-цию
специального вида. Назовем ф-цию (или
формулу (АВ)) f(x1,x2,…,xn)
сохраняющей истину, если f(1,1,…,1)=1.
.Т5
С-ма булевых ф-ций {&, ,},
не содержащая ,
не является полной.До-во: Р! булеву ф-цию
специального вида. Назовем ф-цию (или
формулу (АВ)) f(x1,x2,…,xn)
сохраняющей истину, если f(1,1,…,1)=1.
Док-м,
что булевы ф-ции &, ,
сохраняют истину. Пусть f1(x1,x2,…,xn)
и f2(x1,x2,…,xn)
– ф-ции, сохраняющие истину, т.е. f1(1,
1,…,1)=1 и f2(1,
1,…,1)=1. Тогда:f1
& f2=1;f1
f2=1;f1
f2=1.Т.е.
булевы ф-ции &, ,
сохраняют истину, если они применяются
к ф-циям, сохраняющим истину. Других же
ф-ций получить нельзя.Но среди булевых
ф-кций есть ф-ции, не сохраняющие истину.
Н-р:
![]()
![]() .
.
Эту ф-цию нельзя получить с пом-ю рассматриваемой системы булевых ф-ций {&, ,}.
Следствие: Сис-мы булевых ф-ций {&, }, {&,}, {,}, {&}, {}, {} неполны. (Как подсистемы неполных систем).
Т6
Сист-ма булевых ф-ций {}
неполна.Пусть даны пропозициональные
переем-е x1,
x2,
…,.xn.
При помощи отрицания можно получить
только x1,
x2,
…,.xn,
 ,
т.е. ф-ции от одной переем-й и ни одной
ф-ции с двумя переем-ми. Это док-т
неполноту этой сис-мы.
,
т.е. ф-ции от одной переем-й и ни одной
ф-ции с двумя переем-ми. Это док-т
неполноту этой сис-мы.
Вместе с тем сущ-т полные сис-мы, содерж.одну булеву ф-цию, кот.выражается через &, , .
Штрих Шеффера
Обозн. xy (читается «x штрих y). Задается таблицей истинности:
![]()
Высказывание АВ озн-т, что А и В несовместны, т.е. не явл-ся истинными одновр-но. Через штрих Шеффера выраж-ся все др.лог.операции:x xx;
xy (xx)(yy);
x&y (xy)(xy);
xy x(yy).
x |
y |
xy |
xx |
yy |
|
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
0 |
|
xxyy |
xyxy |
x(yy) |
|||
0 |
0 |
1 |
|||
1 |
0 |
1 |
|||
1 |
0 |
0 |
|||
1 |
1 |
1 |
|||
Значит справедлива теорема 7:
Т7 Система булевых ф-ций {} явл-ся полной.Штрих Шеффера был введен в рассмотрение Г.Шеффером.Cтрелка Пирса (введена за 30 лет до ш.Шеффера).Обозн. x↓y (читается «x стрелка y»). Задается таблицей истинности:
![]()
Высказывание А↓В означает «ни А, ни В». Через стрелку Пирса выражаются все другие логические операции:
x x↓x;
x&y (x↓x)↓(y↓y);
xy (x↓y)↓(x↓y);
x |
y |
x↓y |
x↓x |
y↓y |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
(x↓x)↓(y↓y) |
(x↓y)↓(x↓y) |
((x↓x)↓y)↓((x↓x)↓y) |
||
0 |
0 |
1 |
||
0 |
1 |
1 |
||
0 |
1 |
0 |
||
1 |
1 |
1 |
||
((x↓x)↓y)↓((x↓x)↓y) Значит справедлива теорема 8:
Т8 Система булевых функций {} является полной
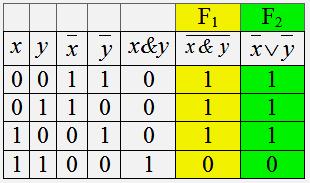
3. Основные равнос-сти алгебры выс-й.Равносильные ф-лыОпр. Две ф-лы алгебры выс--й наз-ся равносильными, если они на одинаковых наборах знач-й своих переем-х принимают одинаковые знач-я истинности. Обозн. F1F2
Читается: ф-ла F1 равносильна ф-ле F2.
Например: F1=x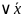 &y;
F2=x
y
&y;
F2=x
y
 .Свойства
логических операций:(Основные
равносильности (АВ))Приведем перечень
наиболее важных равносильных ф-л,
выражающих св-ва лог.операций,
непосредственно усматриваемых из опр-й
этих операций или легко устанавливаемых
с пом-ю таблиц истинности:
.Свойства
логических операций:(Основные
равносильности (АВ))Приведем перечень
наиболее важных равносильных ф-л,
выражающих св-ва лог.операций,
непосредственно усматриваемых из опр-й
этих операций или легко устанавливаемых
с пом-ю таблиц истинности:
1.
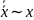 -закон
двойного отрицания.
-закон
двойного отрицания.
2. x&x x-идемпотентность конъюнкции.
3. xx x-идемпотентность дизъюнкции.
4. x&y y&x-ком-ть конъюнкции.
5. xy yx-коммутативность дизъюнкции.
6. (x&y)&z x&(y&z) -ассоциативность конъюнкции. 7. (xy) z x (yz) –ас-ть дизъюнкции.
8. x&(yz) (x&y)(x&z) -дистрибутивность конъюнкции относительно дизъюнкции.
9. x(y&z) (xy)&(xz) -дистрибутивность дизъюнкции относительно конъюнкции
10. x&(yx) x-закон поглощения.
11. x(y&x) x-закон поглощения.
12.
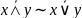 -.закон
де Моргана.
-.закон
де Моргана.
13 --закон де Моргана.
14. xy yx.
15. xy (xy)&(yx)
16.
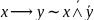 .
.
17
18. x&y
 .
.
19. xy
20.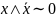 (
(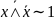 -закон
противоречия).
-закон
противоречия).
21.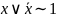 - закон исключенного третьего.
- закон исключенного третьего.
22. x&1 .
.
23. x .
.
24. x&0 .
.
25. x 0 x
Докажем формулу (12):
Равнос-сти м.испол-ть для упрощения ф-л алгебры выск-й.Н-р.
1)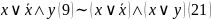
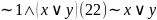
2)
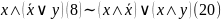
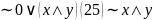
Дизъюнктивные и конъюнктивные нормальные формы.(ДНФ и КНФ).Для кажд.ф-лы ал-ры выс-й м. указать равносильную ей ф-лу, содержащую из лог.связок лишь отрицание, конъюнкцию и дизъюнкцию. Опр. Ф-ла F наз-ся элементарной конъюн-й (дизъюнкцией), если F есть кон-ция (диз-ция) простейших выск-й или их отрицаний, и кажд.простейшее выс-е встречается в ф-ле ровно один раз.
Пр-ры:
Элемент.кон-ция |
Элемент.диз-ция |
|
|
|
|
|
|
|
|
|
|
Опр. ДНФ (КНФ) наз-ся ф-ла, явл-ся дизъюнкц-й (конъюнкц-й) элем-х конъюнкций (дизъюнкций). Пр-ры: const. 0 –– ДНФ, xy – ДНФ,xy yzx – ДНФ.
Теорема. Всякая, не тождественно лож.ф-ла (АВ) равносильна нек-й ДНФ.Р! 2 способа нахождения ДНФ. Таб-й и аналитический (с помощью равносильностей).Пример. 1) Табличный:
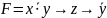 .
Составим т-цу истинности:
.
Составим т-цу истинности:
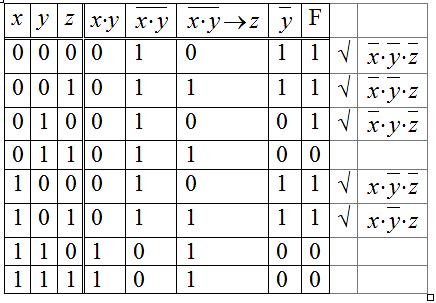
Рекомендации: выделить те строчки таблицы, в кот.значение ф-лы равно 1;напротив каждой выделенной строки записать конъюнкцию перем-х, входящих в ф- лу;поставить знак отрицания над теми перем-ми, значения кот.на дан.наборе равны 0;составить дизъюнкцию полученных элементарных конъюнкций. Это и есть ДНФ;
Упростить получ.ДНФ с пом-ю основных равносильностей до мин.ДНФ.
ДНФ:

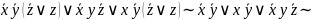 (
(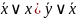 y
y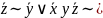 (
(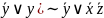
Аналитический:-избавиться от импликаций с помощью равнос-й;-используя з-ны де Моргана отрицания внести внутрь ф-лы так, чтобы они относились к перем-м, двойныеотрицания удалить; - с помощью дистрибутивного закона получить ДНФ;-упростить ДНФ.
Пример.
![]()
![]()
![]()
![]()
![]()
![]()
![]() – минимальная
ДНФ.
– минимальная
ДНФ.
Совершенная ДНФ
Опр. ДНФ называется совершенной отн-но дан.мн-ва переем-х, если каждая переем-я входит в каждую элементарную конъюнкцию (с отрицанием или без отрицания), причем ровно один раз.Элементарные конъюнкции, вход.в СДНФ д.б.различными.Н-р:
1) xyz xyz– СДНФ от x, y, z.
2) xy– СДНФ от x, y, но не является СДНФ от x, y, z.
Замечания 1. const.0 – СДНФ;
2. ДНФ, найденная табличным способом, является СДНФ.
3.
F=
– СДНФ от переменной x, но не является
СДНФ от x, y, z, которая может быть из нее
получена: F=![]() =
=![]() =
=![]() –
СДНФ от x, y, z.
–
СДНФ от x, y, z.
Теорема. Всякая ф-ла ал-ры выс-й имеет равносильную ей СДНФ, кот.опр-ся с точ-ю до порядка записи элемент-х конъюнкций.
2. Понятие булевой функции. Таблица истинности формулыПодставляя в ф-лу вместо пропозициональных пер-x, y, z,… значения 0,1, и выполняя действия, мы б.пол-ть знач-я ф-лы.Опр. Булевой ф-цией наз-ся ф-ция, зад. на мн-ве {0,1} и приним.знач-я из этого же мн-ва.Каждой ф-ле алгебры в-й соответствует булева ф-ция и притом единственная. Таблица знач-й этой ф-ции наз-ся таблицей истинности.Лемма. Сущ. 2n наборов, элементами кот-х явл-ся нули и единицы, длины n. (Длина набора – число символов, входящих в набор).Док-во методом математической индукции:
1. Пусть n=1: Имеем 2 набора {0},{1}.
2. Предположим, что утверждение леммы справедливо для n=k. Существует 2k наборов длины k, элементами кот-х явл-ся нули и единицы.
![]()
![]() {0,1}
{0,1}
Применим к набору (1) след. преобразование: сначала допишем в конце набора 0, а затем 1. В рез-те, из одного набора длины k получим два набора длины (k+1).
![]()
Таким же образом поступим с каждым из 2k наборов. Всего наборов получится:22k=2k+1.По принципу мат.индукции утверждение леммы справ-во для люб.нат.числа n.Теорема. Существует 22n булевых функций от n переменных.Р!булевы ф-ции от 2 пер-х:
x |
y |
f0 |
f1 |
f2 |
f3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
f4 |
f5 |
f6 |
f7 |
f8 |
f9 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
f10 |
f11 |
f12 |
f13 |
f14 |
f15 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
f00 – константа, f1=x&y – конъюнкция
f2=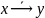 ,
f3=x
– повторение аргумента x, f4=
,
f3=x
– повторение аргумента x, f4=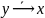 ,f5=y
– повторение аргумента y, f6=
,f5=y
– повторение аргумента y, f6=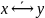 ,
f7=xy
– дизъюнкция. f8=
,
f7=xy
– дизъюнкция. f8=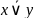 – стрелка Пирса, f9=xy
– эквивалентность, f10=
– инверсия y, f11=yx
– импликация,f12=
– инверсия x, f13=xy
– импликация,f14=
– стрелка Пирса, f9=xy
– эквивалентность, f10=
– инверсия y, f11=yx
– импликация,f12=
– инверсия x, f13=xy
– импликация,f14=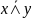 – штрих Шеффера,f151
– константа. Среди перечисленных 16-ти
ф-ций две ф-ции – константы, 4 ф-ции
зависят от одной пер-й и 10 – от 2-х.Особую
роль играют булевы ф-ции тождественно
рав.1 при люб.наборах знач-й пер-х.
– штрих Шеффера,f151
– константа. Среди перечисленных 16-ти
ф-ций две ф-ции – константы, 4 ф-ции
зависят от одной пер-й и 10 – от 2-х.Особую
роль играют булевы ф-ции тождественно
рав.1 при люб.наборах знач-й пер-х.
Опр. Формула (АВ) наз-ся тождественно истинной (тавтологией), если она принимает значение «истина» при люб.знач-х переем-х, входящих в ф-лу.
Пример: F(x,y)=(xy) (yx)
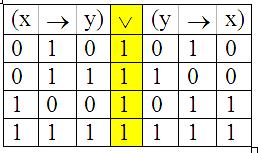
1.ВЫСКАЗЫВАНИЯ.Алгебра
высказываний.Высказывания и операции
над нимиВыс-е–основное,неопределяемое
понятие.Любые утверждения,об ист-ти
или лож-ти кот-х имеет смысл говорить,
мы б.наз-ть высказываниями,
при этом мы можем не знать, истинно ли
данное выс-е или нет. Выс-ми, например,
б.след. утверждения:- «Кама является
одной из крупнейших рек России»;- «8 –
есть простое число»;- «9000 –я цифра в
десятичной записи числа π есть 7». Первое
из этих утвержд-й истинно,второе–ложно;
ист-ть или лож-ть третьего утверж-я нам
неизвестна.Выс-я б.обоз-ть лат.буквами
(прописными и строчными, с индексами и
без них): A, B, C, ..., A1, A2, C3, …,p, q, r, …, q2, q3 …
.Итак, пусть p, q, r –выс-я или пропозициональные
(высказывательные) переменные,
кот.м.принимать два значения истинности:
Л (0; F – false) и И (1; Т – true). Разл. образом
сочетая выс.-я м\д собой, мы м.пол-ть
новые выс-я. Н-р, из двух выс-й: «Пермь –
столица Пермского края» и «8 – есть
простое число» м.пол-ть
след.выс-я:-«Пермь–столица Перм. края
и 8 – есть пр. число»,- «Пермь – столица
Пермского края или 8 – есть простое
число»,- «Если Пермь – столица Пермского
края, то 8 – есть простое число»,- «Пермь
– столица Пермского края тогда и только
тогда, когда 8 – есть простое число».Из
перв.выс-я м. получить новое выс-е -
«неверно, что Пермь является столицей
Пермского края», т.е. выс-я, явл.отрицанием
первого.Приведенные сочетания выс-й
образуются при помощи слов «И»; «ИЛИ»,
«ЕСЛИ…, ТО», «ТОГДА И ТОЛЬКО ТОГДА,
КОГДА…», «НЕ». В математической логике
для обозначения этих основных типов
сочетаний, имеющих название, используются
спец.символы:p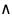 q(p&q,
pq,p∙q)–
читается «пэ и ку») – обозначает сложное
выс-е, истинное только в том случае,
когда p и q оба истинны. Такое выс-е
называют конъюнкцией (от лат. conjunctio –
союз, связь) высказываний p и q. p
q(читается
«пэ или ку») обозначает сложное выс-е,
истинное тогда лишь, когда по крайней
мере одно из выс-й истинно (м.быть
истинными оба выс-я). Такое выс-е наз-т
дизъюнкцией (от лат. disjunctio – различение,
разобщение) высказываний p и q.p
q(p
q,
p
q(p&q,
pq,p∙q)–
читается «пэ и ку») – обозначает сложное
выс-е, истинное только в том случае,
когда p и q оба истинны. Такое выс-е
называют конъюнкцией (от лат. conjunctio –
союз, связь) высказываний p и q. p
q(читается
«пэ или ку») обозначает сложное выс-е,
истинное тогда лишь, когда по крайней
мере одно из выс-й истинно (м.быть
истинными оба выс-я). Такое выс-е наз-т
дизъюнкцией (от лат. disjunctio – различение,
разобщение) высказываний p и q.p
q(p
q,
p q)–
читается «если пэ, то ку», «пэ достаточно
для ку», «ку необходимо для пэ», «ку с
необходимостью следует из пэ», «из пэ
следует ку», «пэ влечет ку») обозначает
сложное выс-е, кот.ложно только в том
случае, когда p истинно, а q ложно и
истинно во всех остальных случаях.
Такое выс-е называют импликацией (от
лат. implico – тесно связываю) выс-й p и q. В
импликативном высказывании p
q
различают антецедент (основание) –
высказывание p и консеквент (следствие)–выс-е
q.p
q)–
читается «если пэ, то ку», «пэ достаточно
для ку», «ку необходимо для пэ», «ку с
необходимостью следует из пэ», «из пэ
следует ку», «пэ влечет ку») обозначает
сложное выс-е, кот.ложно только в том
случае, когда p истинно, а q ложно и
истинно во всех остальных случаях.
Такое выс-е называют импликацией (от
лат. implico – тесно связываю) выс-й p и q. В
импликативном высказывании p
q
различают антецедент (основание) –
высказывание p и консеквент (следствие)–выс-е
q.p q(p
q(p q,
p
q,
p
q,
p
q,
p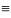 q)–
читается «пэ тогда и только тогда, когда
ку», «пэ если и только если ку», «пэ в
том и только том случае, когда ку»)
обоз-т сложное выс-е, истинное, когда
выс-я p и q одновременно оба истинны или
оба ложны. Такое выс-е наз-т эквивалентностью
выс-p и q.
–
читается «не пэ», «неверно, что пэ») –
есть противоположность p. Обозначает
выс-е, истинное, если p ложно и ложное,
если p истинно. Такое выс-е наз-т отрицанием
высказывания p.Замечание 1. Символы
&,
,
,
соответствуют
бинарным операциям: новое высказывание
сопоставляют двум высказываниям p и q,
а символ
выражает определенную на том же мн-ве
унарную операцию: сопоставляет новое
высказывание одному высказыванию
p.Замечание 2. Слова «и»; «или», «если…,
то», «тогда и только тогда, когда…»,
являющиеся связками в нашем обычном
языке, в мат.логике получают несколько
иной смысл.В обычном языке союз «и»
исп-ся, как правило, для объединения
двух предложений, соответствующих друг
другу по смыслу в некот.связном
повествовании как это бывает при
описании последовательности событий
(Елена хорошо подготовилась к экзамену
Однако в логике «И» м.соединять
люб.предл-я, совершенно незав-мо от
наличия смыслового соответствия м\д
ними.Аналог.союз ИЛИ в обычном языке
употребляется в двух смыслах – в смысле
исключающем от лат. aut («p или q, но не
оба») и в смысле неисключающем от лат.
vel («p или q, или оба). Именно в последнем
смысле мы б.исп-ть союз ИЛИ чаще. И здесь
опять несущественна смысл.зав-ть
соединяемых выс-й.Не сущ-на смысловая
связь в логике между выс-ми и при
построении импликации, хотя в обычном
языке сложное предл-е «если p, то q»
предп-т м\д p и q отн-е посылки и следствия,
или же причины и обусловленного ею
дей-я.(Если б. дождь, то мы не пойдем на
прогулку).В логике для ис-ти импликации
дост-но, чтобы p было ложно или q –
истинно.Т.о.,выс-я типа:– Если 7 – простое
число, то 22=4;–
Если 8 – простое число, то 22=4;-Если
8 – простое число, то 22=5
д.считаться истинным.
Утверждение «p тогда и только тогда,
когда q» не означает в логике, что
составляющие предл-я p и q имеют одно и
то же знач-е или один и тот же смысл, оно
означает лишь выск-е, кот.истинно, когда
оба выс-я истинны или ложны.Все, что
говорилось о лог.смысле конъюнкции,
дизъюнкции,импликации, эквивалентности
и отрицания м.просто и наглядно
проиллюстрировать с пом-ю Т.Н.таб-ц
истинности.В таблицах выпис-ся
всевозможные комбинации ист-х и лож-х
зн-й составл.выс-й, а в результирующей
колонке указ-ся ист-ть или лож-ть сложного
выс-я для кажд.такой комбинации.
Б.сопоставлять ист-му выс-ю символ 1, а
ложному – символ 0.Вот как выглядят
т-цы истинности для &,
,
,
и
:
q)–
читается «пэ тогда и только тогда, когда
ку», «пэ если и только если ку», «пэ в
том и только том случае, когда ку»)
обоз-т сложное выс-е, истинное, когда
выс-я p и q одновременно оба истинны или
оба ложны. Такое выс-е наз-т эквивалентностью
выс-p и q.
–
читается «не пэ», «неверно, что пэ») –
есть противоположность p. Обозначает
выс-е, истинное, если p ложно и ложное,
если p истинно. Такое выс-е наз-т отрицанием
высказывания p.Замечание 1. Символы
&,
,
,
соответствуют
бинарным операциям: новое высказывание
сопоставляют двум высказываниям p и q,
а символ
выражает определенную на том же мн-ве
унарную операцию: сопоставляет новое
высказывание одному высказыванию
p.Замечание 2. Слова «и»; «или», «если…,
то», «тогда и только тогда, когда…»,
являющиеся связками в нашем обычном
языке, в мат.логике получают несколько
иной смысл.В обычном языке союз «и»
исп-ся, как правило, для объединения
двух предложений, соответствующих друг
другу по смыслу в некот.связном
повествовании как это бывает при
описании последовательности событий
(Елена хорошо подготовилась к экзамену
Однако в логике «И» м.соединять
люб.предл-я, совершенно незав-мо от
наличия смыслового соответствия м\д
ними.Аналог.союз ИЛИ в обычном языке
употребляется в двух смыслах – в смысле
исключающем от лат. aut («p или q, но не
оба») и в смысле неисключающем от лат.
vel («p или q, или оба). Именно в последнем
смысле мы б.исп-ть союз ИЛИ чаще. И здесь
опять несущественна смысл.зав-ть
соединяемых выс-й.Не сущ-на смысловая
связь в логике между выс-ми и при
построении импликации, хотя в обычном
языке сложное предл-е «если p, то q»
предп-т м\д p и q отн-е посылки и следствия,
или же причины и обусловленного ею
дей-я.(Если б. дождь, то мы не пойдем на
прогулку).В логике для ис-ти импликации
дост-но, чтобы p было ложно или q –
истинно.Т.о.,выс-я типа:– Если 7 – простое
число, то 22=4;–
Если 8 – простое число, то 22=4;-Если
8 – простое число, то 22=5
д.считаться истинным.
Утверждение «p тогда и только тогда,
когда q» не означает в логике, что
составляющие предл-я p и q имеют одно и
то же знач-е или один и тот же смысл, оно
означает лишь выск-е, кот.истинно, когда
оба выс-я истинны или ложны.Все, что
говорилось о лог.смысле конъюнкции,
дизъюнкции,импликации, эквивалентности
и отрицания м.просто и наглядно
проиллюстрировать с пом-ю Т.Н.таб-ц
истинности.В таблицах выпис-ся
всевозможные комбинации ист-х и лож-х
зн-й составл.выс-й, а в результирующей
колонке указ-ся ист-ть или лож-ть сложного
выс-я для кажд.такой комбинации.
Б.сопоставлять ист-му выс-ю символ 1, а
ложному – символ 0.Вот как выглядят
т-цы истинности для &,
,
,
и
:
p |
q |
P&q |
p q |
P
q |
p q |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Понятие
формулы алгебры выс-й.Опр.
Алфавитом наз-ся произв.мн-во символов.
Введем алфавит, сост.из след. групп
символов:x, y, z, p, …А, В,… – пропозициональные
переем-е;&,
,
,
и
:–
лог.связки;(, ) – 2 технических символа.Опр.
(ф-лы алгебры выск-й):Каждая отдельно взятая
пропозицион-я перем-я есть ф-ла алгебры
выс-й. Ф-лы такого вида наз-ся простейшими
(атомами).Если x – формула ал-ры выс-й
(АВ), то (x)
– ф-ла (АВ).Если x и y – ф-лы ал-ры выс-й,
то (x&y), (xy),
(xy),
(xy)
– тоже ф-лы (АВ).Никаких др.ф-л (АВ), кроме
получающихся сог-сно п.п.1–3 нет.Опр-я
такого типа наз-ся индуктивными. В них
имеются прямые пункты (1,2,3), где задаются
объекты, к.в дальнейшем именуются
определяемым термином и косвенный
пункт (4), в к.говорится,что такие объекты
исчерпываются зад.в прямых пунктах.
Среди прямых пунктов им-тся базисные
(1), где указ-ся нек.конкретные объекты,
именуемые в дал.определяемым термином,
и индуктивные пункты (2,3), где даются
правила получения определяемых объектов
из уже имеющихся объектов, в частности
из объектов, перечисл-х в базисных
пунктах.Зам-е: «О силе связок».Для
упрощения записи формул (уменьшения
числа скобок в них) будем считать,
что:порядок выполнения лог.операций
над выс-ми д.б.след.:,
&, ,
,
внешние
скобки, заключающие внутри себя все
остальные символы, составл.ф-лу,
м.опускать.Учитывая это соглашение, а
также опустив знак конъюнкции, ф-лу
![]() м.зап-ть в виде
м.зап-ть в виде![]() .При
чтении ф-ла м.б.названа по «последней»
операции. Запис.ф-ла П.С. импл-цию.
.При
чтении ф-ла м.б.названа по «последней»
операции. Запис.ф-ла П.С. импл-цию.

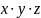
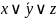
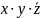
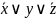
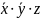
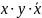 -не
явл-ся
-не
явл-ся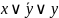 -не
явл-ся
-не
явл-ся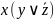 -не
явл-ся
-не
явл-ся -не
явл-ся
-не
явл-ся