Вопрос 3. Свободная энергия Гиббса, Гельмгольца. Условия самопроизвольного протекания процессов в изобарно-изотермических и изохорно-изотермических условиях.
Свободная энергия Гиббса.
Разность (H-TS) называют энергией Гиббса системы и обозначают буквой G. Энергия Гиббса термодинамическая функция состояния системы. Изменение энергии Гиббса deltaG=deltaH-TdeltaS.
Энергия Гиббса химической реакции характеризует направление и предел самопроизвольного протекания реакции в условиях постоянства температуры и давления.
Свободная энергия Гельмгольца.
Разность (U-TS) называют энергией Гельмгольца системы и обозначают F. Энергия Гельмгольца также является термодинамической функцией состояния системы. Изменение энергии Гельмгольца deltaF=deltaU-TdeltaS.
DeltaF характеризует направление и предел самопроизвольного течения реакции в изохорно-изотермических условиях.
Условия: В изохорно-изотермических – идет если F<= 0
В изобарно-изотермических – идет если G<= 0.
Билет №13
Вопрос 1. Полярность химической связи. Дипольный момент связи. Полярность и дипольный момент молекул.
Химическая связь - это взаимодействие двух атомов, осуществляемое путем обмена электронами. При образовании химической связи атомы стремятся приобрести устойчивую восьмиэлектронную (или двухэлектронную) внешнюю оболочку, соответствующую строению атома ближайшего инертного газа. Различают следующие виды химической связи: ковалентная (полярная и неполярная; обменная и донорно-акцепторная), ионная, водородная и металлическая.
Ковалентная связь
Если электронная плотность расположена симметрично между атомами, ковалентная связь называется неполярной.
Если электронная плотность смещена в сторону одного из атомов, то ковалентная связь называется полярной.
Полярность связи тем больше, чем больше разность электроотрицательностей атомов.
Дипольный момент связи
Дипольный момент связи (m) - векторная величина, характеризующая полярность связи: |m| = l·q, где l - длина связи, q - эффективный заряд, который приобретают атомы при смещении электронной плотности. Вектор дипольного момента направлен от положительного заряда к отрицательному.
Полярность и дипольный момент молекул.
При векторном сложении дипольных моментов всех связей получают дипольный момент молекулы. Молекулы с отличным от нуля дипольным моментом называются полярными.
2) Если потенциал металлического анода имеет более отрицательное значение, чем потенциал ионов OH или других веществ, присутствующих в растворе, в газовой фазе около электрода или на электроде, то происходит растворение металла. При этом протекает электролиз с растворимым анодом. Если потенциал металлического анода близок к потенциалу других электродных процессов, то наряду с растворением металла на аноде протекают также другие процессы, например разряд ионов OH. В этом случае также говорят об электролизе с растворимым анодом, но учитывают и другие анодные процессы. Если потенциал металла или другого проводника первого рода, используемого в качестве анода, имеет более положительное значение, то протекает электролиз с нерастворимым анодом. качестве нерастворимых анодов применяют золото и платиновые металлы, диоксид свинца, оксид рутения и другие вещества, имеющие положительные значения равновесных электродных потенциалов, а также графит. Некоторые металлы практически не растворяются из-за высокой анодной поляризации, например никель и железо в щелочном растворе, свинец в H2SO4, титан, тантал, нержавеющая сталь. Явление торможения анодного растворения металла из-за образования защитных слоев называется пассивностью металла.
При электролизе с нерастворимым анодом на электроде может окисляться ион OH, или другие ионы, или недиссоциированные молекулы восстановителей, присутствующие в растворе.
3) Зависимость скорости реакции от концентрации реагентов.
Чтобы произошла реакция, необходимо столкновение реагирующих частиц. При одной и той же температуре число столкновений растёт с увеличением числа реагирующих частиц в единице объёма, т.е. с возрастанием концентрации реагентов. Соответственно скорость реакции повышается с увеличением концентраций реагирующих веществ. Скорость необратимой реакции bB+dD=lL+mM
равна v=k*cB^nB*cD^nD (Серега советует переписать это на листик =))) )
где k-константа скорости реакции; nB и nD – коэффициэнты, называемые порядками реакции по веществам B и D. Уравнение называется кинетическим уравнением химической реакции.
Константа скорости реакции k не зависит от концентрации реагентов, но зависит от их природы и температуры. Из уравнения следует, что при cD=cB=1 (например, 1 моль/л) константа скорости реакции численно равна скорости реакции. Из этого же уравнения видно, что размерность константы скорости реакции зависит от порядка реакции, поскольку размерность скорости реакции для всех гомогенных реакций одинакова.
Например, для реакции диссоциации молекулы А2=2А для которой
v=kcА2 , (nA=1),
единицу измерения константы скорости реакции можно определить, исходя из анализа размерностей: [моль*л^-1*c^-1] = [x] * [моль*л^-1]. Соответственно [x]=[c^-1].
Итак, скорость реакции пропорциональна произведению концентраций реагентов в степенях, называемых порядками реакции по реагентам.
Основной постулат кинетики: Скорость реакции зависит от природы реагирующих веществ, их концентрации, температуры и наличия катализатора.
Зависимость скорости реакции от концентрации описывается основным постулатом химической кинетики - законом действующих масс: скорость химической реакции в каждый момент времени пропорциональна текущим концентрациям реагирующих веществ, возведенным в некоторые степени:
,
где k - константа скорости (не зависящая от концентрации); x, y - некоторые числа, которые называют порядком реакции по веществам A и B, соответственно. Эти числа в общем случае никак не связаны с коэффициентами a и b в уравнении реакции. Сумма показателей степеней x + y называется общим порядком реакции. Порядок реакции может быть положительным или отрицательным, целым или дробным.
Большинство химических реакций состоит из нескольких стадий, называемых элементарными реакциями. Под элементарной реакцией обычно понимают единичный акт образования или разрыва химической связи, протекающий через образование переходного комплекса. Число частиц, участвующих в элементарной реакции, называют молекулярностью реакции. Элементарные реакции бывают только трех типов: мономолекулярные (A B + ...), бимолекулярные (A + B D + ...) и тримолекулярные (2A + B D + ...). Для элементарных реакций общий порядок равен молекулярности, а порядки по веществам равны коэффициентам в уравнении реакции.
Одностадийные реакции.
Относительно небольшое число реакций протекает в одну стадию. К ним можно отнести, например
Реакции диссоциации
H2=2H, Cl2=2Cl, 2HI=H2+I2
Взаимодействие йода и водорода
I2+H2=2HI
Взаимодействие монооксида азота с водородом и озоном
2NO+H2=N2O+H2O
NO+O3=NO2+O2
Одностадийные реакции, как и сложные реакции, протекают, как правило через образование активированного комплекса. Для одностадийных реакций порядок реакций совпадает с молекулярностью реакции, т.е. мономолекулярные, бимолекулярные и тримолекулярные реакции являются соответственно реакциями первого, второго и третьего порядка. Кинетическое уравнение одностадийной химической реакции совпадает с законом действующих масс.
Сложные химические реакции.
К сложным относятся реакции, протекающие последовательно через несколько стадий, или параллельно. Большинство реакций являются многостадийными. Например, реакция
2А+3В=А2В3
Может идти через стадии
А+В=АВ (1)
А+АВ=А2В (2)
А2В+2В=А2В3 (3)
2А+3В=А2В3
Если одна из этих стадий будет протекать значительно медленнее других, то она будет определять скорость всего процесса, и её называют лимитирующей стадией. Скорость всей реакции будет определяться скоростью лимитирующей стадии. Например, если лимитирующй будет стадия (1), то скорость этой стадии и соответственно всей реакции будет равна v=k*cA*cB.
В данном случае n=1+1=2, т.е. порядок реакции меньше суммы стехиометрических коэффициентов (5). Обычно лимитирующая стадия записывается как необратимая реакция, а другие стадии как обратимые реакции. Например, реакция разложения пентаоксида азота N2O5
2N2O5=4NO2+O2
Протекает через следующие стадии
N2O5 >< (это типа 2 стрелочки, т.е. обратимая) NO2+NO3 (быстрая стадия)
NO2+NO3 > NO2+NO+O2 (медленная стадия)
NO+NO3 >< 2NO2 (быстрая стадия)
Первая стадия мономолекулярная, вторая и третья - бимолекулярные. Лимитирующей является вторая стадия. В ходе реакции образуются промежуточные короткоживущие частицы (интермедиаты) NO3 и NO2. Для нахождения уравнения скорости реакции принимают, что устанавливается стационарная концентрация промежуточных частиц на основании предположения, что скорость образования интермедиатов равна скорости их расходования. Вследствие такого предположения можно определить скорость лимитирующей стадии и соответственно скорость всей реакции. Например, определив концентрацию интермедиатов (NO2 и NO3), получим, что скорость второй стадии и соответственно скорости всей рассматриваемой реакции равна V=k*cN2O5
Как видно, порядок этой реакции (первый) меньше суммы стехиометрических коэффициентов (2). Порядок реакции (1) отличается от молекулярности второй и третьей стадий (2).
1) 1) Расчеты в квантовой механике производят с помощью предложенного в 1926 г. австрийским ученым Э. Шредингером уравнения, которое является математическим описанием электронного строения атома в трехмерном пространстве.
-(h²/8π²m)(∂²ψ/∂x² + ∂²ψ/∂y² + ∂²ψ/∂z²) + Uψ = Eψ
Решая уравнение Шредингера, находят волновую функцию ψ = f (x,y,z). Решение возможно лишь при определенных значениях полной энергии E. Определив вероятностную функцию ψ, можно оценить величину |ψ|²dV – вероятность нахождения электрона в объеме пространства dV, окружающего атомное ядро.
Как следует из решения уравнения Шредингера для атома водорода, квантовое состояние электрона в этом атоме (можно сказать и квантовое состояние атома) полностью определяется заданием трех квантовых чисел.
Каждое из квантовых чисел принимает только целочисленные значения и определяет, то есть предсказывает результаты измерения основных физических величин в заданном квантовом состоянии атома.
Главное квантовое число n определяет энергию электрона и размеры электронных облаков. Энергия электрона главным образом зависит от расстояния электрона от ядра: чем ближе к ядру находится электрон, тем меньше его энергия. Поэтому можно сказать, что главное квантовое число n определяет расположение электрона на том или ином энергетическом уровне (квантовом слое). Главное квантовое число имеет значения ряда целых чисел от 1 до ∞. При значении главного квантового числа, равного единице (n=1), электрон находится на первом энергетическом уровне, расположенном на минимально возможном расстоянии от ядра. Полная энергия такого электрона наименьшая.
Электрон, находящийся на наиболее удаленном от ядра энергетическом уровне, обладает максимальной энергией. Поэтому при переходе электрона с более удаленного энергетического уровня на более близкий выделяются порции (кванты) энергии.
Орбитальное квантовое число l. Электронные облака отличаются не только размерами, но и формой. Форму характеризует орбитальное или азимутальное квантовое число. Различная форма электронных облаков обусловливает изменение энергии электронов в пределах одного энергетического уровня, т.е. ее расщепление на энергетические подуровни. Принимает значение целых чисел от 0 до (n - 1). Независимо от номера энергетического уровня, каждому значению орбитального квантового числа соответствует орбиталь особой формы. Набор орбиталей с одинаковыми значениями n называется энергетическим уровнем, с одинаковыми n и l - подуровнем.
Для:
l=0 s-подуровень, s-орбиталь – орбиталь сфера.
l=1 p-подуровень, p-орбиталь – орбиталь гантель.
l=2 d-подуровень, d-орбиталь – орбиталь сложной формы
f-подуровень, f-орбиталь – орбиталь еще более сложной формы.
На первом энергетическом уровне (n = 1) орбитальное квантовое число l принимает единственное значение l = (n - 1) = 0. Форма обитали - сферическая; на первом энергетическом только один подуровень - 1s. Для второго энергетического уровня (n = 2) орбитальное квантовое число может принимать два значения: l = 0, s- орбиталь - сфера большего размера, чем на первом энергетическом уровне; l = 1, p- орбиталь - гантель. Таким образом, на втором энергетическом уровне имеются два подуровня - 2s и 2p. Для третьего энергетического уровня (n = 3) орбитальное квантовое число l принимает три значения: l = 0, s- орбиталь - сфера большего размера, чем на втором энергетическом уровне; l = 1, p- орбиталь - гантель большего размера, чем на втором энергетическом уровне; l = 2, d- орбиталь сложной формы.
Таким образом, на третьем энергетическом уровне могут быть три энергетических подуровня - 3s, 3p и 3d.
Магнитное квантовое число m характеризует положение электронной орбитали в пространстве и принимает целочисленные значения от -l до +l, включая 0. Это означает, что для каждой формы орбитали существует (2l + 1) энергетически равноценных ориентации в пространстве.
Для s-орбитали (l = 0) такое положение одно и соответствует m = 0. Сфера не может иметь разные ориентации в пространстве.
Для p-орбитали (l = 1) - три равноценные ориентации в пространстве (2l + 1 = 3): m = -1, 0, +1.
Для d-орбитали (l = 2) - пять равноценных ориентаций в пространстве (2l + 1 = 5): m = -2, -1, 0, +1, +2.
Таким образом, на s-подуровне - одна, на p-подуровне - 3, на d-подуровне - 5, на f-подуровне - 7 орбиталей.
2) 1-ое начало термодинамики. Теплота полученная системой, растрачивается на изменение внутренней энергии и на совершение работы.
Q = ∆U + A
1. Изолированная система. ∆U=0 Q=A
2. Изохорный (V=const) A=p∆V => A=0 Q= - ∆U
3. Изобарный (p=const) Qp = ∆U + p∆V
∆U = U2 – U1
∆V = V2 – V1
H = U + pV
1-ый физический смысл энтальпии – энергия расширенной системы.
H1 – H2 = ∆H ∆H = -Qp
2-ой смысл энтальпии – тепловой эффект реакции при постоянном давлении.
Hº298 - стандартная энтальпия одного или больше вещества, взятого из простых веществ при T = 298К и p = 1 атм. (101кПа).
Энтальпия простого вещества = 0
Энтальпией образования химического соединения называется изменение энтальпии в процессе получения моль этого соединения из простых веществ, устойчивых при данной температуре.
Стандартная энтальпия образования соединения – мера его термодинамической устойчивости, прочности, количественное выражение энергетических свойств соединения. Эта термодинамическая функция характеризуется периодичностью и может быть ориентировочно оценена для какого-либо соединения так же, как и любое другое свойство.
3.Стандартный водородный электрод(СВЭ).Сейчас за нуль принят потенциал СВЭ. Он относится к газовым электродам, т.е. к электродам, в котором по крайней мере один из реагентов является газообразным. Т.к. для протекания электродн. реакции необходим подвод и отвод электронов, то газовые электроды содержат проводники 1го рода. В качестве проводника 1го рода СВЭ служит платина. При контакте с молекулярным водородом происходит адсорбция водорода на платине. Адсорбированный водород переходит в раствор в виде ионов, оставляя в платине электроны. При этом платина заряжается отрицательно, а раствор – положительно. Возникает скачок потенциалов между платиной и раствором. Наряду с переходом ионов в раствор идёт обратный процесс восстановления ионов H(+) с образованием молекул водорода.
2H(+) +2е H2
Абсолютное значение потенциала водородного электрода неизвестно, но условно считают за нуль потенциал СВЭ т.е. пртенциал при pH2 =1 ( 101КПа) и aH+ =1 моль/л.
Билет №15
1) 1) Расчеты в квантовой механике производят с помощью предложенного в 1926 г. австрийским ученым Э. Шредингером уравнения, которое является математическим описанием электронного строения атома в трехмерном пространстве.
-(h²/8π²m)(∂²ψ/∂x² + ∂²ψ/∂y² + ∂²ψ/∂z²) + Uψ = Eψ
Решая уравнение Шредингера, находят волновую функцию ψ = f (x,y,z). Решение возможно лишь при определенных значениях полной энергии E. Определив вероятностную функцию ψ, можно оценить величину |ψ|²dV – вероятность нахождения электрона в объеме пространства dV, окружающего атомное ядро.
Как следует из решения уравнения Шредингера для атома водорода, квантовое состояние электрона в этом атоме (можно сказать и квантовое состояние атома) полностью определяется заданием трех квантовых чисел.
Каждое из квантовых чисел принимает только целочисленные значения и определяет, то есть предсказывает результаты измерения основных физических величин в заданном квантовом состоянии атома.
Главное квантовое число n определяет энергию электрона и размеры электронных облаков. Энергия электрона главным образом зависит от расстояния электрона от ядра: чем ближе к ядру находится электрон, тем меньше его энергия. Поэтому можно сказать, что главное квантовое число n определяет расположение электрона на том или ином энергетическом уровне (квантовом слое). Главное квантовое число имеет значения ряда целых чисел от 1 до ∞. При значении главного квантового числа, равного единице (n=1), электрон находится на первом энергетическом уровне, расположенном на минимально возможном расстоянии от ядра. Полная энергия такого электрона наименьшая.
Электрон, находящийся на наиболее удаленном от ядра энергетическом уровне, обладает максимальной энергией. Поэтому при переходе электрона с более удаленного энергетического уровня на более близкий выделяются порции (кванты) энергии.
Орбитальное квантовое число l. Электронные облака отличаются не только размерами, но и формой. Форму характеризует орбитальное или азимутальное квантовое число. Различная форма электронных облаков обусловливает изменение энергии электронов в пределах одного энергетического уровня, т.е. ее расщепление на энергетические подуровни. Принимает значение целых чисел от 0 до (n - 1). Независимо от номера энергетического уровня, каждому значению орбитального квантового числа соответствует орбиталь особой формы. Набор орбиталей с одинаковыми значениями n называется энергетическим уровнем, с одинаковыми n и l - подуровнем.
Для:
l=0 s-подуровень, s-орбиталь – орбиталь сфера.
l=1 p-подуровень, p-орбиталь – орбиталь гантель.
l=2 d-подуровень, d-орбиталь – орбиталь сложной формы
f-подуровень, f-орбиталь – орбиталь еще более сложной формы.
На первом энергетическом уровне (n = 1) орбитальное квантовое число l принимает единственное значение l = (n - 1) = 0. Форма обитали - сферическая; на первом энергетическом только один подуровень - 1s. Для второго энергетического уровня (n = 2) орбитальное квантовое число может принимать два значения: l = 0, s- орбиталь - сфера большего размера, чем на первом энергетическом уровне; l = 1, p- орбиталь - гантель. Таким образом, на втором энергетическом уровне имеются два подуровня - 2s и 2p. Для третьего энергетического уровня (n = 3) орбитальное квантовое число l принимает три значения: l = 0, s- орбиталь - сфера большего размера, чем на втором энергетическом уровне; l = 1, p- орбиталь - гантель большего размера, чем на втором энергетическом уровне; l = 2, d- орбиталь сложной формы.
Таким образом, на третьем энергетическом уровне могут быть три энергетических подуровня - 3s, 3p и 3d.
Магнитное квантовое число m характеризует положение электронной орбитали в пространстве и принимает целочисленные значения от -l до +l, включая 0. Это означает, что для каждой формы орбитали существует (2l + 1) энергетически равноценных ориентации в пространстве.
Для s-орбитали (l = 0) такое положение одно и соответствует m = 0. Сфера не может иметь разные ориентации в пространстве.
Для p-орбитали (l = 1) - три равноценные ориентации в пространстве (2l + 1 = 3): m = -1, 0, +1.
Для d-орбитали (l = 2) - пять равноценных ориентаций в пространстве (2l + 1 = 5): m = -2, -1, 0, +1, +2.
Таким образом, на s-подуровне - одна, на p-подуровне - 3, на d-подуровне - 5, на f-подуровне - 7 орбиталей.
2) Еакт- та избыточная (по сравнению со сред. Эн. Молекул) энергия, при которой протекают взаимодействия.
С повышением t возрастает кол-во молекул, облад энергией активации.
Энергия активации Еа равна разности энергий переходного и исходного состояний:
Еа = Еперех.сост. - Еисх.сост.
Чем меньше энергия активации реакции, тем выше ее скорость.
Для каждой реакции своя энергия активации
Аррениус разработал теорию «активных молекул»
Α=Nакт/Nобщ=е–Eакт/RT
K=A е–Eакт/RT
А – предэкспоненциальный множитель (коэф пропорциональности)
К – константа скорости реакции
3) Концентрационный гальванический элемент.
Концентрационные гальванические элементы
Особенностью концентрационного гальванического элемента, рис.4, является то, что оба электрода выполнены из одного и того же метала.
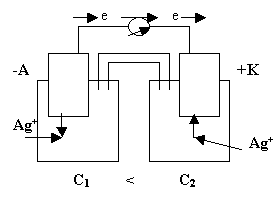
Рис.4
Эти электроды отличаются друг от друга только концентрациями солевых растворов.
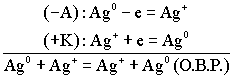
(По формуле Нерста) рассчитаем ЭДС концентрационного элемента.
Недостатки концентрационных гальванических элементов:
разрушаемый анод,
малая ЭДС.
Концентрационные элементы используются в тех случаях, где необходима малая ЭДС.
Окислительно - восстановительные (ОВ) гальванические элементы
Особенностью данных элементов является то, что окислительно - восстановительный процесс протекает только в растворах. Оба электрода являются инертными, или пассивными, т.е. сами они не принимают участия в ОВ процессах, а выполняют роль проводников электронов.
Билет №16
1) Правило Хунда: в данном подуровне электрон стремится занять энергетические состояния таким образом, чтобы суммарный спин был максимальным.
Принцип Паули: в атоме не может быть двух электронов, у которых были бы одинаковые все четыре квантовых числа. Из принципа Паули вытекает следствие: максимально возможное число электронов на каждом энергетическом уровне равно удвоенному значению квадрата главного квантового числа: x = 2πn².
Правило Клечковского: общий запас энергии, а значит и последовательное заполнение энергетических уровней происходит в порядке возрастания суммы чисел n + l, а при равных значениях n + l – в порядке возрастания n:
1s<2s<2p<3s<3p<4s≈3d<4p<5s≈4d<5p<6s≈5d≈4f<6p и т.д.
Поведение электронов в атомах подчиняется принципу запрета, сформулированному в 1925 г. В. Паули: в атоме не может быть двух электронов, у которых были бы одинаковые все четыре квантовых числа.
Согласно принципу Паули, на одной орбитали, характеризуемой определенными значениями трех квантовых чисел n, l и ml, могут находится только два электрона отличающихся значением спинового квантового числа ms, а именно ms = +1/2 и ms = -1/2. Действительно, если n = 1, то l и ml могут иметь только нулевые значения. Поэтому электроны с n = 1 могут отличаться только значением спинового квантового числа. Следовательно на первом энергетическом уровне могут находиться только два электрона. На втором энергетическом уровне электроны занимают два подуровня.
Из принципа Паули вытекает следствие: максимально возможное число электронов на каждом энергетическом уровне равно удвоенному значению квадрата главного квантового числа: x = 2πn².
Энергетические уровни и подуровни, которые содержат максимально допустимое число электронов, называют замкнутыми. Замкнутый s-подуровень (l=0) содержит 2 электрона, замкнутый p-подуровень (l=1) содержит 6 электронов, в замкнутом d-подуровне (l=2) находится 10 электронов, в замкнутом f-подуровне (l=3) – 14 электронов и т.д.
При заполнении электронами энергетических подуровней соблюдается правило Хунда: в данном подуровне электроны стремятся занять энергетические состояния таким образом, чтобы суммарный спин был максимальным.
2) Зависимость скорости реакции от концентрации реагентов.
Чтобы произошла реакция, необходимо столкновение реагирующих частиц. При одной и той же температуре число столкновений растёт с увеличением числа реагирующих частиц в единице объёма, т.е. с возрастанием концентрации реагентов. Соответственно скорость реакции повышается с увеличением концентраций реагирующих веществ. Скорость необратимой реакции bB+dD=lL+mM
равна v=k*cB^nB*cD^nD (Серега советует переписать это на листик =))) )
где k-константа скорости реакции; nB и nD – коэффициэнты, называемые порядками реакции по веществам B и D. Уравнение называется кинетическим уравнением химической реакции.
Константа скорости реакции k не зависит от концентрации реагентов, но зависит от их природы и температуры. Из уравнения следует, что при cD=cB=1 (например, 1 моль/л) константа скорости реакции численно равна скорости реакции. Из этого же уравнения видно, что размерность константы скорости реакции зависит от порядка реакции, поскольку размерность скорости реакции для всех гомогенных реакций одинакова.
Например, для реакции диссоциации молекулы А2=2А для которой
v=kcА2 , (nA=1),
единицу измерения константы скорости реакции можно определить, исходя из анализа размерностей: [моль*л^-1*c^-1] = [x] * [моль*л^-1]. Соответственно [x]=[c^-1].
Итак, скорость реакции пропорциональна произведению концентраций реагентов в степенях, называемых порядками реакции по реагентам.
Основной постулат кинетики: Скорость реакции зависит от природы реагирующих веществ, их концентрации, температуры и наличия катализатора.
Зависимость скорости реакции от концентрации описывается основным постулатом химической кинетики - законом действующих масс: скорость химической реакции в каждый момент времени пропорциональна текущим концентрациям реагирующих веществ, возведенным в некоторые степени:
,
где k - константа скорости (не зависящая от концентрации); x, y - некоторые числа, которые называют порядком реакции по веществам A и B, соответственно. Эти числа в общем случае никак не связаны с коэффициентами a и b в уравнении реакции. Сумма показателей степеней x + y называется общим порядком реакции. Порядок реакции может быть положительным или отрицательным, целым или дробным.
Большинство химических реакций состоит из нескольких стадий, называемых элементарными реакциями. Под элементарной реакцией обычно понимают единичный акт образования или разрыва химической связи, протекающий через образование переходного комплекса. Число частиц, участвующих в элементарной реакции, называют молекулярностью реакции. Элементарные реакции бывают только трех типов: мономолекулярные (A B + ...), бимолекулярные (A + B D + ...) и тримолекулярные (2A + B D + ...). Для элементарных реакций общий порядок равен молекулярности, а порядки по веществам равны коэффициентам в уравнении реакции.
Одностадийные реакции.
Относительно небольшое число реакций протекает в одну стадию. К ним можно отнести, например
Реакции диссоциации
H2=2H, Cl2=2Cl, 2HI=H2+I2
Взаимодействие йода и водорода
I2+H2=2HI
Взаимодействие монооксида азота с водородом и озоном
2NO+H2=N2O+H2O
NO+O3=NO2+O2
Одностадийные реакции, как и сложные реакции, протекают, как правило через образование активированного комплекса. Для одностадийных реакций порядок реакций совпадает с молекулярностью реакции, т.е. мономолекулярные, бимолекулярные и тримолекулярные реакции являются соответственно реакциями первого, второго и третьего порядка. Кинетическое уравнение одностадийной химической реакции совпадает с законом действующих масс.
Сложные химические реакции.
К сложным относятся реакции, протекающие последовательно через несколько стадий, или параллельно. Большинство реакций являются многостадийными. Например, реакция
2А+3В=А2В3
Может идти через стадии
А+В=АВ (1)
А+АВ=А2В (2)
А2В+2В=А2В3 (3)
2А+3В=А2В3
Если одна из этих стадий будет протекать значительно медленнее других, то она будет определять скорость всего процесса, и её называют лимитирующей стадией. Скорость всей реакции будет определяться скоростью лимитирующей стадии. Например, если лимитирующй будет стадия (1), то скорость этой стадии и соответственно всей реакции будет равна v=k*cA*cB.
В данном случае n=1+1=2, т.е. порядок реакции меньше суммы стехиометрических коэффициентов (5). Обычно лимитирующая стадия записывается как необратимая реакция, а другие стадии как обратимые реакции. Например, реакция разложения пентаоксида азота N2O5
2N2O5=4NO2+O2
Протекает через следующие стадии
N2O5 >< (это типа 2 стрелочки, т.е. обратимая) NO2+NO3 (быстрая стадия)
NO2+NO3 > NO2+NO+O2 (медленная стадия)
NO+NO3 >< 2NO2 (быстрая стадия)
Первая стадия мономолекулярная, вторая и третья - бимолекулярные. Лимитирующей является вторая стадия. В ходе реакции образуются промежуточные короткоживущие частицы (интермедиаты) NO3 и NO2. Для нахождения уравнения скорости реакции принимают, что устанавливается стационарная концентрация промежуточных частиц на основании предположения, что скорость образования интермедиатов равна скорости их расходования. Вследствие такого предположения можно определить скорость лимитирующей стадии и соответственно скорость всей реакции. Например, определив концентрацию интермедиатов (NO2 и NO3), получим, что скорость второй стадии и соответственно скорости всей рассматриваемой реакции равна V=k*cN2O5
Как видно, порядок этой реакции (первый) меньше суммы стехиометрических коэффициентов (2). Порядок реакции (1) отличается от молекулярности второй и третьей стадий (2).