5.2 Анализ по времени
Анализ по времени проводится функцией clock() из стандартной библиотеки <time.h>. Длины ребер задаем с помощью функции rand() из той же библиотеки <time.h>, длины этих ребер будут варьироваться от 0 до 99. Ниже на рисунке 14 представлена диаграмма роста функции f(t)=N, где t – время работы программы в секундах, а N – количество вершин. «Жирным» выделен график роста функции алгоритма Флойда, а «тонким» выделен график роста функции алгоритма Беллмана-Форда.
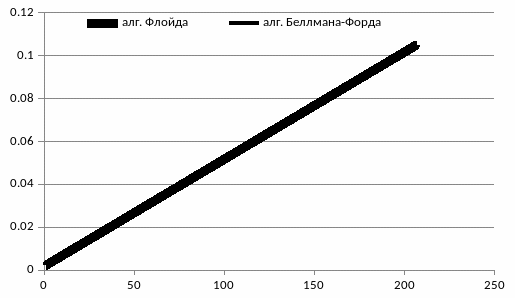
Рисунок 14 – Диаграмма роста функции f(t)=N
6 Анализ результатов
Проанализируем результаты, алгоритмы Флойда и Беллмана-Форда очень похожи по своей структуре и поиску кратчайших путей, они различаются по хранению промежуточной информации о кратчайших путях. Исходя из этого, они различаются и в скорости роста функции f(t)=N. Как показали тесты, эти два алгоритма схожи и в работе с ребрами отрицательного веса.
Заключение
Для достижения поставленной цели потребовалось реализовать алгоритмы Флойда и Беллмана-Форда в среде (программе) Microsoft Visual Studio. При создание кода программы использовалась программа Microsoft Visual Studio 2008. В результате при помощи созданной программы была получена возможность нахождения минимального расстояния между всеми вершинами, при случайном распределении длин ребер, при ручном вводе и вводе при помощи файла. Так же был изменен код алгоритма Беллмана-Форда, для того, чтобы этот алгоритм находил кратчайшие пути между всеми вершинами графа, а не от одной вершины до всех остальных. Проанализирована работа алгоритмов Флойда и Беллмана-Форда, после чего составлены диаграммы тестирования скорости работы, по которым можно сравнить работу алгоритмов.
Можно добавить, что поиск пути не тривиальная задача, существует несколько хороших, надежных, и всем известных алгоритмов, которые заслуживают должного внимания в сообществе разработчиков. Помимо представленных выше алгоритмов, хорошо известны такие алгоритмы как алгоритм Дейкстры, алгоритм Джонсона, все они решают одни и те же задачи, но подходы к решению отличаются.
Некоторые алгоритмы поиска пути не очень эффективны, но их изучение позволяет постепенно вводить концепции. Так можно понять, как решаются различные проблемы.
Список использованных источников
ГОСТ 7.32–2001. Отчёт о научно-исследовательской работе. Структура и правила оформления [Текст]. – Взамен ГОСТ 7.32–91 ; введ. 2001–07–01. – Минск : Межгос. совет по стандартизации, метрологии и сертификации ; М. : Изд-во стандартов, 2001. – 16 с. – (Система стандартов по информации, библиотечному и издательскому делу).
ГОСТ 7.1–2003. Библиографическая запись. Библиографическое описание. Общие требования и правила составления [Текст]. – Взамен ГОСТ 7.1–84, ГОСТ 7.16–79, ГОСТ 7.18–79, ГОСТ 7.34–81, ГОСТ 7.40–82 ; введ. 2004–07–01. – М. : Изд-во стандартов, 2004. – 116 с. – (Система стандартов по информации, библиотечному и издательскому делу).
Левитин А. В. Алгоритмы: ввдение в разработку и анализ. / А. В. Левитин ; пер. с англ. под общ. ред. С. Г. Тригуб. – М. : Издательский дом «Вильямс», 2006. – 576 с.
Макконелл Дж. Основы современных алгоритмов / Дж. Макконелл ; пер. с англ. под общ. ред. С. К. Ландо. – М. : Издательство ЗАО РИЦ «Техносфера», 2004. – 368 с.
Приложение А
(обязательное)