3 Анализ трудоемкости роста функции
Время выполнения программы по алгоритму Флойда состовляет O(n^3), так как в ней нет практически ничего, кроме 3 вложенных друг в друга циклов.
Наилучшим случаем для алгоритма станет граф в котором всего нет улучшения пути, т. е. вводимая матрица расстояний не изменится после выполнения программы. В этом случае время выполнения программы составит O(n^3).
Наихудшим случаем для алгоритма станет граф с отрицательным циклом. Если в графе есть циклы отрицательного веса, то формально алгоритм Флойда к такому графу неприменим. Но на самом деле алгоритм корректно сработает для всех пар, пути между которыми никогда не проходят через цикл негативной стоимости, а для остальных мы получим какие-нибудь числа, возможно сильно отрицательные. Алгоритм можно научить выводить для таких пар некое значение, соответствующее -∞.
В среднем случае алгоритм не будет иметь отрицательных циклов и улучшит почти все пути. Таким образом он не превысит an^3+bn^2+cn+d операций.
Анализ алгоритма Беллмана-Форда.
Время выполнения программы, имеет порядок O(nm), где n – это количество вершин, а m - это количество дуг.
Наилучшим случаем для алгоритма станет граф в котором 2 вершины и отсутствуют дуги, т. е. вводимая матрица расстояний состоит из нулей.
4 Программа реализации алгоритмов
Ниже проиллюстрирована работа алгоритма Флойда, а сам код написан в Приложении А. Заполнение матрицы расстояний осуществляем при помощи чтения текстового файла «algF .txt», заполненная матрица представлена на рисунке 11.
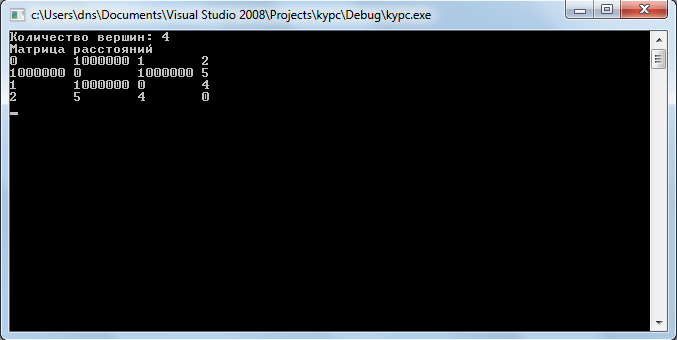
Рисунок 11 – Ввод матрицы из файла
На рисунке 12 представлен вывод матрицы кратчайших расстояний заданного графа, помимо матрицы показано время работы программы в секундах.
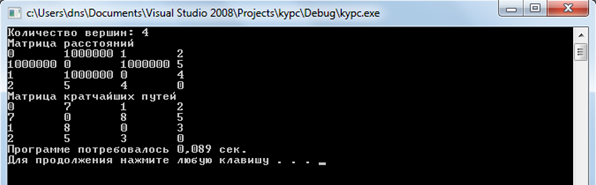
Рисунок 12 – Вывод результатов работы программы по алгоритму Флойда
На рисунке 13 показана матрица кратчайших путей, программа реализована с помощью алгоритма Беллмана-Форда. Заполнение матрицы расстояний осуществляем при помощи чтения текстового файла «algBF .txt» В том же рисунке показано время работы программы. Полный код программы находится в Приложении Б. В реализации этого алгоритма пришлось добавить внешний цикл, в котором будут пробегать все вершины: for(start_v=1;start_v<=n;start_v++), таким образом этот алгоритм теперь находит не от одной вершины до всех остальных, а от каждой вершины до всех остальных.
Рисунок 13 - Вывод результатов работы программы по алгоритму Беллмана-Форда
5 Тестирование программ реализации алгоритмов
5.1 Тестирование правильности
Протокол тестирования правильности работы программы по алгоритму Флойда содержится в таблице 1. В входных данных вводится матрица расстояний, так же матрицу ожидаем получить и в выходных данных. Будем считать, что несуществующее ребро между двумя вершинами будет равняться inf = 1000. Первый пример характеризует ориентированный граф, второй же неориентированный. В 3 - м случае граф состоит из 6 вершин. В 4 и 5 примерах используются ребра отрицательного веса, где последний задает граф с циклом отрицательного веса.
Таблица 1 – Тестирование правильности алгоритма Флойда
№ п/п |
Входные данные |
Выходные данные |
Тест |
|
Ожидаемый результат |
Действительный результат |
|||
Matr[N][N] |
Matr[N][N] |
Matr[N][N] |
||
1 |
0 inf 3 inf 2 0 inf inf inf 7 0 1 6 inf inf 0 |
0 10 3 4 2 0 5 6 7 7 0 1 6 16 9 0 |
0 10 3 4 2 0 5 6 7 7 0 1 6 16 9 0 |
+ |
Продолжение таблицы 1
2 |
0 inf 1 2 inf 0 inf 5 1 inf 0 4 2 5 4 0 |
0 7 1 2 7 0 8 5 1 8 0 3 2 5 3 0 |
0 7 1 2 7 0 8 5 1 8 0 3 2 5 3 0 |
+ |
3 |
0 7 9 inf inf 14 7 0 10 15 inf inf 9 10 0 11 inf 2 inf 15 11 0 6 inf inf inf inf 6 0 9 14 inf 2 inf 9 0 |
0 7 9 20 20 11 7 0 10 15 21 12 9 10 0 11 11 2 20 15 11 0 6 13 20 21 11 6 0 9 11 12 2 13 9 0 |
0 7 9 20 20 11 7 0 10 15 21 12 9 10 0 11 11 2 20 15 11 0 6 13 20 21 11 6 0 9 11 12 2 13 9 0 |
+ |
4
|
0 inf -3 inf 2 0 inf inf inf 7 0 1 6 inf inf 0 |
0 4 -3 -2 2 0 -1 0 7 7 0 1 6 10 3 0 |
0 4 -3 -2 2 0 -1 0 7 7 0 1 6 10 3 0 |
+ |
5 |
0 inf -3 inf 2 0 inf inf inf 7 0 -1 -6 inf inf 0 |
В графе есть цикл отрицательного веса. |
В графе есть цикл отрицательного веса. |
+ |
Протокол тестирования правильности работы программы по алгоритму Беллмана-Форда содержится в таблице 2. В входных данных вводится матрица расстояний, так же матрицу ожидаем получить и в выходных данных. Будем считать, что несуществующее ребро между двумя вершинами будет равняться inf = 1000. Первый пример характеризует ориентированный граф, второй же неориентированный. В 3 - м случае граф состоит из 6 вершин. В 4 и 5 примерах используются ребра отрицательного веса, где последний задает граф с циклом отрицательного веса.
Таблица 2 – Тестирование правильности алгоритма Беллмана-Форда
№ п/п |
Входные данные |
Выходные данные |
Тест |
|
Ожидаемый результат |
Действительный результат |
|||
Matr[N][N] |
Matr[N][N] |
Matr[N][N] |
||
1 |
0 inf 3 inf 2 0 inf inf inf 7 0 1 6 inf inf 0 |
0 10 3 4 2 0 5 6 7 7 0 1 6 16 9 0 |
0 10 3 4 2 0 5 6 7 7 0 1 6 16 9 0 |
+ |
2 |
0 inf 1 2 inf 0 inf 5 1 inf 0 4 2 5 4 0 |
0 7 1 2 7 0 8 5 1 8 0 3 2 5 3 0 |
0 7 1 2 7 0 8 5 1 8 0 3 2 5 3 0 |
+ |
3 |
0 7 9 inf inf 14 7 0 10 15 inf inf 9 10 0 11 inf 2 inf 15 11 0 6 inf inf inf inf 6 0 9 14 inf 2 inf 9 0 |
0 7 9 20 20 11 7 0 10 15 21 12 9 10 0 11 11 2 20 15 11 0 6 13 20 21 11 6 0 9 11 12 2 13 9 0 |
0 7 9 20 20 11 7 0 10 15 21 12 9 10 0 11 11 2 20 15 11 0 6 13 20 21 11 6 0 9 11 12 2 13 9 0 |
+ |
4
|
0 inf 3 inf -2 0 inf inf inf 7 0 -1 6 inf inf 0 |
0 10 3 2 -2 0 -1 0 5 7 0 -1 6 16 9 0 |
0 10 3 2 -2 0 -1 0 5 7 0 -1 6 16 9 0 |
+ |
5 |
0 inf -3 inf 2 0 inf inf inf 7 0 -1 -6 inf inf 0 |
В графе есть цикл отрицательного веса. |
В графе есть цикл отрицательного веса. |
+ |
Проанализировав оба протокола мы увидим, что обе программы работают корректно и выводят одно и тоже правильное решение.