4. Комбинаторный мгуа

Комбинаторный алгоритм МГУА (COMBI) во многом похож на многослойный итеративный МГУА. В частности, в обоих алгоритмах мы исходим из очень простых моделей (функциональных выражений для искомой зависимости), выбираем некоторые лучшие результаты и поэтапно усложняем их до получения модели оптимальной сложности. Отличие комбинаторного алгоритма от многослойного итеративного заключается прежде всего в гораздо более плавном переходе от моделей одного уровня к другим, более сложным. За счет такого более плавного перехода осуществляется более полный поиск среди возможных моделей-кандидатов, и, соответственно, возможно получение более адекватной модели. Недостатком такого подхода является необходимость расчета гораздо большего числа вариантов, вследствие чего этот алгоритм в первоначальном варианте был практически неработоспособен при числе переменных свыше примерно 30. В последние годы предложены способы эффективного уменьшения числа вариантов, расширяющие область применения этого алгоритма.

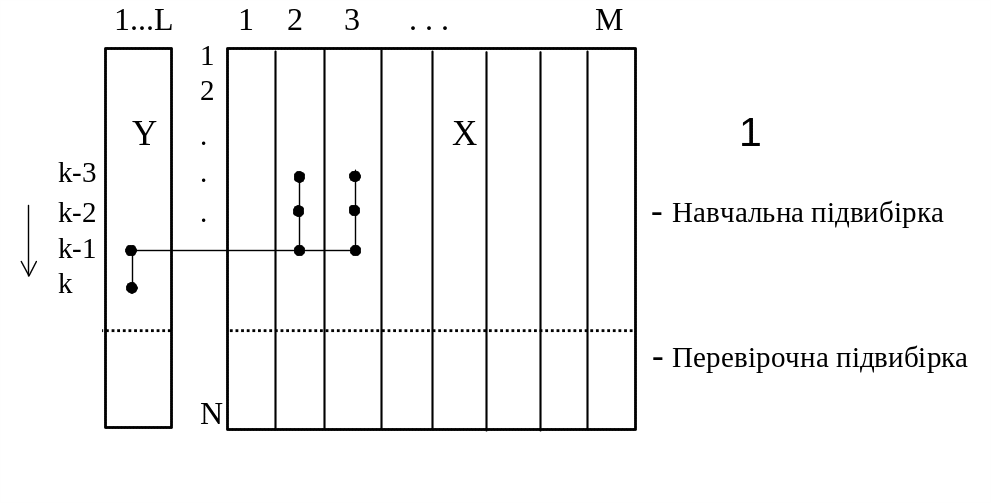
Блок-схема алгоритма приведена на рис.2. Входная выборка данных представляет собой таблицу, содержащую N точек наблюдений над М переменными. Выборка разделяется на две части. Примерно две трети точек относятся к обучающей подвыборке N_A, а оставшаяся одна треть используется как тестирующая подвыборка N_B. Разбиение первоначальных данных на подвыборки осуществляют таким образом, чтобы их вариации (дисперсии) были примерно равны.

Обучающая подвыборка используется для получения оценок коэффициентов полинома, а тестирующая подвыборка используется для выбора структуры оптимальной модели. Оптимальная модель определяется исходя из минимума некоторого внешнего критерия AR(s), такого, что:

Критерий требует выбора модели, которая будет иметь наиболее близкие значения критерия на обоих подвыборках. Для получения как можно более гладкой переборной функции (т.е., уменьшения шага различий между моделями), используемой для поиска модели оптимальной сложности (п.2), полный поиск производится на группах моделей одинаковой сложности. Например, вначале поиск оптимальной модели идет путем использования информации из отдельных столбцов выборки данных, таким образом, полный поиск на этом этапе ведется среди всех возможных моделей вида:

, .

На следующем этапе перебираются все модели вида:

,

Модели оцениваются по критерию и постепенно (путем последовательного введения по одной переменной) усложняются до тех пор, пока значения критерия уменьшаются.

Поскольку полный перебор всех вариантов очень ресурсоемок, был предложен метод уменьшения числа переменных после нескольких этапов вычислений. Такое уменьшение производится путем ранжирования переменных и выбора из них наиболее значимых - разновидность метода генетических алгоритмов.

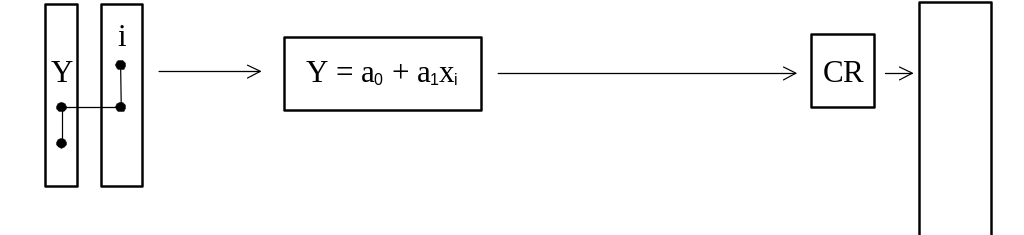
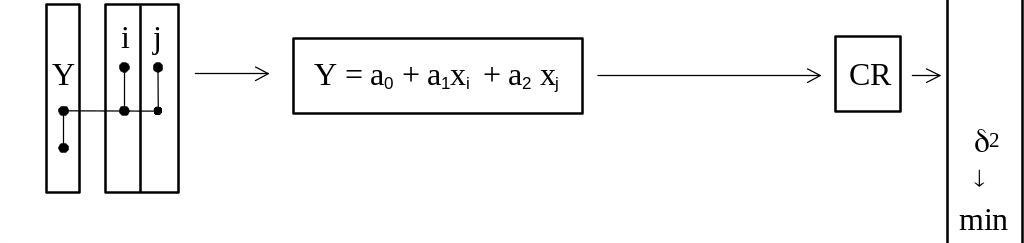Выходная

модель

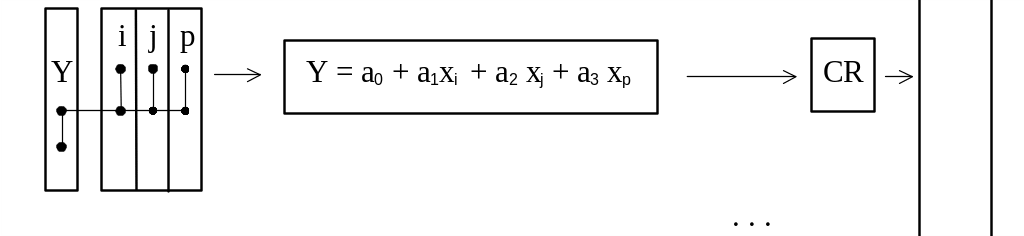
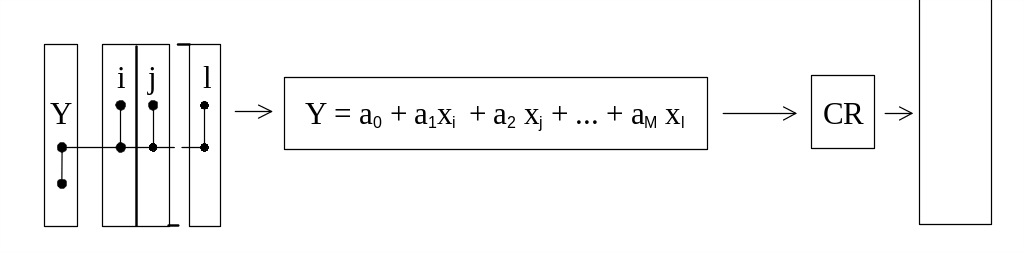
2 3 4 5

Рис.2. Блок-схема комбинаторного алгоритма МГУА

1. выборка данных;

2. ряды усложнения частичных описаний;

3. формы частичных описаний;

4. выбор оптимальных моделй;

5. дополнительное определение моделей по дискриминационному критерию