Оптимальное число слоев (уровней) обработки входной информации
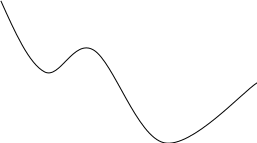
Для нахождения оптимального числа уровней обработки входной информации исходную последовательность данных разбивают на два блока (при небольшом числе данных эти блоки могут частично пересекаться), и один блок используют в качестве обучающей последовательности, другой – тестирующей. При этом в зависимости от числа уровней и качества входной информации мы можем получить следующие результаты (см. рис.15.1):
Ошибка
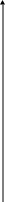
4
3
2
1
1 2 3 4
5 6 7
Количество уровней
Рис.15.1. Зависимость погрешности от числа уровней преобразования
И качества входных данных
данных недостаточно для построения адекватной модели;
очень большой уровень шумов;
единственная (нефизическая модель):
несколько возможных моделей (абсолютный минимум погрешности у физической модели).
Представленные на рис.15.1. зависимости погрешности для тестирующей последовательности соответствуют следующим случаям:
1 - кривая идет вниз без минимума – выборка не содержит достаточно эффективных для построения модели переменных;
2 - кривая идет вниз до некоторого предела и затем выполаживается – случай большого шума в переменных или неполных данных;
3 - наличие одного размытого (широкого) минимума – позволяет выбор уникальной нефизической (оптимальной с учетом шума) модели;
4 - зависимость содержит два и более минимумов – имеются несколько моделей, каждая из которых соответствует некоторому поднабору данных, либо моделям различной сложности.
Построение модели возможно только при наличии минимума на зависимости, т.е. для кривых 3-го и 4-го типов. Минимум погрешности определяет число слоев (уровней) в обрабатывающем алгоритме. Дальнейшее увеличение уровней не только приводит к переусложнению модели, но и снижает ее точность на реальных данных (для обучающей последовательности погрешность уменьшается).
Вообще говоря, метод МГУА приводит в общем случае к построению так называемых нефизических моделей, которые для их понимания еще нуждаются в интерпретации.
Физические и нефизические модели
Нефизическую модель можно сопоставить черному ящику, физическую – серому или белому. Но самое главное, что различает физическую модель от нефизической – это интерпретируемость. Физическую модель мы можем интерпретировать, т.е., мы можем отдельные элементы ее структуры увязать с некоторыми другими объектами, не входящими в данную модель, и таким образом выводить закономерности поведения данного элемента модели из поведения некоторых внешних объектов. Такой подход существенно расширяет диапазон объяснительной (предсказывающей) силы модели. Если меняются внешние условия, мы можем оценить применимость данной модели для новых условий и видоизменить модель, либо отдельные ее элементы.
В нефизической модели у нас нет внешней интерпретации, в силу чего при изменении внешних условий модель может стать неадекватной, но мы это определить будем (до определенного момента) не в состоянии. Не говоря уже о невозможности (или трудностях) управления, поскольку мы не знаем, что регулировать. Нужны некоторые передаточные звенья, связывающие модель с теми параметрами, которыми мы можем управлять – но такая связь – это уже интерпретация.
Вообще говоря, нет непроходимой стены между физическими и нефизическими моделями. Если мы некоторым вначале нефизическим параметрам модели сопоставим какие-то известные физические (и смысловые) величины, то мы переводим их в стадию частично интерпретируемых. В дальнейшем, по мере увеличения этих смысловых связей и объяснительной силы элементов данной модели она приобретает для нас характер физической модели. Например, к таким промежуточным параметрам относится индекс Джоу-Джонса – для специалистов он имеет статус физической модели, для неспециалистов – нефизической.
Таким образом, деление на физические и нефизические модели тесно связано с вопросами интерпретируемости, привычности и общепринятости.