1. Что называют множеством, элементом множества? Множеством называют совокупность объектов, объединенных по какому-нибудь общему признаку или свойству.  1. Объекты безразлично какой природы; 2. Общих признаком или свойств может быть несколько. Пример: 1)цифры десятичной системы счисления(0,1,2,3,4,..) 2)множество студентов и т.д. Элемент множества - это объекты из которых состоят множества.  Множества об означаются заглавными буквами латинского алфавита без индексов или с индексами.(А, В, С, ...). Элементы множества об означаются малыми буквами латинского алфавита. 2. Какие множества называются пустыми, конечными, бесконечными? Если элементы множества можно сосчитать, то множество является конечным. Если элементы сосчитать невозможно, то множество считается бесконечным.  Множество, не содержащее ни одного элемента, называется пустым. 3. Какие способы задания множеств Вам известны? Путём перечислением всех его элементов. Данный способ используют только для конечных множеств и то не всех. Пример: множество цветов светофора. А={красный, желтый, зеленый}. Замечания: при перечислении элементов множества порядок не важен; элементы указываются однократно; число элементов множества называется мощностью данного множества. Путём задания характеристических свойств. Характеристические свойства, это те свойства, которыми обладает любой элемент данного множества и не обладает ни один элемент не принадлежащий ему. Обозначение: Х={х/характеристич. свойства } = {х/х=Р(х)} Способ задания множеств с помощью числовой оси или прямоугольной системы координат. Решение с помощью кругов Эйлера. 4. Какие отношения между множествами Вы знаете?

Два множества A и B могут вступать друг с другом в различные отношения.         A включено в B, если каждый элемент множества A принадлежит также и множеству B:                     A равно B, если A и B включены друг в друга:                     A строго включено в B, если A включено в B, но не равно ему:            

Пересечения множеств.  Пересечением множеств А и В является множество С, элементами которого являются те элементы, которые одновременно принадлежат и множеству А, и множеству В. Обозначение: AB, где символ – знак пересечения двух множеств. Объединение множеств. Объединением множеств А и В является множество С, элементы множеств которого принадлежат хотя бы одну множеству А или В. Разность множеств. Разностью множеств А и В является множество С, элементы которого принадлежат множеству А, но не принадлежат множеству В(А без В; А\В) Дополнение множеств. Дополнениями множеств А является множество Ā(А с чертой), элементами которого являются элементы не принадлежащие А множеству. Декартово произведение. Декартово произведение множеств А и В является множество С, состоящее из элементов упорядоченных пар, первым объектом которых является элемент множества А, вторым - элемент множества В.(АкрестикВ) 5. Дайте определение объединения множеств. Приведите пример. Поясните с помощью диаграмм Эйлера. Объединение множеств - объединением множества А и В является множество С, элементы которого принадлежат хотя бы одному множеству А или В. например множество девушек группы 1421 и множество юношей 1421. Объединение- множество студентов группы 1421. Круги Эйлера оба заштрихованы. 6. Дайте определение пересечения множеств. Приведите пример. Поясните с помощью диаграмм Эйлера. Пересечения множеств. Пересечением множеств А и В является множество С, элементами которого являются те элементы, которые одновременно принадлежат и множеству А, и множеству В. Нарисовать два круга, и то место, где они пересеклись, заштриховать. 7. Дайте определение разности множеств. Приведите пример. Поясните с помощью диаграмм Эйлера. Разностью множеств А и В называется множество С, элементы которого принадлежат множеству А, но не принадлежат множеству В.  Круги либо вообще не пересекаются, либо заштрихован только один, и та часть, где они не пересекаются, тоже не заштрихована. 8. Дайте определение дополнения множества. Приведите пример. Поясните с помощью диаграммы Эйлера. Дополнениями множеств А является множество Ā(А с чертой), элементами которого являются элементы не принадлежащие А множеству. Либо на заштрихованной части пустой круг. 9. Как определяется Декартово произведение множеств? Декартово произведение множеств А и В является множество С, состоящее из элементов упорядоченных пар, первым объектом которых является элемент множества А, вторым - элемент множества В.(АкрестикВ)10. Что изучает комбинаторика? Комбинаторика изучает количество комбинаций, подчиненных определенным условиям, которые можно составить из элементов безразлично какой природы, заданного конечного множества. 11. Назовите типы комбинации, которые вам известны. Перестановки - это комбинации, состоящие из одних и тех же n-различных элементов и отличающихся только порядком их расположения. Обознач.: Pn Размещение - это комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. An(в степени m) Сочетание - это комбинации, составленные из n-различных элементов по m-элементов, отличающиеся друг от друга хотя бы одним элементом. Сn(в степени m) 12. Что называют перестановками? Перестановки - это комбинации, состоящие из одних и тех же n-различных элементов и отличающихся только порядком их расположения. Обознач.: Pn 13. По какой формуле вычисляют число перестановок из n различных элементов? Pn=n!(факториал), где n=1*2*3*4*5*...*n Пример: сколько различных 4-х значных чисел можно составить из цифр 1,2,3,4(использовать цифру 1 раз) Pn=1*2*3*4=24 14. Что называют размещениями? Запишите формулу, по которой вычисляют число размещений из n элементов по m. Размещение - это комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. An(в степени m) An(в степениm)=n!/(n-m)! Пример: сколько можно составить сигналов из 6-ти флажков разного цвета, взятых по два? А6(в степени 2)=6!/(6-2)!=6!/4!=5*6=30 15. Что называют сочетаниями? Запишите формулу, по которой вычисляют число сочетаний из n элементов по m. Сочетание - это комбинации, составленные из n-различных элементов по m-элементов, отличающиеся друг от друга хотя бы одним элементом. Сn(в степени m) СN(в степени m)=n!/m!*(n-m)! Пример: скользкими способами можно из 27-ми студентов выбрать 3-х дежурных? C27(в степ. 3) = 27!/3!*(27-3)!=27!/3!*24!=25*26*27/1*2*3 16. Для каких комбинаций важен порядок элементов? Перестановки. Объект А можно выбрать n-способами, объект В m-способами, объект С-k способами. Тогда тройку можно выбрать m*n*k способами. Тройка упорядоченная.  17. Для каких комбинаций важен состав элементов?Размещение и сочетание 18. Для каких комбинаций важен и порядок и состав элементов?Размещение 19. Для каких комбинаций важен только порядок элементов?Перестановки 20. Для каких комбинаций важен только состав элементов?Размещение  21. По какой формуле вычисляется число перестановок из n элементов, если элементы повторяются? Pn(с чертой)=n!/n1!*n2!*...*nk! 22. Какой формулой определяется число размещений с повторениями из n элементов по m элементов? Ān(в степени m)=n(в степени m) 23. Какой формулой определяется число сочетаний с повторениями из n элементов по m элементов? Ćn(в степ. M)=Cn+m-1(в степени m)

24. Какое событие называют случайным?Это событие, которое может либо произойти, либо нет. 25. Что называют испытанием? Все, что происходит вокруг нас - это испытание. Результат испытания - исход. Испытания проводятся честно. 26. Какое событие называют достоверным? Приведите примеры. Если при наличии определенных условий событие обязательно происходит, то оно называется достоверным.

Событие называют достоверным, если в данном испытании оно является единственно возможным его исходом.

27. Какое событие называют невозможным? Приведите примеры. Это событие, которое никогда не происходит. Невозможным, если в данном испытании оно является заведомо не может произойти.

28. Какие события называют совместными? Приведите пример. Это любое событие, которое представляет собой одновременное возникновение любых двух (или более) других событий. При раскладывании колоды карт, например, "черная пятерка" будет совместным событием, так как состоит из всех карт, которые являются и черными и имеют пять символов. Два события называют совместимыми, если появление одного из них не исключает появления другого в одном и том же испытании.

Испытание - однократное бросание игральной кости. Событие А - появление четырех очков. Событие В - появление четного числа очков. События А и В совместимые.

29. Какие события называют несовместными? Приведите примеры. События являются несовместными, если нет оснований считать, что одно из них имеет больше возможностей для появления. Из ящика с деталями наудачу извлечена деталь. Появление стандартной детали исключает появление нестандартной детали. События «появилась стандартная деталь» и «появилась нестандартная деталь» — несовместные.

Два события называют несовместимыми, если появление одного из них исключает появление другого в одном и том же испытании.

Испытание - однократное бросание монеты. Событие А - выпадение герба, событие В - выпадение цифры. Эти события несовместимы, так как появление одного из них исключает появление другого.

30. Какие события называют равновозможными? Приведите примеры. Такие события называются равно возможными, если нет оснований считать, что одно из них имеет больше возможностей для появления. Например монетка, орел или решка

Равновозможными считают события, если нет оснований полагать, что одно событие является более возможным, чем другие.

31. Какие события называют противоположными? Приведите примеры. Противоположными называют два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через A, то другое принято обозначать Ā. Их сумма равна 1.

Два события А и В называются противоположными, если в данном испытании они несовместимы и одно из них обязательно происходит. Событие, противоположное событию А, обозначают через .

Испытание - бросание монеты. Событие А - выпадение герба, событие В - выпадение цифры. Эти события противоположны, так как исходами бросания могут быть лишь они, и появление одного из них исключает появление другого.

32. Что называют полной группой событий? Приведите примеры событий, образующих полную группу. События образуют полную группу, если в результате испытания наступает одно и только одно из них.Предположим, проводится подбрасывание монеты. В результате этого эксперимента обязательно произойдет одно из следующих событий: : монета упадет орлом; : монета упадет решкой; : монета упадет на ребро; Таким образом, система является полной группой событий.

Говорят, что совокупность событий образует полную группу событий для данного испытания, если его результатом обязательно становится хотя бы одно из них.

Примеры полных групп событий: выпадение герба и выпадение цифры при одном бросании монеты; попадание в цель и промах при одном выстреле; выпадение одного, двух, трех, четырех, пяти и шести очков при одном бросании игральной кости.

33. Какие исходы испытания называют элементарными? О.Случайным (стохастическим) экспериментом или испытанием называется осуществление какого-либо комплекса условий, который можно практически или мысленно воспроизвести сколь угодно большое число раз.

О. Явления, происходящие при реализации этого комплекса условий, то есть в результате случайного эксперимента, называются элементарными исходами. Считается, что при проведении случайного эксперимента реализуется только один из возможных элементарных исходов. 34. Какие элементарные исходы называют благоприятствующими данному событию? Те, которые подходят нам Событие А называют благоприятствующим событию В, если наступление события А влечет за собой наступление события В.

Пусть при бросании игральной кости события U₂, U₄,  и U₆ -появление соответственно двух, четырех и шести очков и А - событие, состоящее в появлении четного числа очков; события U₂, U₄ и U₆  благоприятствуют событию А.

35. Сформулируйте классическое определение вероятности. Вероятность события А определяется как отношение благоприятствующих появлений этого события исходов к общему числу всех равно возможных, не совместных, образующих полную группу исходов. 36. Укажите недостатки классического определения вероятности. Неприемлемость к испытаниям с бесконечным числом исходов, ввод геометрической вероятности к точке в область.

Классическое определение вероятности не является при­годным для изучения произвольных случайных событий. Так, оно неприемлемо, если результаты испытания не равновозможные. Например, при бросании неправильной игральной кости выпаде­ние ее различных граней не равновозможное.

37. Что понимается под статистическим определением вероятности? Отношение частотой наступления события А называют отношение числа исходов, в которых событие А наступило к общему числу исходов всех испытаний. W(A)=m/n 38. Чем отличаются классическое и статистическое определения вероятности? Статистическое вычисляется после испытания. Классическое определение вероятности: отношение числа благоприятных исходов ко всем; а статистическое - предел кол-ва наблюдаемых благоприятных исходов к общему кол-ву.

39. Что понимают под субъективной вероятностью события? Это численное выражение уверенности конкретного лица в том, что данное событие в действительности произойдет.  40. Что называют суммой двух событий? Сумма событий А и В , называемыми событиями А+В заключается в появлении или события А, или события В, или их одновременного появления. Суммой нескольких событий является событие, заключающееся в появлении хотя бы одного события. 41. Что называют произведением двух событий? Произведением событий А и В называется событием, состоящим в появлении этих событий и А, и В. 42. Чему равна вероятность суммы несовместных событий? Сформулируйте теорему. P(А1+А2+...+Аn)=P(А1)+Р(А2)+...+Р(Аn) Вероятность суммы несовместных событий равна сумме вероятностей этих несовместных событий 43. Чему равна сумма вероятностей событий, образующих полную группу? Сумма вероятностей, образующих полную группу событий всегда равна 1. 44. Сформулируйте теорему умножения вероятностей зависимых событий. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:  P (AB) = P (A)*PA(B) 45. Дайте определение условной вероятности. Условная вероятность — вероятность одного события при условии, что другое событие уже произошло. Если накладываются ограничения. 46. Дайте определение безусловной вероятности. Априорная или безусловная вероятность, связанная с некоторым событием A, представляет собой степень уверенности в том, что данное событие произошло, в отсутствии любой другой информации, связанной с этим событием.  Если при вычислении вероятности никаких ограничений не на кладывается, то это безусловная вероятность. 47. Два события независимы. Что это означает? Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т. е. если условная вероятность события В равна его безусловной вероятности: Р(A)=Pbc(A)=1 48. Чему равна вероятность произведения двух независимых событий? P(A*B*C)=P(A)*P(B)*P(C) 49. Какие события называются независимыми в совокупности? Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т. е. если условная вероятность события В равна его безусловной вероятности: 50. Сформулируйте теорему умножения вероятностей n событий, независимых в совокупности. вероятность их совмещения равна произведению вероятностей этих событий

Р(А1,А2,А3,…Аn)= Р(А1)*Р(А2)*….Р(Аn)

51. Как найти вероятность появления хотя бы одного из n независимых в совокупности событий? Теорема. Вероятность появления хотя бы одного из событий А1 , А2 , ..., Аn , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий

Р (A) = 1 — Р (А1) * Р(А2)…Р(Аn) ( А- с чертой)

52. Как найти вероятность появления хотя бы одного из n независимых событий, имеющих одинаковые вероятности?

53. Если события не являются независимыми в совокупности, как найти вероятность того, что хотя бы одно из них произойдет?

Р(А*В*С)= Р(А)*Ра(В)*Рав(С)

54. Сформулируйте теорему сложения вероятностей совместных событий.

Суммой 2-х совместных событий называют событие, состоящее в появлении либо события A, либо события B, либо обоих сразу.

 Теорема. Вероятность суммы 2-х совместных событий равна сумме вероятностей этих событий без учета их совместного появления. p(A+B)=p(A)+p(B)−p(AB) 

Доказательство:

A+B=AB+AB+AB (сумма несовместных пар)

Тогда p(A+B)=p(AB)+p(AB)+p(AB)

Событие A=AB+AB,

Событие B=AB+AB

p(A+B)=p(A)−p(AB)+p(B)−p(AB)+p(AB)=p(A)+p(B)−p(AB) 

 

Замечание: в этой теореме может существовать 2 различные ситуации.

p(A+B)=p(A)+p(B)−p(A)p(B),  где A и B - независимые;

p(A+B)=p(A)+p(B)−p(A)p(B∖A),  где A и B - зависимые;

 

Вероятность р(А + В) суммы событий А и В равна

                      Р (А + В ) = р (А) + р (В) – р (АВ).                                                    55. Что называют гипотезами?

Гипотеза - предположение или догадка; утверждение, не предполагающее доказательство, в отличие от аксиом, постулатов, не требующих доказательств. 

Статистическая гипотеза- это предположение о виде распределение или о величинах неизвестных параметров генеральной совокупности, которая может быть проверена на основании выборочных показателей.

H₁, H₂,...,H_n образуют полную группу событий. Такие события иногда называют гипотезами.

56. Запишите формулу полной вероятности для n гипотез.

Событие А наступит только после того как наступит одно из несовместных событийВ1, В2 и т.д., образующих полную группу.

Вероятность события А в этом случае определяетсяы по формуле

P(A)=P(B1)*Pb1(A)+P(B2)*Pb2(A)+…+P(Bn)*Pbn(A) 57. Запишите формулу Байеса (переоценки гипотезы).

,где

 — априорная вероятность гипотезы A (смысл такой терминологии см. ниже);

 — вероятность гипотезы A при наступлении события B (апостериорная вероятность);

 — вероятность наступления события B при истинности гипотезы A;

 — полная вероятность наступления события B.

58. Какими должны быть испытания, чтобы можно было применять формулу Бернулли? при независимых испытаниях. Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей — при достаточно большом количестве испытаний. 

При условии что вероятность события А в каждом испытании постоянна и равна p( p(Aс чертой)=1-p-q 59. Какой вид имеет эта формула?Pn(k) n-сколько раз сделал k- сколько раз событие наступило 60. В каком случае формулой Бернулли нельзя воспользоваться?

При больших n (больше или равно) 10. 61. Какое число называют наивероятнейшим? Как находится это число?

K0 – наивероятнейшее число, если вероятность того, что событие наступит в независимых n- испытаниях (каждое из которых вероятность появления события равно р) в этих испытаниях К01 превышает по крайней мере не меньше вероятности остальных возможных исходов испытания..

Из двойного неравенства: np-q меньше или ровно<Kо<больше np+q

Если число np-q – дробное то существует одно число Ко,если число np-q – целое, то существует два Ко, а именно Ко и Ко +1. Если чсило р – целое т о Ко= n*p 62. Как найти вероятность того, что в n независимых испытаниях событие А наступит: а) менее m раз; б) более m раз; в) не менее m раз; г) не более m раз?

63. Локальная теорема Лапласа. Если вероятность p появления события А в каждом испытании постоянна, то Pn(K) приближённо равна: Pn(K)~~(=)~~(1/корень из n*p*q)*f(x), где x=k-n*p/корень из npq Замечания: 1) при n>(больше или равно)10 используем эту теорему 2)х округляем до сотых 3) если х меньше 0, то пользуемся равенством f(-x)=f(x) 4) значение f(x) находим в соответствующей таблице 5) чем больше n, тем точнее результат 6) если х больше 5  64. Интегральная теорема Лапласа. Теорема. Пусть производится n независимых опытов, в каждом из которых вероятность наступления события А одна и та же и равна  . Пусть m - число появления события A в n опытах. Тогда для достаточно больших n случайная величина m имеет распределение, близкое к нормальному с параметрами a=M(m)=np, 

 - интегральная функция Лапласа.

65. Формула Пуассона. 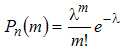,(3.4)

где  .

  66. Что называется случайной величиной? Случайная величина - это величина, когда в результате испытания примет одно и только одно возможное значение ,наперед неизвестное и зависящее от случайных причин, которые заранее учтены быть не могут. 67. Назовите виды случайных величин. Они бывают двух типов: дискретные и непрерывные. 68. Что понимается под дискретной случайной величиной? Дискретная случайная величина принимает отдельные изолированные возможные значения с определенными вероятностями.  69. Сколько возможных значений может у нее быть? Число возможных значений может быть и конечным, и бесконечным. 70. Что понимается под непрерывной случайной величиной? Непрерывная случайная величина может принимать все значения из некоторого конечного или бесконечного интервала. 71. Сколько возможных значений может у нее быть? Число возможных значений является бесконечным. 72. Какими способами можно задать дискретную случайную величину? Что бы задать дискретную случайную величину необходимо перечислить все его возможные значения и указать соответствующие им вероятности. Это можно сделать с помощью таблиц, графика, формулы. 73. Какие числовые характеристики случайной величины вам известны?

Числа, назначение которых в сжатом виде характеризовать основные особенности распределений случайных величин, называются числовыми характеристиками. Математическое ожидание и его свойства.

Математическим ожиданием (или средним значением) дискретной случайной величины называется сумма произведений всех её возможных значение на соответствующие им вероятности.

X			…
P			…

 

 

 

Дисперсия и среднее квадратическое отклонение.

Названные числовые характеристики дают представление о разбросе случайных величин относительно их среднего значения.

Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

Среднее квадратическое отклонение числа появления событий в n независимых опытах равно  .

Моменты распределения. Понятия математического ожидания и дисперсии являются частными случаями более общего понятия для числовых характеристик случайных величин – моментов распределения. Моменты распределения случайной величины вводятся как математические ожидания некоторых простейших функций от случайной величины. 

Мода дискретной случайной величины – это ее наиболее вероятное значение. Модой непрерывной случайной величиныназывается ее значение, при котором плотность  вероятности максимальна

Медиана случайной величины Х – это ее значение Ме , для которого имеет место равенство:   т.е. равновероятно, что случайная величина Х окажется меньше или больше Ме. Геометрически медиана – это абсцисса точки, в которой площадь под кривой распределения делится пополам (рис.  2). В случае симметричного модального распределения медиана, мода и математическое ожидание совпадают. 74. Дайте определение математического ожидания. Запишите формулы для вычисления математического ожидания дискретной случайной величины.

Математическим ожиданием (или средним значением) дискретной случайной величины называется сумма произведений всех её возможных значение на соответствующие им вероятности.

75. Дайте определение дисперсии. Запишите формулы для вычисления дисперсии дискретной случайной величины. Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

D = M( – M)². 76. Что такое среднее квадратическое отклонение случайной величины? Как оно вычисляется? в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания. Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин. 77. Какие законы распределения дискретной случайной величины вам известны?

Так как дискретная случайная величина имеет конечное или счётное множество значений, то их можно просто перечислить и указать соответствующие вероятности. Это можно сделать, например, в форме таблицы

Такую таблицу называют рядом распределения.

Примеры дискретных сл.вел: 1). Индикатор события I. Эта случайная величина имеет закон распределения : Если вероятность появления события   в некотором опыте равна p, то I принимает значение 1, если событие произошло, и значение 0, если событие не произошло. I можно назвать числом появлений события в одном опыте.

I	0	1
P	q	р

 

 

 

2). Биномиальный закон распределения. Случайная величина может принимать значения 0,1,2,…,n и каждому значению X=m соответствует вероятность  , где p+q=1. Этот закон распределения считается заданным, если известны числа n и p, через которые выражаются все вероятности. Случайную величину подчинённою этому закону   можно назвать числом появле­нии события в n независимых опытах.

З). Пуассоновский закон распределения. Случайная велbчина имеет возможные значения 0,1,2,3,…… и каждому значению Х=m со­ответствует вероятность  ,где   - некоторый параметр, вероятностный смысл которого будет указан несколько страниц спустя.

4). Гипергеометрический закон распределения. Возможные значения X: 0,1,…,n. И каждому значению X=m соответ­ствует вероятность P(X=m)=P = .  Эта случайная величина, например, равна числу m бракованных изделий среди n взятых наугад из партии объёма N, содержащей M бракованных изделий.

5). Геометрический закон распределения.

X	1	2	3	…	n	…
P	p	qp		…		…

  q=1-p

Если, например, p – вероятность изготовления бракованной детали, то случайная величина X с этим законом распределения будет равна общему числу деталей     до момента изготовления первой бра­кованной детали.

Построение ряда распределения удобно лишь для дискретных случайных величин, так как можно перечислить их все возможные значения

78. Что означает, что случайная величина распределена по биномиальному закону? Как определяются для этой величины? См вопрос 77 79. Что означает, что случайная величина распределена по закону Пуассона? Как найти математическое ожидание и дисперсию этой величины? См вопрос 77 80. Какие законы распределения непрерывной случайной величины вам известны?

Закон распределения непрерывной случайной величины нельзя задать также, как для дискретной. Он неприменим в силу того, что нельзя перечислить все бесконечное несчетное множество значений, а вероятности каждого отдельно взятого значения непрерывной случайной величины равны нулю.

1.Интегральная функция распределения..

Все по отдельности возможные значения непрерывных случайных величин перечислить нельзя - их бесконечно много. Поэтому естественно указывать вероятности не для отдельных значений, а для целых интервалов. Рассмотрим значения с.в.Х такие, что Х<х. Вероятность события X<х зависит от x, т.е. является функцией x. Эта функция и называется интегральной функцией распределения и обозначается через F(x). Итак, по определению 

                                      F(x)=P(X<x)

2 Дифференциальная функция распределения..

Дифференциальной функцией распределения или функцией плотности вероятности называется первая производная от интегральной функции распределения, т.е. F’(x)=f(x). Из этого определения видно, что функция плотности вероятности существует только для непрерывных случайных величин.