18.Суть метода вращения вокруг проец. Прямых. Определение углов наклона прямой общ. Положения к плск проекций этим методом.

С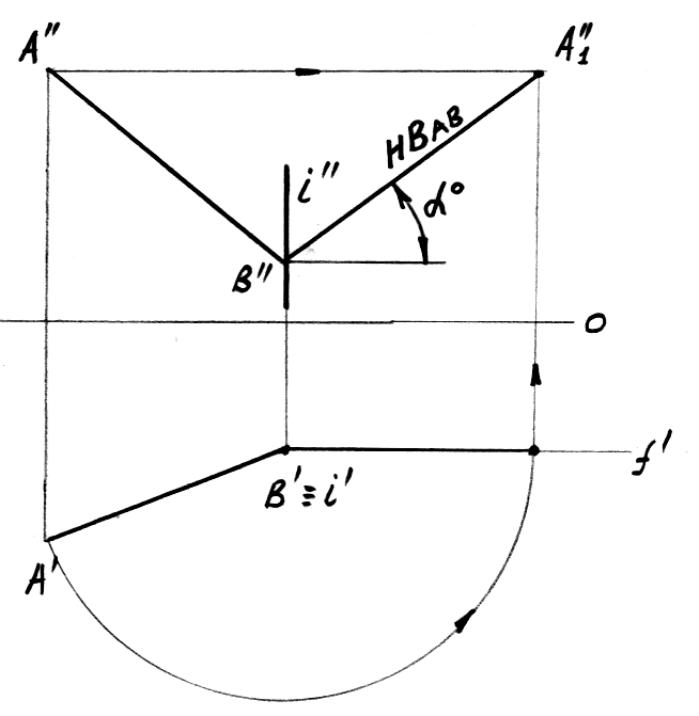 пособ состоит в том, что плск проекций остаются неизменными, а положение геометрических элементов изменяют путем вращения их вокруг оси, ⊥ 1ой из плск проекций т.о., чтобы они заняли частное положение относительно той или иной плск проекции, при которой задача будет решена или упроститься ее решение. При вращении точки вокруг оси, ⊥ 1ой из плск проекций, проекция точки на плск, к которым ⊥ ось вращения, перемещается по окружности, в то время, как др. проекция точки перемещается по прямой, II-ной соответствующим осям проекций.

НВ прямой и угол α^o определится, если прямую вращать вокруг горизонтально-проецирующей оси до параллельности плоскости проекций V. Ось проведем, например, через точку B

19.Суть метода плоскоIi перемещения. Решение 4 задач

Плск проекций остаются неподвижными, а геом. фигура перемещается до положения, когда задача будет решена или упростится ее решение. При плоскоII перемещении относительно 1ой из плск проекций, одна проекция траектории точки повторяет траекторию точки движения в пространстве, а др перемещается по прямой, II-ной оси х. проекция отрезка или плоской фигуры на плск проекций, II которой происходит перемещение, не меняет своего размера и формы, а меняет только положение.

4 задачи: 1)прямую сделать пр.уровня (1з); 2)плск сделать проецирующей(2з); 3) прямую сделать проецир. (2з); 4) плск сделать плск уровня (1з)

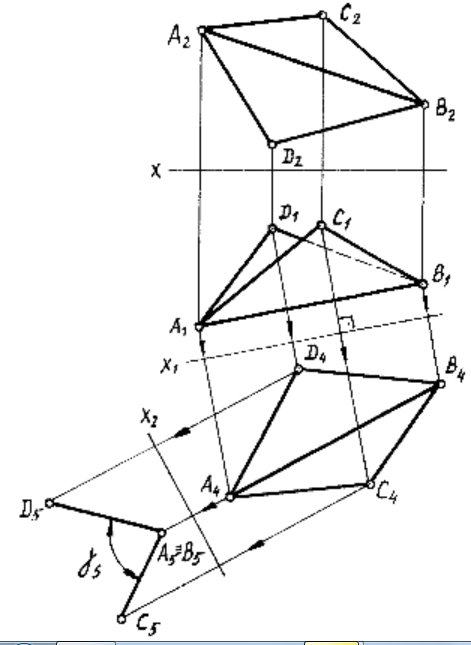
20.Метод замены плск проекций. Определить истинную величину двугранного угла

Сущность заключается в том, что предмет в пространстве остается неизменным, изменяется последовательно положения плск проекций, при этом всегда сохр-ся взаимная перпен-сть 2х пл-стей проекций. При перемещении пл-стей проекций расстояние от новой проекции т-ки до новой оси проекции равно расстоянию от заменяемой проекции т-ки до старой оси проекции.

21. Используя метод плоско || перемещения, определить расстояние между 2 || прямыми

22. Поверхности. Определитель пов-сти. Клас-ция пов-стей

Поверхность - непрерывная совокупность последовательных положений какой-либо линии, перемещающаяся в прост-ве по опред. закону или произвольно. Линия, образующая поверхность называется образующей. Образующей мб прямая или кривая линия, которая в процессе движения остается неизменной или деформируется. Неподвижные линии, по которым движется образующая называются направляющими (кинематич способ задания поверхности).

Определитель- сов-сть независимых усл-й однозначно задающих пов-сть в прост-ве и на чертежах. Различают две части определителя: геометрическую и алгометрическую. Геометрич часть определителя представляет собой набор постоянных геометр эл-тов (тчк, прямых, плск..), с помощью которых мб образована поверхность. Алгометр (описатель) часть содержит алгоритм формирования поверхности из геометр фигур, вкл в состав определителя.

Классификация: А)линейчатые: 1) развертывающиеся (линейчатые поверхности, которую можно без складок и разрывов развернуть на плоскость (совместить с плск): 1.1) цилиндрическая (образуется движением прямолинейн образующей || заданному направлению по некоторой криволинейной направляющей); 1.2) коническая (образована движением прямой (образующ), проходящ через неподвиж вершину, и скользящ по некоторой криволинейной направляющей); 1.3) поверхности с ребром возврата или тор (Образуется прямой, перемещающ в пространстве так, что она все время касается нек-ой пространств кривой, назыв-ой ребром возврата);

2)неразвертыв-ся: 2.1) поверх-ти с плск параллелилизма (пврх Каталана) [если прямая (образующ) движ по 2 направляющ, оставаясь ||ой в нек-ой плск, назыв плск параллелилизма, то получ-ся линейчатая пврх, назыв пврх с плск ||зма. Плск ||зма может выбираться произвольно. Для задания пврх этой плск на эпюре Монжа достаточно указать проекции направ-щих и проекции плск ||зма): 2.1.1)косая плск или гипербалический парабалоид (обе направл кривые/скрещ) 2.1.2) каноид (1 направл – кривая, др – прямая. Образующ || плск ||зма); 2.1.3)цилиндроид (обе направл – кривые).

Б) Нелинейчатые (кривые) пврх (образуются движ-ем в пространстве какой-либо кривой образующ, к-ая мб как плоской, так и пространств прямой постоянного или переменч вида): 1) пврх вращения (образ-ся вращением кривой или прямой линии вокруг оси вращения): сфера, тор,эллипсоид вращ-я, парабалоид вращ-я, однополосый гипербалоид вращ-я, двухполосный -||-;

2 )Каналовые пврх (образ-ся движ-ем сферы постоян или перемен r по нек-ым кривым направляющ); 3) пврх переноса (образ-ся перемещением нек-ой кривой образующ по нек-ой др прямой напрвляющей).

23. построить развертку пирамиды

24. построить развертку цилиндра

2 5. построить развертку конуса

2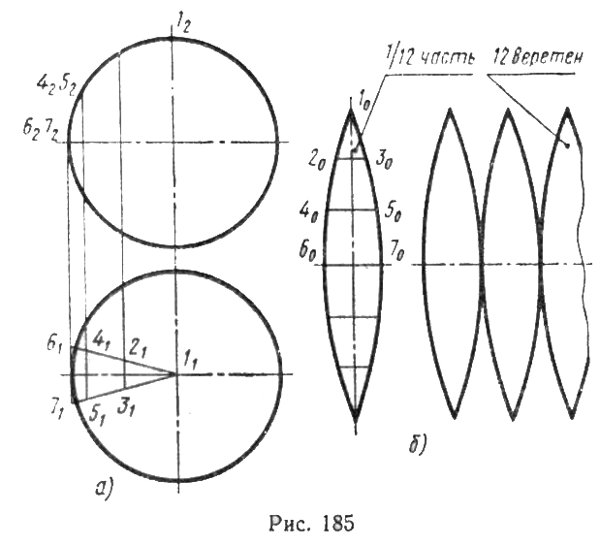 6. построить развертку сферы

27. теорема монжа о пересечении пврх второго порядка

Если в обе пов-сти 2ого порядка одновременно может быть вписана сфера определ.радиуса,то линии пересечения пов-стей распадается на плоские кривые.

28. вспомог эксцентрич сфер для построения линии пересеч пврх При построении линии пересечения поверхности вращения с циклической поверхностью, несущей на себе каркас окружностей, либо двух поверхностей вращения, оси которых не пересекаются, но поверхности имеют общую плоскость симметрии, параллельную плоскости проекции в качестве вспомогательных поверхностей можно брать сферы, центры которых не совпадают, то есть эксцентрические сферы.   Построение следует выполнить на той плоскости проекций, к-ой || плск симметрии и где проекции окружностей – отрезки прямых, по следующему алгоритму: 1) Отметить точки пересечения главных меридианов, очерков проекций поверхностей. 2) В области пересечения поверхностей взять на 1ой пврх (торе, кольце, циклич пврх, эллиптич цилиндре или эллиптич конусе) окружность. 3) Из центра этой окружности к ее плск провести перпендикуляр до пересеч с осью вращения другой пврх. Это центр вспомог сферы. 4) Определить R вспомог сферы. Его длина = расстоянию от центра сферы до точек выбранной окружности. 5) Провести вспомог сферу и найти окружности, по к-ым сфера пересекает др пврх. 6) Найти точки пересеч этих окружностей с выбранной вначале (построение повторить с п.2).

  Методом эксцентрических сфер строят одну проекцию линии пересеч, а 2ую находят по принадлежности линии пересечения одной из исходных пврх.

Способ применяется при следующих условиях:

1) Пересекающиеся поверхности должны содержать в себе систему окружностей. 2)Плоскость симметрии пересекающихся поверхностей является общей 3) Плоскость симметрии пересекающихся поверхностей параллельна какой-либо плоскости проекций.