8. Задание плоскости на эпюре.
Плоскость на Эпюре задается проекциями элемента, определяющими плоскость в пространстве, а именно:
А) проекциями трех точек, не лежащих на одной прямой;
Б) проекциями прямой и точки, не лежащей на этой прямой;
В) проекциями двух параллельных прямых;
Г) проекциями двух пересекающихся прямых;
Д) отсеком (плоскость, ограниченная линией)
Е) следами (Следами называются линии пересечения плоскости с плоскостями прекции. Чтобы построить следы плоскости нужно построить следы двух прямых, принадлежащих плоскости)
9. Главные линии плоскости
Из всех прямых необходимо выделить особо расположенные, имеющие важное значения как вспомогательные элементы при различных графических операциях:
Горизонталь плоскости – это прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекции
Фронталь плоскости – это прямая, лежащая в плоскости и параллельная фронтальной плоскости проекции.
Профиль плоскости – это прямая, лежащая в плоскости и параллельная П3.
1 0. Теорема о линии наибольшего наклона плоскости к плоскостям проекции.
Линия наибольшего наклона к плоскости (л. н. н.) - это прямая, лежащая в плоскости и образующая с плоскостью проекции наибольший угол. Она служит для измерения угла наклона плоскости, в которой она лежит, с соответствующей плоскостью проекции.
С точки зрения геометрии, линии, лежащие в плоскости и перпендикулярные линиям уровням плоскости.
Т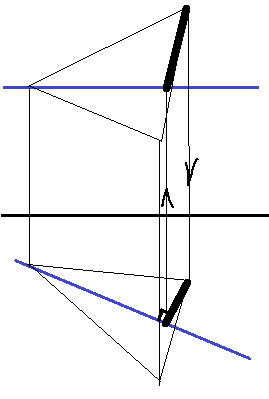
еорема
1. Горизонтальная проекция л н н к П1 ⊥
горизонтальной проекции горизонтали
плоскости.
H принадлеж АВС (h2||Ox → h1)
C1O1⊥→ h1 – C2O2
Теорема 2.Фронтальная проекция л н н ⊥ фронтальной проекции фронтали плоскости.
11. Плоскости частного положения.
Плоскости уровня – это плоскости || одной из плоскостей проекции и ⊥ двум другим.
1. горизонтальная плоскость – это плоскость || П1
2. фронтальная плоскость – это плоскость || П2
3. профильная плоскость – это плоскость || П3.
12. Проецирующие плоскости. Основные свойства проецирующих плоскостей. Пример.
Проецирующие плоскости – это плоскости ⊥ одной из плоскостей проекции.
1. горизонтально проецирующая плоскость – это плоскость ⊥ П1
На горизонталь плоскости проекция горизонтально проецирующей плоскости проецируется в прямую (след), расположенную под углом к оси Ох. Фронтальный след П2 - оси х. Характерным для горизонтально проецирующей плоскости является то, что горизонтальная проекция любого геометрического элемента, лежащего в плоскости, всегда располагаются на горизонтальном следе плоскости.
2.фронтально проецирующая плоскость – это плоскость ⊥ фронтальной плоскости проекции.
3.профильно проецирующая плоскость – это плоскость ⊥ П3.
Основное свойство проецирующих плоскостей: одна проекция фигуры, принадлежащая проецирующей плоскости проецируется в отрезок прямой, совпадающий с одним следом плоскости (проецирующ).
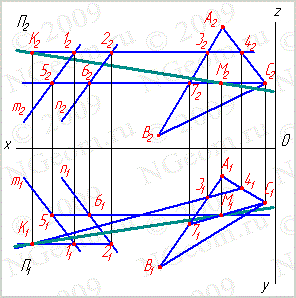
13. Алгоритм построения линии пересечения плоскостей.
Для построения линии пересечения двух плоскостей пересекают их последовательно двумя вспомогательными плоскостями. Получаем две точки, общие этим плоскостям. Соединяя их, получаем линию пересечения двух плоскостей. В качестве вспомогательных плоскостей используем проецирующую плоскость или плоскость уровня.
1
4.
Пересечение прямой с плоскостью. Алгоритм
построения.
1. Заключаем прямую во вспомогательную плоскость (проецирующую)
2. Находим линию пересечения двух плоскостей (заданной и проецирующей)
3. Там, где прямая пересекла линию сечения получаем точку пересечения прямой с плоскостью.
4. Определяем видимость.
15. Перпендикулярность прямой и плоскости. Определение расстояния до плоскости. Пример. Определения расстояния до прямой.
П
рямая
перпендикулярна плоскости, если она
перпендикулярна двум пересекающимся
прямым этой плоскости.
16. Взаимно перпендикулярные плоскости.
Если плоскость проходит через перпендикуляр к другой плоскости, то она перпендикулярна этой плоскости
17. Суть метода замены плоскостей. 4 основных задачи преобразования чертежа
Сущность метода замены плоскостей проекции заключается в том, что предмет в пространстве остается неизменным. Изменяются последовательно положения плоскостей проекции. При этом всегда сохраняется взаимная перпендикулярность двух плоскостей проекции. Замену производят до тех пор, пока задача не будет решена или не упростится ее решение.
При перемене плоскостей проекции расстояние от новой проекции точки до новой оси проекции равно расстоянию от заменяемой проекции точки до старой оси проекции.
Четыре основные задачи.
Прямую сделать прямой уровня (1 замена)
Прямую сделать проецирующей (2замены)
Плоскость сделать проецирующей (1 замена)
Плоскость сделать плоскостью уровня (2 замены)