- •Предмет начертательной геометрии
- •Система Монжа. Ортогональные проекции точки на 2 и 3 плоскости
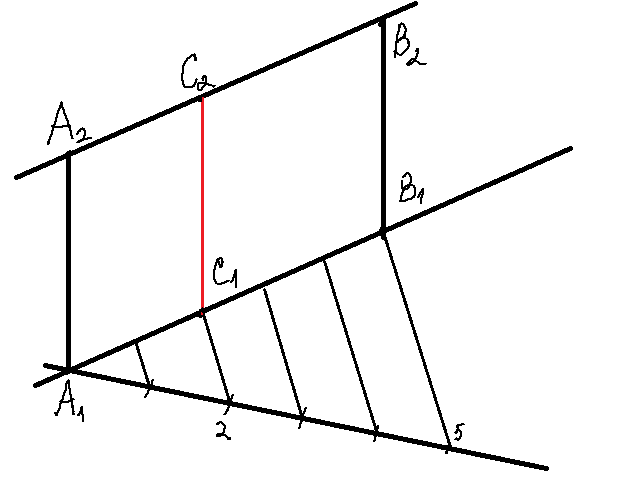
- •3.Деление отрезка в данном отношении.
- •4.Определение углов наклона прямой к плоскостям проекций. Пример
- •5.Прямые частного положения
- •6. Взаимное положение прямых в пространстве. Определение видимости (метод конкурирующих точек).
- •7 . Теорема о проецировании прямого угла. Определение расстояния от точки до прямой частного положения.
- •8. Задание плоскости на эпюре.
- •9. Главные линии плоскости
- •1 0. Теорема о линии наибольшего наклона плоскости к плоскостям проекции.
- •11. Плоскости частного положения.
- •12. Проецирующие плоскости. Основные свойства проецирующих плоскостей. Пример.
- •18.Суть метода вращения вокруг проец. Прямых. Определение углов наклона прямой общ. Положения к плск проекций этим методом.
- •19.Суть метода плоскоIi перемещения. Решение 4 задач
- •20.Метод замены плск проекций. Определить истинную величину двугранного угла
- •21. Используя метод плоско || перемещения, определить расстояние между 2 || прямыми
- •22. Поверхности. Определитель пов-сти. Клас-ция пов-стей
- •29. Использование вспомогат.Концентрических сфер для построения линии перес-ния пов-стей
- •31. Аксонометрические проекции. Определение. Схема построения аксонометрических изображений. Коэффициенты искажения
- •32. Построить в аксонометрии (по заданным ортогональным проекциям) точки пересечения прямой общего положения с цилиндром
- •33. Построение линии пересечения 2х пов-стей. Схема.
Предмет начертательной геометрии
Начертательная геометрия рассматривает различные методы изображения пространственных фигур на плоскости и графические способы решения задач, относящие к этим фигурам по плоским изображениям. Умение читать и составлять чертежи – одна из важных сторон квалификации инженера любой специальности.
М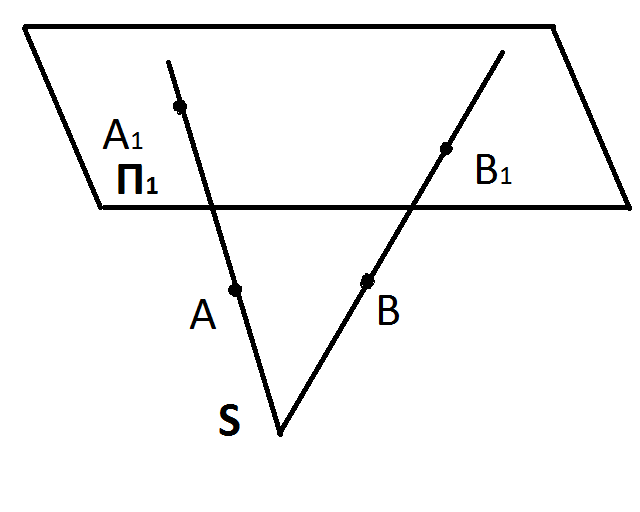 етод
проецирования
етод
проецирования
Метод проецирования состоит в том, что через точки, данные в пространстве, и подлежащие изображению на какой-либо поверхности проводят прямые (проецирующие лучи) и находят точки пересечения этих прямых с заданной поверхностью. Полученные точки называют проекциями данных точек на заданной поверхности.
Аппарат проецирования состоит из плоскости проекции (П1), на которой получаются проекции, и проецирующих прямых (SA, SB)
Виды проецирования
Существует два основных вида проецирования: центральное (коническое) и параллельное (цилиндрическое)
Если проецирующие лучи проходят через одну точку, называемую центром проекции (S), то этот вид проецирования называется центральным или коническим.
Изображение, полученное с помощью центрального проецирования, обладает наилучшей наглядностью, но наихудшей измеримостью.
Если центром проекции будет бесконечно удаленная точка, а проецируемые прямые будут параллельны, то этот вид проецирования называется параллельным или цилиндрическим.
Параллельное проецирование подразделяется на ортогональное (прямоугольное), если проецирующие прямые перпендикулярны к плоскости проекции, и косоугольные, если проецирующие прямые не перпендикулярны к плоскости проекции.
Система Монжа. Ортогональные проекции точки на 2 и 3 плоскости
О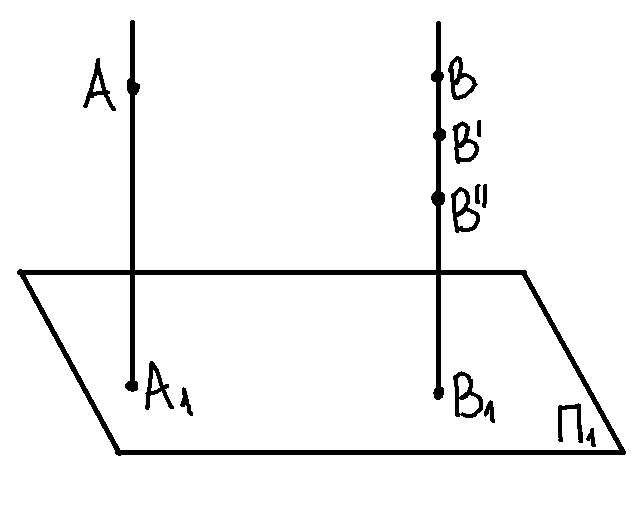
 ртогональной
проекцией точки на плоскость является
основание перпендикуляра, опущенного
из данной точки на плоскость.
ртогональной
проекцией точки на плоскость является
основание перпендикуляра, опущенного
из данной точки на плоскость.
Одна проекция точки не определяет положение точки в пространстве, нужны дополнительные данные. Например, проекция на другую плоскость.
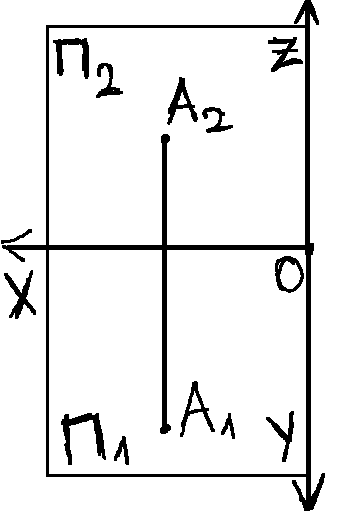
Метод ортогональной проекции (метод Монжа) основан на том, что геометрическую фигуру проецируют ортогонально на две взаимно перпендикулярные плоскости П1 и П2.
Плоскость П2 совмещаем с плоскостью П1 поворотом вокруг оси х. Получается плоский чертеж, где будут выполняться все построения. Этот чертеж называется комплексным чертежом или эпюром.
Э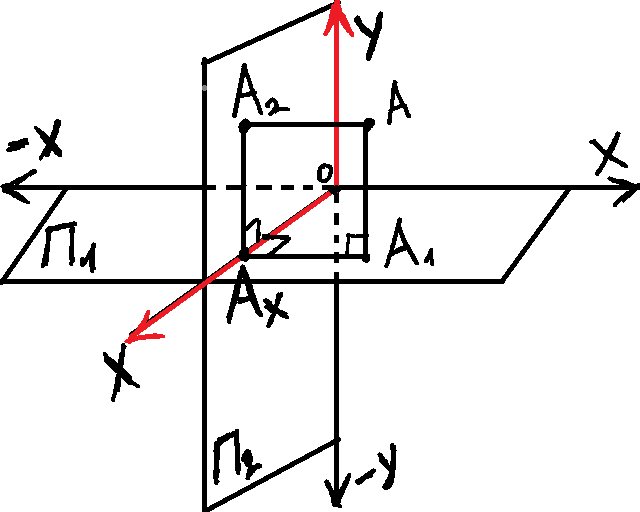 пюром
называется чертеж, на котором плоскости
ортогональных поверхностей соединены
с одной из них.
пюром
называется чертеж, на котором плоскости
ортогональных поверхностей соединены
с одной из них.
Основное св-во проекции точек: 2 проекции точек лежат на одном перпендикуляре к оси проекции.
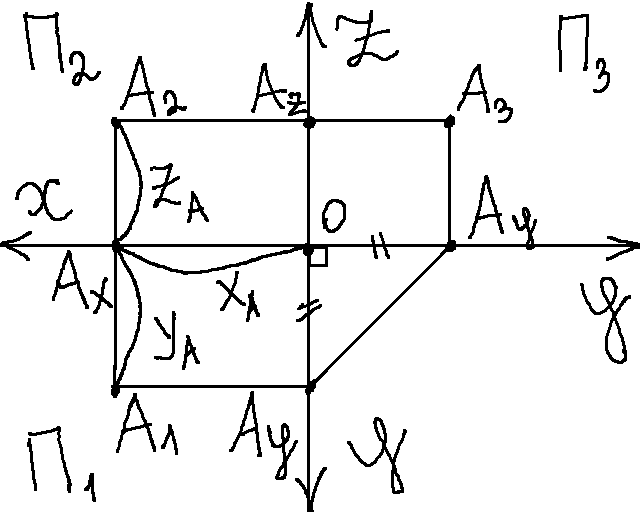
Ортогональная система 3 плоскостей проекции:
П1 - горизонтальная плоскость проекции
П2 - фронтальная плоскость проекции
П3 - профильная плоскость проекции
А1 - горизонтальная проекция точки А
А2 - фронтальная проекция точки А
А3 - профильная проекция точки А
3.Деление отрезка в данном отношении.
Е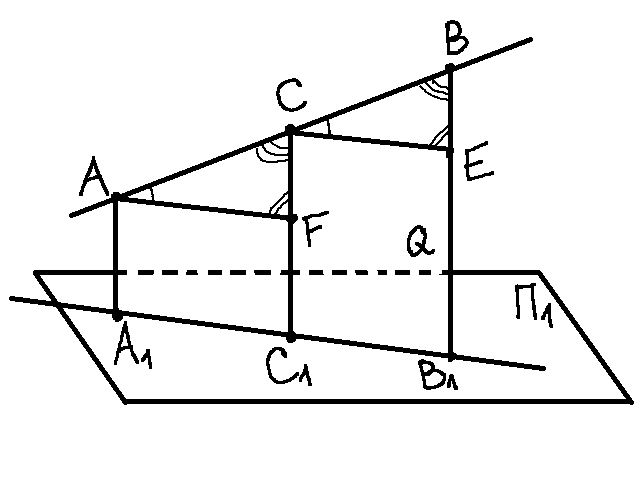 сли
точка делит отрезок прямой в данном
отношении, то проекции этой точки делят
одноименные проекции прямой в том же
отношении.
сли
точка делит отрезок прямой в данном
отношении, то проекции этой точки делят
одноименные проекции прямой в том же
отношении.
С принадлежит АВ, СС1 принадлежит Q,
AF || А1С1; СЕ||С1В1, ∆ACF ≈ ∆CBE (по 3 углам), АС/А1В1 = СВ/С1В1:
Разделить отрезок АС/СВ=2/3: