2. Проектирование стропильных конструкций.

сегментная раскосная ферма

Результаты статического расчета сегментной раскосной фермы марки 2ФС18 для III снегового района, приведенными в табл. 3.

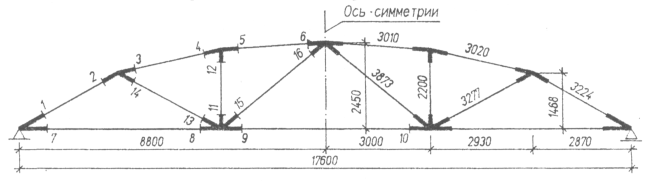
Рис.6. Схема расположения сечений сегментной раскосной фермы.

Для анализа напряженного состояния элементов фермы построим эпюры усилий N и М от суммарного действия постоянной и снеговой нагрузки (снеговая I), как показано на рис.7.

Рис.7. Эпюры усилий N и M в сегментной раскосной фермы.

Таблица 3. Усилия от постоянной и снеговых нагрузок.

№ сече-ния	постоянная			Постоянная + снеговая 1			Постоянная + снеговая 2			Постоянная + снеговая 3			Постоянная + снеговая 4
	N	M	Q	N	M	Q	N	M	Q	N	M	Q	N	M	Q
1	-808,678	0,6422	2,223	-1144,59	0,90896	3,1464	-1044,66	0,80636	2,96172	-948,481	0,66272	2,79756	-916,264	0,6422	2,736
2	-808,678	4,7424	2,223	-1144,59	6,71232	3,1464	-1044,66	6,2814	2,96172	-948,481	5,82996	2,79756	-916,264	5,68632	2,736
3	-801,268	4,0508	-0,988	-1134,102	5,73344	-1,3984	-1009,96	5,34356	-1,2958	-918,950	4,9742	-1,2958	-878,977	4,85108	-1,27528
4	-801,268	1,4326	-0,988	-1134,102	2,02768	-1,3984	-1009,96	1,92508	-1,2958	-918,950	1,5352	-1,2958	-878,977	1,47364	-1,27528
5	-780,52	1,1856	0,4446	-1104,736	1,67808	0,62928	-983,545	1,94484	0,32148	-895,042	1,3908	0,42408	-855,993	1,43184	0,36252
6	-780,52	2,3218	0,4446	-1104,736	3,28624	0,62928	-983,545	2,77324	0,32148	-895,042	2,44492	0,42408	-855,993	2,36284	0,36252
7	719,5604	2,1242	0,1976	1018,455	3,00656	0,27968	929,3364	2,86292	0,23864	843,768	2,69876	0,15656	815,1015	2,65772	0,13604
8	719,5604	3,0134	0,1976	1018,455	4,26512	0,27968	929,3364	3,9368	0,23864	843,768	3,38276	0,15656	815,1015	3,30068	0,13604
9	788,671	2,0748	0	1116,273	2,93664	0	950,6148	3,08028	-0,2052	894,3900	2,34156	0	841,5305	2,44416	-0,08208
10	788,671	2,0748	0	1116,273	2,93664	0	950,6148	1,93116	-0,2052	894,3900	2,34156	0	841,5305	1,99272	-0,08208
11	-20,254	-0,3952	0,247	-28,6672	-0,5594	0,3496	-48,2433	-0,19	-0,01976	-22,0392	-0,33364	0,1444	-28,4004	-0,21052	0,00076
12	-20,254	-0,0988	0,247	-28,6672	-0,1398	0,3496	-48,2433	0,18848	-0,01976	-22,0392	-0,24244	0,1444	-28,4004	-0,34504	0,00076
13	65,1092	0	0,2964	92,15456	0	0,41952	57,02432	0	0,399	53,9258	-0,04104	0,37848	42,59876	-0,04104	0,37848
14	65,1092	0,8892	0,2964	92,15456	1,25856	0,41952	57,02432	1,197	0,399	53,9258	0,684	0,37848	42,59876	1,05336	0,21432
15	-14,079	0,494	-0,0988	-19,9272	0,6992	-0,13984	35,66148	0,5966	-0,0988	-3,18288	0,3914	-0,11932	14,79264	0,53504	-0,0988
16	-14,079	0,1976	-0,0988	-19,9272	0,27968	-0,13984	35,66148	0,34124	-0,0988	-3,18288	0,1976	-0,11932	14,79264	0,23864	-0,0988

Нормативные и расчетные характеристики тяжелого бетона класса В50, твердеющего в условиях тепловой обработки при атмосферном давлении, эксплуатируемого в окружающей среде влажностью 60% (γ_b2 = 0,9): R_bn = R_b,ser = 36 МПа; R_b = 0,9*27,5 = 24,75 МПа; R_btn = R_bt,ser = 2,3 МПа; R_bt = 0,9*1,55 = 1,395 МПа; R_bp = 35 МПа (см. табл.2.3 [4]); Е_b = 35000 МПа.

Расчетные характеристики ненапрягаемой арматуры: продоль­ной класса A-III, R_s = R_sc = 365 МПа; E_s = 200 000 МПа; поперечной класса A-I, R_sw = 175 МПа; Е_я = 210 000 МПа.

Нормативные и расчетные характеристики напрягаемой арма­туры класса А-VI: R_sn = R_s,ser = 980 МПа; R_s = 815 МПа; E_s= 190 000 МПа.

Назначаем величину предварительного напряжения арматуры в нижнем поясе фермы σ_sp = 900 МПа. Способ натяжения арматуры — механический на упоры. Проверяем условие (1) [2] при отклонении значения предварительного напряжения р = 0,05 σ_sp = 0,05*900 =45 МПа.

Так как σ_sp+р = 900 + 45 = 945 МПа < R_s,ser = 980 МПа и σ_sp — р = 900 — 45 = 855 МПа > 0,З R_s,ser = 294 МПа, то условие (1) выполняется.

Расчет элементов нижнего пояса фермы. Согласно эпюрам усилий N и М, наиболее неблагоприятное сочетание усилий имеем в сечении номер 9(10) при N = 1116,275 кН и М = 2,94 кН•м. Поскольку в предель­ном состоянии влияние изгибающего момента будет погашено неупру­гими деформациями арматуры, то расчет прочности выполняем для случая центрального растяжения (рис. 2.18, а). Требуемую площадь сечения растянутой напрягаемой арматуры находим по формуле (137) [5]:A_s,tot = N/(ηR_s) = 1116,275*10³(1,1*945) = 1073,9 мм².

Принимаем 8 Ø14 А-VI (А_s,tot = 1231 мм² или A_sp=A`_sp = 615,5 мм²).

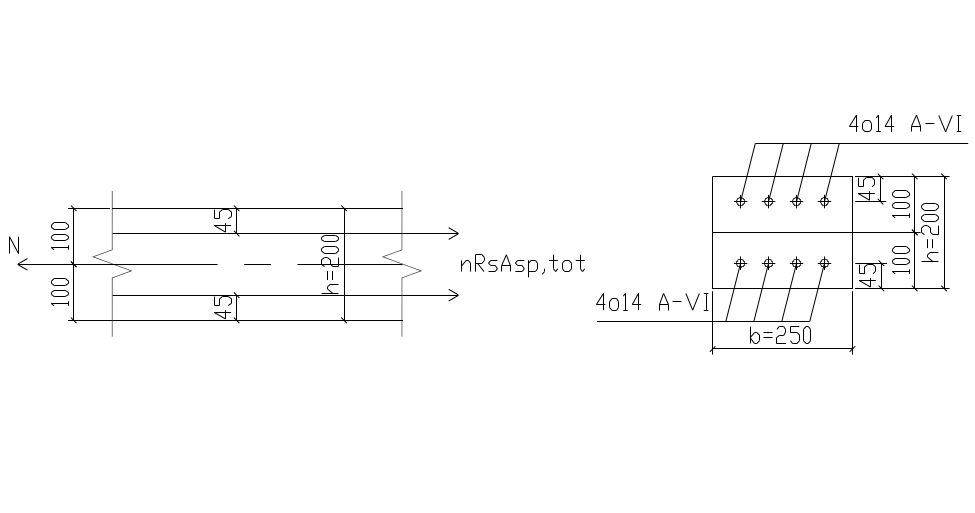
Рис.8. К расчету сечений нижнего пояса сегментной раскосной фермы.

Расчет трещиностойкости нижнего пояса фермы выполняем на действие усилий от нормативных нагрузок, величины которых получим путем деления значений усилий от расчетных нагрузок на средний коэффициент надежности по нагрузке γ_fm = 1,213 (см. рис. 2.16). Для сечения 12 получим:

усилия от суммарного действия постоянной и полного значения снеговой нагрузки N = N/ γ_fm = 1116,275/1,213 = 920,3 кН,

М = М/ γ_fm = 2,94/1,213 = 2,43 кН*м;

усилия от постоянной и длительной части снеговой нагрузки

N_l = [N_g + (N – N_g)k_l]/γ_fm = [788,671 + (1116,275 – 788,671)*0,5]/ 1,213 = 785,22 кН,

М_l = [M_g + (М – M_g)k_l]/ γ_fm = [2,1 + (2,94 – 2,1)0,5]/1,213 = 2,08 кН*м,

где k_l = 0,5 — коэффициент, учитывающий долю длительной составляющей снеговой нагрузки согласно п. 1.7 [3].

По табл. 1, б [5] находим, что нижний пояс фермы должен удовлетворять 3-й категории требований по трещиностойкости, т. е. допускается непродолжительное раскрытие трещин шириной 0,3 мм и продолжительное шириной 0,2 мм.

Геометрические характеристики приведенного сечения вычис­ляем по формулам (11) — (13) [5] и (168) — (175) [6].

Площадь приведенного сечения A _red = А + αA_sp,tot = 250*200 + 5,143*1231 = 56331 мм², где α = E_s/E_b = 190000/35000 = 5,429.

Момент инерции приведенного сечения I_red = I + αА_sрy²_sр + αA'_spy'_sp²= 250*200³/12 + 5,429*615,5*65² + 5,429*615,5*65² = + 1,95*10⁸ мм⁴, где y_sp = y`_sp = h/2 — а_р = 200/2 — 45 = 65 мм.

Момент сопротивления приведенного сечения W^inf_red = I_red/y₀ = 1,95* 10⁸/100 = 1,95*10⁶ мм³, где y₀ = h/2 = 200/2 = 100 мм.

Упругопластический момент сопротивления по наиболее растянутой грани в стадии эксплуатации W^inf_pl = γW^inf_red = 1,75*1,95*10⁶ = 3,413•10⁶ мм³, где γ = 1,75 принимается по табл. 38 [6].

Определим первые потери предварительного напряжения арма­туры по поз. 1 — 6 табл. 5 [2] для механического способа натяжения арматуры на упоры.

Потери от релаксации напряжений в арматуре

σ₁ = (0,22σ_sp/R_s,ser - 0,1)σ_sp = (0,22*900/980 - 0,1)900 = 92 МПа.

Потери от температурного перепада σ₂ = 1Δt = 1*65 = 65 МПа.

Потери от деформации анкеров, расположенных у натяжных устройств σ₃ = Δl/l)E_s = (3,35/19000)190000 = 33,5 МПа, где Δl = 1,25 + 0,15d = 1,25 + 0,15*14 = 3,35 мм и l = 18+ 1 = 19 м = 19000 мм.

Потери σ₄ и σ₅ равны нулю.

Напряжения в арматуре с учетом потерь по поз. 1 — 5 и соответ­ственно усилие обжатия будут равны: σ_sp1 = σ_sp — σ₁ — σ₂ — σ₃ = 900 - 92 - 65 – 33,5 = 709,5 МПа; P_I = σ_spIA_{sp ш} = 709,5*1231 = 783,4*10³ Н = 873,4 кН.

Определим потери от быстронатекающей ползучести бетона:

σ_bp=P_I/A_red= 873,4*10³/56331 = 15,5 МПа;  = 0,25 + 0,025R_bp = 0,25 + 0,025*35 = 1,125>0,8, принимаем = 0,8; поскольку σ_bp/R_bp =15,5/35 = 0,443 < , то σ₆ = 0,85*40σ_bp/R_bp= 0,85*40*0,443 = 15,1 МПа.

Таким образом, первые потери и соответствующие напряжения в напрягаемой арматуре будут равны: σ_losl = σ_l + σ₂ + σ₃ + σ₆ = 92 + 65 + 33,5 + 15,1 = 205,6 МПа; σ_spl = σ_sp - σ_losl = 900 — 205,6 = 694,4 МПа.

Усилие обжатия с учетом первых потерь и соответствующие напряжения в бетоне составят: P₁ = σ_sp1A_sp,tot = 694,4 • 1231 = 854,8*10³Н = 854,8 кН; σ_bp = P₁/A_red = 854,8*10³/56331 = 15,2 МПа. Поскольку σ_bp/R_bp = 15,2/35= 0,434 < 0,95, то требования табл. 7 [2] удовлетворяются.

Определим вторые потери предварительного напряжения арма­туры по поз. 8 и 9 табл. 5 [2].

Потери от усадки бетона σ₈ = 40 МПа.

Потери от ползучести бетона при σ_bp/R_bp = 0,434 < 0,75 будут равны σ₉ = 150*0,85σ_bp/R_bp = 150*0,85*0,434 = 55,3 МПа.

Таким образом, вторые потери составят σ_los2 = σ₈ + σ₉ = 40 + 55,3 = 95,3 МПа, а полные будут равны σ_los = σ_losl + σ_hs2 = 205,6 + 95,3 = 301,1 Мпа > 100 МПа.

Вычислим напряжения в напрягаемой арматуре с учетом полных потерь и соответствующее усилие обжатия: σ_sp2 = σ_sp — σ_los = 900 — 301,1 = 598,9 МПа; Р₂ = σ_sp2A_sp,tot = 598,9* 1231 = 737,2*10³Н = 737,2 кН.

Проверку образования трещин выполняем по формулам п. 4.5 [2] для выяснения необходимости расчета по ширине раскрытия трещин.

Определим расстояние r от центра тяжести приведенного сечения до ядровой точки, наиболее удаленной от максимально растянутой внешней нагрузкой грани сечения. Поскольку N = 920,3 кН > P₂ = 737,2 кН, то величину r вычисляем по формуле r = W^inf_pl/[A + 2(A_sp + A`_sp)] = 3,413*10⁶/[250*200 + 2*5,429(615,5+ +615,5)] = 53,9 мм.

Тогда М_rp=Р₂(е_ор2+r) = 737,2*10³(0 + 53,9)= 39,7*10⁶ Н*мм = 39,7 кН*м; соответственно М_crc = R_bt,serW^inf_pl + М_rp = 2,3 • 3,419•10⁶ + 39,7*10⁶ = 47,5*10⁶ Н*мм = 47,5 кН*м.

Момент внешней продольной силы M_r = N(e₀ + r) = 920,3*10³(2,64 + 53,9)= 52,03•10⁶ Н*мм = 52,03 кН*м, где е₀ = M/N = 2,43*10⁶/(920,3*10³) = 2,64 мм.

Поскольку М_сгс = 47,5 кН•м < М_г = 52,03 кН*м, то трещины, нормальные к продольной оси элемента, образуются, и требуется расчет по раскрытию трещин.

Расчет по раскрытию трещин выполняем в соответствии с тре­бованиями пп. 4.14 и 4.15 [2]. Определим величину равнодействую­щей N_tot и ее эксцентриситет относительно центра тяжести приведен­ного сечения: N_tot = N—Р₂= 920,3—737,2 = 183,1 кН; e_0,tot = M/N_tot = 2,43*10⁶/(183,1*10³) = 13,4 мм.

Поскольку e_0,tot = 13,4 мм < 0,8h₀ = 0,8*155 = 124 мм, то при­ращения напряжений в арматуре S_p вычисляем по формуле (148) [2]:

от действия полной нагрузки

σ_s = [N(z_s - e_s) – P₂(z_s - e_sp)]/(A_spz_s) = [920,3*10³(110 – 52,36) — 737,2*10³(110 — 55)]/(615,5*110) = 184,63 МПа,

где e_s = y₀ — а_р — e₀ = 100 — 45 — 2,64 = 52,36 мм;

e_sp = y₀ — а_р = 100 — 45 = 55 мм; z_s = h₀ — а`_р = 155 — 45 = 110мм;

от действия длительной нагрузки

σ_s = [785,22*10³(110—52,36)—737,2•10³(110—55)]/(615,5*110) = 69,63 МПа.

Вычислим ширину раскрытия трещин от непродолжительного действия полной нагрузки по формуле (144) [2]:

а_сгс = _l(σ_s/E_s)20(3,5 - 100)³d = 1,2*1*1(184,63/190000)20(3,5-100*0,02)³l4 = 0,265 мм,

где  = 1,2; _l = 1,0;  = 1 (для арматуры класса А-VI);  = A_sp/(bh₀) = 615,5/(250*113,4) = 0,022 > 0,02, принимаем μ=0,02, здесь h₀ = h/2 + e_0,tot= 100 + 13,4 = 113,4 мм (см. п. 4.15 [6]); d = 14 мм — диаметр арматуры.

То же, от непродолжительного действия длительных нагрузок

а_сгс = 1,2*1*1(69,63/190000)20(3,5 — 100*0,02)³l4 = 0,111 мм.

То же, от продолжительного действия длительных нагрузок (для тяжелого бетона j_l = 1,6 — 15m = 1,6 — 15*0,02 = 1,3 = 1,3):

а_сгс= 1,2*1,3*1(69,63/190000)20(3,5- 100*0,02) ³l4 = 0,144 мм.

Таким образом, ширина непродолжительного раскрытия трещин от действия длительных и кратковременных нагрузок будет равна a_crc1 = 0,265 — 0,111 + 0,144 = 0,298 мм<[0,3 мм], а ширина про­должительного раскрытия трещин в нижнем поясе фермы составит а_сгс = 0,144 мм<[0,2 мм].

Расчет элементов верхнего пояса фермы. В соответствии с эпюрами усилий N и М (см. рис. 2.17), наиболее опасным в верхнем поясе фермы будет сечение 2 с максимальным значением продольной силы. Размеры сечения и расположение продольной арматуры дано на рис. 2.19, а.

Для сечения 2 имеем усилия от расчетных нагрузок: N = 1144,59 кН; М = 6,71 кН*м; N_l = 808,68 кН; М₁ = 4,74 кН•м. Находим: рас­четную длину элемента (см. табл. 33 [2] l₀ = 0,9l = 0,9•3,224 = 2,902 м; расчетный эксцентриситет е₀ = M/N = 6,71•10⁶/(1144,59*10³) = 5,86 мм; случайный эксцентриситет е_a  h/30 = 180/30 = 6мм, е_а  l/600 = 3224/600 = 5,4мм, е_а  6мм, принимаем e_a = 6мм.

Поскольку l₀=2,71м < 20h = 20*0,18 = 3,6 м, e₀=5,86 мм < е_а = 6мм, то расчет прочности верхнего пояса фермы выполняем по методике расчета сжатых эле­ментов на действие продольной силы со случайным эксцентрисите­том согласно п.3.64 [7].

Принимая в первом приближении j = 0,8 вычислим требуемую площадь сечения продольной арматуры по формуле

Принимаем 418 A-III, (A_s,tot = 1018 мм²).

При N_l= 808,68/1144,59 = 0,707, l₀/h = 2902/180 = 16,1 и а` = 30 мм ≥ 0,15h = 27 мм по табл. 26 и 27 [7] находим j_b = 0,796 и j_sb = 0,794. Так как _s = R_sA_s,tot/(R_bA) = 365*1018 / (24,75*250*180) = 0,334, то j = j_b + 2*(j_sb- j_b)_s=0,796+2(0,794 - 0,796)0,334=0,795  0,8 то уточнять расчет не требуется.

Рис. 9. К расчету прочности сечений элементов сегментной раскосной фермы

а — для верхнего пояса; б — для стоек и раскосов

Так же удовлетворяются требования по минимальному конст­руктивному армированию, поскольку m % = (A_s,tot/A)100% = [1018/(250*180)]100= 2,26% > 0,2 % (при l₀/h<10).

Поперечную арматуру конструируем в соответствии с требовани­ями п. 5.22 [2] из арматуры класса Вр-I диаметром 5 мм, устанавли­ваемую с шагом s = 350 мм, что менее 20d = 20•18 = 360 мм и менее 500 мм.

Расчет элементов решетки. К элементам решетки относятся стой­ки и раскосы фермы, имеющие все одинаковые размеры поперечного сечения b = 150, h = 120 мм для фермы марки 2ФС18 (рис. 9, б).

Максимальные усилия для подбора арматуры в элементах решет­ки определяются из таблицы результатов статического расчета фер­мы с учетом четырех возможных схем нагружения снеговой нагруз­кой.

Раскос 13-14, подвергающийся растяжению с максимальным усилием N= 92,154 кН. Продольная ненапрягаемая арматура по индивидуальному заданию класса A-III, R_s = R_sc = 365 МПа. Требу­емая площадь сечения рабочей арматуры по условию прочности составит A_s = N/R_S = 92,154*10³/365 = 252,5 мм². Принимаем 4  10A-III, (А_s=314мм²).

Стойка 11-12, подвергающийся сжатию с максимальными усилиями N= 28,67 кН и N_l= 20,25 кН. Расчетная длина l₀ = 0,8l = 0,8*2,45 = 1,96 м. Так как l₀/h = 1,96/0,12 = 16,33 < 20, то расчет выполняем без учета влияния прогиба на значение эксцентри­ситета продольной силы. Поскольку e_ah/30 = 120/30 = 4 мм;

e_al/600 = 2450/600 = 4,1 мм; e_a  5 мм, принимаем e₀ = е_а = 5 мм.

Вычислим требуемую площадь сечения продольной арматуры по формуле

Принимаем 410 A-III, (A_s,tot = 314 мм²).

Аналогично конструктивно армируем остальные сжатые эле­менты решетки, так как усилия в них меньше, чем в стойке 11-12.

Расчет и конструирование опорного узла фермы.

Усилие в нижнем поясе в крайней панели N = 1018,46 кН, а опорная реакция Q = Q_max = 600,3 кН.

Необходимую длину зоны передачи напряжений для продольной рабочей арматуры  14 мм класса А-IV находим по требованиям п. 2.29 [2]:

l_p = (_p_sp/R_bp + _p)d = (0,25•815/35 + 10)14 = 222 мм, где _sp = 815 МПа (большее из значений R_s и _spl) а _p = 0,25 и _p =10 (см. табл. 28 [2]).

Выполняем расчет на заанкеривание продольной арматуры при разрушении по возможному наклонному сечению ABC, состоящему из участка АВ с наклоном под углом 45° к горизонтали и участка ВС с наклоном под углом 27,6° к горизонтали (см. приложение VIII).

Координаты точки В по рис. 2.20 будут равны: у = 102 мм, х = 300 + 102 = 402 мм.

Ряды напрягаемой арматуры, считая снизу, пересекают линию ABC при у, равном: для 1-го ряда — 30 мм, l_Х = 300 + 30 = 330 мм; для 2-го ряда — 170 мм (пересечение с линией ВС), l_х = 535 мм. Соответст­венно значения коэффициента _sp = l_x/l_p (см. табл. 24 [2]) для рядов напрягаемой арматуры составят: для 1-го ряда — 360/222 = 1,486; для 2-го ряда — 535/222 = 2,41.

Усилие, воспринимаемое напрягаемой арматурой в сечении ABC: N_sp = R_s_spiA_spi = 815(1,486*615,5 + 2,41*615,5) = 1954,36*10³Н = 1954,36 кН.

Из формулы (1) [8] находим усилие, которое должно быть восп­ринято ненапрягаемой арматурой при вертикальных поперечных стержнях:

N_s = N— N_sp = 1018,46 – 1954,36 = - 935,9 кН.

Требуемое количество продольной ненапрягаемой арматуры за­данного класса A-III (R_s = 365 МПа) будет равно A_s,min = 0,15N/ R_s = 0,15*1018,46*10³/365 = 418,5мм². Принимаем 6  10 A-III, A_s = 471 мм².

Ненапрягаемую арматуру располагаем в два ряда по высоте: 1-й ряд — у = 70 мм, пересечение с линией АВ при х = 370 мм, 1_Х = 370 — 20 = 350 мм; 2-й ряд — у = 130 мм, пересечение с линией ВС, при х = 457 мм, 1_Х = 457 — 20 = 437 мм.

В соответствии с п. 5.14 [2] определяем требуемую длину анкеровки ненапрягаемой продольной арматуры в сжатом от опорной реакции бетоне. По табл. 37 [2] находим: _аn = 0,5; _аn = 8; _аn = 12; l_аn,min = 200 мм.

По формуле (186) [2] получим: 1_аn = (_аnR_s/R_b + _an)d = (0,5*365/15,3+8)10 = 199,3мм > _and = 12*10 = 120 мм и < l_an,min = 200 мм. Принимаем 1_аn = 200 мм. Тогда значение коэффици­ента условий работы ненапрягаемой арматуры _s5 = l_x/l_an при l_x > l_аn будет равно _s5 = 1.

Следовательно, усилие, воспринимаемое ненапрягаемой продольной ар­матурой, составит: N_S = R_S_s5tA_st = 365 (1*235,5 + 1*235,5 ) = 171,9*10 ³Н = 171,9 кН> 935,9 кН, т. е. принятое количество ненапрягаемой арматуры достаточно для выполнения условия прочности на заанкеривание.

Выполняем расчет опорного узла на действие изгибающего мо­мента, исходя из возможности разрушения по наклонному сечению АВ₁C₁ (см. рис. 10). В этом случае, при вертикальных хомутах должно удовлетворяться условие (2) [10]:

Qz_QN_spz_sp + N_sz₅ + q_swc²/2,

где q_sw = R_swA_sw/s — усилие в хомутах на единицу длины.

Высоту сжатой зоны бетона определим по формуле х = (N_sp + N_s)/(bR_b) способом последовательных приближений, уточняя значения N_sp и N_s по положению линии АВ₁C₁ на каждой итерации.

В первом приближении вычислим высоту сжатой зоны при N_sp и N_s из предыдущего расчета: х = (1954,36 – 935,9)10³/(250*24,75) = 164,6мм. Точка В₁ будет иметь координаты: x = 585 мм, у = 285 мм.

Так как все ряды напрягаемой и ненапрягаемой арматуры пересека­ются снова с линией АВ₁, то значение высоты сжатой зоны составит х = 164,6 мм при N_sp = 1954,36 кН и N_S = -935,9 кН. Тогда z_sp = z_s = 780 — 100 — 164,6/2 = 597,7 мм.

Поперечная арматура устанавливается конструктивно. Принимаем вертикальные хомуты минимального диаметра 6 мм класса A-I с рекомендуемым шагом s = 100 мм.

Определяем минимальное количество продольной ар­матуры у верхней грани опорного узла в соответствии с п. 6.2 [8]: A_s = 0,00bh= 0,0005*250*780= 98мм². Принима­ем 2  8 A-III, A_s= 101мм².

Рис. 10. К расчету опорного узла фермы

Рис. 1. в – Схема расположения связей

Рис.1. б -Продольный разрез одноэтажного

однопролетного промышленного здания