Вычисление значений элементарных функций. Вычисление значений алгебраического многочлена (метод Горнера).

Общепринятый сейчас способ вычисления многочленов восходит к Ньютону и называется схемой Горнера. Эта универсальная (то есть применимая к любому многочлену) схема предельно проста и изящна. Она получается из формулы (1) вынесением за скобки x всюду, где это возможно:

 f (x) = xⁿ + a₁x^n–1 + a₂x^n–2 + ... + a_n–1x + a_n (1)

f (x) = (...(((x + a1)·x + a2)·x + a3)...)·x + an.

(2)

Порядок действии при вычислении  f (x) определяется скобками в (2): сначала сложение внутри самой внутренней пары скобок (его результат обозначим через p₁), затем умножение и сложение внутри следующей пары скобок (результат p₂) и т.д.:

ì  p1 = x + a1; ï  p2 = p1x + a2; í  p3 = p2x + a3; ï  · · · · · · · · · · · · · · · · · · î  pn = pn–1x + an,     f (x) = pn;

(3)

всего n–1 умножений и n сложений ².

Вычисление значений аналитических функций и степенные ряды.

Функция f называется аналитической в точке x₀, если в некоторой окрестности этой точки она разлагается в степенной ряд:

Степенным рядом называется ряд вида: c₀ + c₁x + c₂x² + c₃x³ + ...    

где c₀, c₁, c₂, ... - постоянные числа, называемые коэффициентами ряда.

Ряд Тейлора:

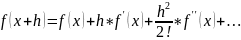
Численное решение алгебраических и трансцен-дентных уравнений.

Трансцендентное уравнение — уравнение, не являющееся алгебраическим. Обычно это уравнения, содержащие показательные, логарифмические, тригонометрические, обратные тригонометрические функции.

Численное решение уравнений - нахождение приближённых решений алгебраических и трансцендентных уравнений.

Численное решение алгебраических уравнений разбивается на следующие этапы:

1. выделение кратных корней, сводящее задачу к решению уравнения с простыми корнями;

2. определение границ, между которыми могут лежать корни уравнения;

3. разделение корней, т. е. указание промежутков, каждый из которых содержит не более одного простого корня;

4. грубое определение приближённого значения корня, выполняемое графически или каким-либо иным способом (например, при помощи изучения перемен знака левой части уравнения);

5. вычисление корня с заданной точностью.

Отделение корней.

Если функция F(x), определяющая уравнение F(x)=0, на концах отрезка [a;b] принимает значения разных знаков, т.е. F(a)*F(b)<0 (3), то на этом отрезке содержится, по крайней мере, один корень уравнения.

Как табулирование.

Оценки корней алгебраических уравнений.

Вычисление точности найденного корня

Основные методы уточнения корней уравнения (дихотомии, хорд, касательных, простой итерации).

Метод хорд. На выбранном отрезке проводим прямую соединяющую две крайнее точки(хорду), в точке пересечения x₀ проводим перпендикуляр к графику функции (при следующем шаге крайняя точка смещается к перпендикуляру), ответом будет ответом будет x при длине перпендикуляра равной нашей точности.

Метод касательных:

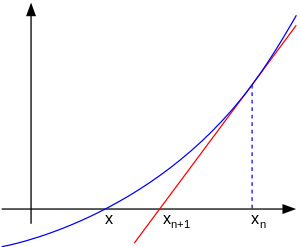
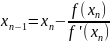
X_n –крайняя точка

F’(x_n) – производная от функции, при x=x_n

Идем от последней точки, до тех пор пока разница между текущей точкой и предыдущей не станет меньше погрешности