1. ДЕЙСТВИЯ НАД ПРИБЛИЖЕННЫМИ ВЕЛИЧИНАМИ.

   1. Абсолютная и относительная погрешность.

   2. Верные цифры.

   3. Погрешности элементарных операций.

   4. Прямая и обратная задачи теории погрешностей.

2. ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ.

   1. Вычисление значений алгебраического многочлена (метод Горнера).

   2. Вычисление значений аналитических функций и степенные ряды.

3. ЧИСЛЕННОЕ РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕН-ДЕНТНЫХ УРАВНЕНИЙ.

   1. Отделение корней.

   2. Оценки корней алгебраических уравнений.

   3. Основные методы уточнения корней уравнения (дихотомии, хорд, касательных, простой итерации).

   4. Решение систем нелинейных уравнений.

4. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕ-СКИХ УРАВНЕНИЙ.

   1. Метод Гаусса (схема полного исключения, сведение к треугольной матрице, проблема погрешности, схема главных элементов).

   2. Разложение матрицы в произведение треугольных и метод Краута.

   3. Метод квадратных корней.

   4. Метод простой итерации и сходимость итераций.

   5. Метод Зейделя.

   6. Метод прогонки для систем с трех-диагональной матрицей.

   7. Краткая характеристика других методов.

5. ПРОБЛЕМА СОБСТВЕННЫХ ЗНАЧЕНИЙ И МЕТОДЫ ЕЕ РЕШЕНИЯ.

   1. Поиск максимального по модулю собственного числа и соответствующего собственного вектора (степенной метод, метод скалярных произведений).

6. АППРОКСИМАЦИЯ ФУНКЦИЙ.

   1. Среднеквадратическая аппроксимация и метод наименьших квадратов.

   2. Среднеквадратическая аппроксимация функций на интервале.

   3. Аппроксимация алгебраическими многочленами.

   4. Аппроксимация ортогональными многочленами.

   5. Равномерная аппроксимация функций (понятие).

   6. Интерполяция функций.

   7. Интерполяционный многочлен Лагранжа.

   8. Конечные разности.

   9. Интерполяционные формулы.

   10. Интерполирование функций двух переменных.

   11. Численное дифференцирование.

   12. Интерполирование сплайнами.

7. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ.

   1. Квадратурные формулы Ньютона-Котеса, Чебышева, Гаусса.

   2. Вычисление несобственных интегралов. Кубатурные формулы.

   3. Вычисление кратных интегралов.

   4. Метод Монте-Карло.

8. ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ.

   1. Задача Коши: постановка и пути решение.

   2. Простейшие методы решения задачи Коши.

   3. Методы Рунге-Кутта.

   4. Решение задачи Коши для систем уравнений.

   5. Краевые задачи.

   6. Разностные методы.

   7. Метод прогонки.

Действия над приближенными величинами

Измерить или вычислить какую-либо величину абсолютно точно не всегда возможно. Поэтому в вычислительной практике преимущественно имеют дело не с точными значениями величин, а с их приближенными значениями.

Под приближенным значением величины понимают значение, незначительно отличающееся от точного значения и заменяющее последнее в вычислениях. При решении практических задач приходится не только приближенно находить значения величин, входящих в данную формулу и производить над ними указанные в формуле действия, но и оценивать возможные погрешности, допущенные как при определении числовых значений отдельных величин, так и при подсчете окончательного результата.

Абсолютная и относительная погрешность.

Абсолютной погрешностью или, короче, погрешностью приближённого числа называется разность между этим числом и его точным значением (при этом из большего числа вычитается меньшее).

Пример 1. При округлении 1284 до 1300 абсолютная погрешность составляет 1300 – 1284 = 16.  При округлении  до 1280 абсолютная погрешность составляет 1284 – 1280 = 4.

Относительной погрешностью приближённого числа называется отношение абсолютной погрешности приближённого числа к самому этому числу.

 Пример 2. В школе 197 учащихся. Округляем это число до 200.  Абсолютная погрешность составляет 200–197=3. Относительная погрешность равна 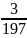 или округлённо,  .

То есть, если известно точное значение числа, то относительной погрешностью приближённого числа называется отношение абсолютной погрешности приближённого числа к точному числу. Но в большинстве случаев невозможно узнать точное значение приближённого числа, а значит, и точную величину погрешности. Однако всегда можно установить, что погрешность (абсолютная или относительная) не превосходит некоторого числа.

Пример 3. Продавец взвешивает арбуз на чашечных весах. В наборе гирь наименьшая – 50 г. Взвешивание дало 3600 г. Это число – приближённое. Точный вес арбуза неизвестен. Но абсолютная погрешность не превышает 50 г. Относительная погрешность не превосходит  .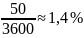

Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей), называется предельной абсолютной погрешностью. Число, заведомо превышающее относительную погрешность (или в худшем случае равное ей), называется предельной относительной погрешностью. 

В примере 3 за предельную абсолютную погрешность можно взять 50 г, а за предельную относительную погрешность  – 1,4 %.

Величина предельной погрешности не является вполне определённой. Так, в примере 3 можно принять за предельную абсолютную погрешность 100 г, 150 г и вообще всякое число большее, чем 50 г. На практике берётся по возможности меньшее значение предельной погрешности. В тех случаях, когда известна точная величина погрешности, эта величина служит одновременно предельной погрешностью.

Для каждого приближённого числа должна быть известна его предельная погрешность (абсолютная или относительная). Когда она прямо не указана, подразумевается, что предельная абсолютная погрешность составляет половину единицы последнего выписанного разряда. Так, если приведено приближённое число 4,78 без указания предельной погрешности, то подразумевается, что предельная абсолютная погрешность составляет 0,005. Вследствие этого соглашения всегда можно обойтись без указания предельной погрешности числа, округлённого по выше рассмотренным правилам.

Предельная абсолютная погрешность обозначается греческой буквой   («дельта»); предельная относительная погрешность – греческой буквой   («дельта малая»). Если приближённое число обозначить буквой, то  .