[Ред.]Математика

Твір Аль Хорезмі про арифметику зіграв надзвичайно важливу роль в історії математики. І хоча його справжній арабський текст загублений, зміст відомий у латинському перекладі 12 ст., єдиний рукопис якого зберігається в Кембріджі. У цьому творі вперше даний систематичний виклад арифметики, заснованої на десятковій позиційній системі числення. Переклад починається словами «Dixit Algorizmi» (сказав Алгорізмі). У латинській транскрипції ім'я Аль-Хорезмі звучало як Algorizmi або Algorizmus, а оскільки твір про арифметику був дуже популярний в Європі, ім'я автора стало прозивним —середньовічні європейські математики так називали арифметику, засновану на десятковій позиційній системі числення. Пізніше так називали всяку систему обчислень за певним правилом, тепер термін «алгоритм» означає послідовність вказівок, що задає процес обчислень, що починається з довільних початкових даних і направлений на отримання результату, який повністю визначається цими початковими даними.

Книга алгебри Аль-Хорезмі (Китаб мухтасаб ал-джабр і ва-л-мукабала) складається з двох частин — теоретичної (теорія рішення лінійних і квадратних рівнянь, деякі питання геометрії) і практичної (застосування методів алгебри в рішенні господарський-побутових, торгових і юридичних завдань — ділення спадку, складання заповітів, розділ майна, різні операції, вимірювання земель, будівництво каналів). Слово ал-джабр (заповнення) означало перенесення негативного члена з однієї частини рівняння в іншу, і саме з цього терміну виникло сучасне слово «алгебра». Ал-мукабала (зіставлення) — скорочення рівних членів в обох частинахрівняння. Успадковане від східних математиків вчення про лінійні і квадратні рівняння стало основою розвитку алгебри в Європі.

Після введення натуральних чисел, аль-Хорезмі звертає основну увагу в першій частині книги на рішення рівнянь. Розглядаючи лінійні і квадрадні рівняння він використовує поняття числа, кореня x та квадрату x². У нижченаведеному прикладі використовуються сучасні позначення, щоб допомогти читачу зрозуміти основні ідеї, слід зауважити, що у своїх роботах аль-Хорезмі не використовував жодних символів, лише слова.

Латинський переклад сторінки, яка починається зі слів Діксіт алгоритми

Спочатку потрібно звести рівняння до однієї з шести нормальних форм:

• Квадрати рівні кореням (ax² = bx).

• Квадрати рівні числу (ax² = c).

• Корені дорівнюють числу (bx = c).

• Квадрати і корені рівні числу (ax² + bx = c)

• Квадрати і числа, рівні кореню (ax² + c = bx)

• Корені і числа, рівні квадрату (bx + c = ax²)

Геометрична частина трактату присвячена, в основному, вимірюванню площ і об'ємів геометричних фігур (трикутник,квадрат, ромб, паралелограм, званий ромбоїдом, коло,сегмент кола, чотирикутник з різними сторонами і кутами,паралелепіпед, круговий циліндр, призма, конус).

Арабська математика і розвиток поняття про число.

В арабській математиці послідовно діяли дві нумерації: спочатку алфавітна, аналогічна грецькій з деякими відмінностями, пов’язаними з особливостями арабського письма, а згодом десяткова позиційна, запозичена з Індії. Мала деяке застосування і словесна нумерація, яка відображала традицію далеких часів. Позиційна десяткова система засвоюється арабами повільно, спочатку її опановують астрономи з перекладених астрономічних індійських праць «сіндхант», згодом – більш масово після появи книги аль-Хорезмі «Про індійські числа» в 9ст.

Першими оцінили переваги цієї системи купці. Таджицький філософ і природодослідник Авіценна розповідав, що в дитячому віці батько посилав його вивчати індійський рахунок до купців. До 12ст. араби повністю володіли десятковою позиційною нумерацією.

Систему числення, основану на позначенні всіх натуральних чисел десятьма знаками - цифрами, вперше описав і застосував у IX столітті талановитий син узбецького народу Магомет син Муси із Хорезму в рукописі "Арифметика індорум". У своїй книзі аль-Хорезмі детально пояснює правила операцій додавання, віднімання, множення, ділення, добування квадратного кореня в новій нумерації. На відміну від алфавітної нумерації, крім зручності обчислень, у новій нумерації переважав елемент чіткої визначеності, послідовності дій і правил, що врешті-решт, дало назву та смислу поняттю «алгоритм».

Араби, познайомившись із цією нумерацією першими, по гідності її оцінили, засвоїли й перенесли в Європу. Одержавши назву арабської, ця система в XII столітті нашої ери поширилася по всій Європі й будучи простіше й зручніше інших систем числення, швидко їх витиснула. Сьогодні десятковими цифрами виражаються час, номери будинків і телефонів, ціни, бюджет, на них базується метрична система заходів.

Основою цієї системи є число десять. Основою системи числення називається число, яке означає, у скільки разів одиниця наступного розрядку більше за одиницю попереднього.

Загальновживана форма запису числа є насправді не що інше, як скорочена форма запису розкладу за степенями основи системи числення, наприклад

130678=1*10⁵+3*10⁴+0*10³+6*10²+7*10¹+8

Тут 10 є основою системи числення, а показник степеня - це номер позиції цифри в записі числа (нумерація ведеться зліва на право, починаючи з нуля). Арифметичні операції у цій системі виконують за правилами, запропонованими ще в середньовіччі. Наприклад, додаючи два багатозначних числа, застосовуємо правило додавання стовпчиком. При цьому все зводиться до додавання однозначних чисел, для яких необхідним є знання таблиці додавання.

Арабська геометрія

Ознайомившись з грецькою геометрією через переклади грецьких математичних творів, араби швидко засвоїли грецькі досягнення і включились у власні дослідження, проявивши критичний підхід і оригінальність. Вони розробили методи обчислення площ і об’ємів за допомогою методу вичерпування, їх увагу привертає проблема п’ятого постулату, методи геометричних побудов, застосування геометричних методів до розв’язування арифметико-алгебраїчних задач тощо, тобто у багатьох напрямках вони удосконалили та розвинули геометрію.

Найбільших успіхів у математиці досяг согдієць Мухаммед ібн Муса аль-хорезмі (тобто, родом з Хорезма - з берегів Сирдар'ї). Він працював у першій половині IX століття і був улюбленцем найвченішого з халіфів - Маамуна (сина знаменитого Гаруна аррашида). Головна книга Хорезмі названа скромно: "Навчання про переноси і скорочення", тобто техніка рішення алгебраїчних рівнянь. По-арабськи це звучить "Ільм аль-джебр валь-мукабала"; звідси виникло наше слово "алгебра". Інше відоме слово – "алгоритм", тобто чітке правило рішення задач визначеного типу – виникло від прозвання "аль-хорезмі". Третій відомий термін, введений у математику знаменитим согдійцем – це "синус", хоча в цій справі не обійшлося без курйозу.

Геометричний зміст синуса – це половина довжини хорди, що стягає дану дугу. Хорезмі назвав цю річ красиво і точно: "тятива спису"; по-арабськи це звучить "джейяб". Але в арабському алфавіті є тільки приголосні букви; голосні зображуються "огласовками" – рисками, як наші лапки і коми. Мало знаюча людина, читаючи арабський текст, нерідко плутає огласовки; так трапилось з перекладачем книги Хорезмі на латинь. Замість "джейяб" – "тятива" – він прочитав "джиба" – "бухта"; по-латинському це пишеться "sinus". З тих пір європейські математики використовують це слово, не піклуючись про його споконвічний зміст.

У наступні століття вчені Ближнього і Середнього Сходу продовжували розвивати спадщину Еллади, намагаючись об'єднати його з новим алгебраїчним вченням. При цьому індійські математики більше ухилялися в арифметику, ступаючи по стопах Діофанта. Навпроти, арабські учені слідували шляхом Архімеда. Вони намагалися розібратися в новому світі кубічних рівнянь: класифікували їх, виділяючи ті, котрі розвязуються так само просто, як квадратні рівняння.

Найвищих успіхів у цій області досяг учений поет Омар Хайям з Нішапура (1048-1131). Вірші він писав персидською, наукові трактати – арабською, а в службових справах користався тюркською мовою. У 11 столітті тюрки-сельджуки захопили велику частину Ірану і візантійських володінь у Малій Азії. На цих землях нові народи освоювали і розвивали спадщину всіх попередників – від вавілонян до арабів.

Потерпівши невдачу в прямому пошуку коренів довільного кубічного рівняння, Омар Хайям відкрив кілька способів наближеного обчислення цих коренів. Це була блискуча ідея: добратися до невідомих чисел, використовуючи добре знайомі криві! Як тільки (у 17 столітті) Рене Декарт додав до неї другу ідею – описати будь-яку криву за допомогою чисел – народилася аналітична геометрія, у якій розвязування алгебраїчних рівнянь злито воєдино з теорією чисел і з наочною геометрією. Передчуваючи цей зв'язок, Омар Хайям поставив багато цікавих обчислювальних дослідів. Він знайшов наближені способи розподілу окружності на 7 чи 9 рівних частин; склав докладні таблиці синусів і з великою точністю обчислив . Хайям здогадався, що це число ірраціональне, і навіть не квадратичне – але довести цю гіпотезу не зміг. Хайям замінив п’яту аксіому твердженням: «Дві збіжні прямі (тобто ті, які наближаються одна до одної) перетинаються і неможливо, щоб вони віддалилися одна від одної в тому напрямку, в якому вони наближаються». О.Хайям розглядає чотирикутник – пізніше його названо чотирикутником Саккері Джероламо (1667-1733) – утворений відрізком АВ, з кінців якого проведені рівні перпендикуляри АС і ВД, і відрізком СД. Хайям спочатку доводить рівність двох верхніх кутів С і Д чотирикутника АВСД, потім формулює три гіпотези: а) верхні кути С і Д гострі, б) кути С і Д тупі, с) кути С і Д прямі. Гіпотези а і б зумовлюють певну суперечливість. Отже, лишається гіпотеза с. На відпочинку від таких праць Омар Хайям писав досить смутні вірші.

Брати Бану Муса (Хст.) у працях «Книга ви вимірювання плоских і кульових фігур» і «Книга трьох братів про геометрію» досліджували питання щодо площі круга, встановивши межі для : 3 << 3 (як і в Архімеда). Для розв’язування задачі про трисекцію кута вони використовували циркуль і спеціальну лінійку, винайшли спеціальний інструмент для визначення середнього пропорційного між двома певними величинами.

Сабіт ібн Корра (836-901) обчислював площу параболічного сегмента методом вичерпування за допомогою інтегральних сум, об’єми тіл обертання, проявивши при цьому віртуозне володіння методом. По суті, він вперше користувався методом, еквівалентним інтегралу з дробовим показником n= . При обчисленні об’єму параболоїда обертання Ібн-аль-Хайсам (965-1039) вперше обчислив величину, еквівалентну інтегралу

Для потреб астрономії розвивали сферичну геометрію, за допомогою циркуля та лінійки виконували різноманітні побудови, наприклад розбиття квадрата на суму кількох квадратів і складання одного квадрата з деякого числа менших квадратів та ін.

Арабські математики зробили також свій внесок в теорію паралельних ліній на площині. Історія цієї теорії починається водночас з появою твору «Початки» Евкліда, який першим досить насторожено поставився до аксіоми паралельних: «Через задану точку можна провести не більш ніж одну пряму, паралельну заданій прямій» у формулюванні Плейфера (1748-1819), яке еквівалентне формулюванню Евкліда, хоча й більш просте. До 1800 р. в історії цієї аксіоми можна виділити два напрями: 1) спроби довести її як теорему на основі чотирьох інших аксіом; 2) спроби замінити її простішою й інтуїтивно зрозумілою аксіомою.

Математика і астронома Мухаммеда Тарагай Улугбека (Улуг-бек означає - великий князь) (1394—1449 рр.) називали татарським принцем, бо він був онуком великого татарського завойовника й полководця Тімура (або Тамерлана).

Улугбек організував велику математичну школу і запросив до неї, для наукової роботи видатних учених з різних міст своєї держави. У школі працювали Джемшид Пяседдін ал-Каші, уродженець Малоїг Азії Салахеддін ібн Мухаммед Казізаде ар-Румі, Алаеддін Алі ібн Мухаммед ал-Кашчі, абу ал-Алі ібн Мухаммед ібн Хусейн ал-Бірджанді. Улугбек не тільки очолював школу, а й сам активно працював у ній.

У самаркандській обсерваторії було складено знамениті «Нові астрономічні таблиці». Вони відрізнялись особливою точністю і повнотою. Таблиці синусів розміщені з інтервалами через 1’, таблиці тангенсів до 45° — через 1, а далі - через 5. Варто нагадати, що цими таблицями вчені користувались до останнього часу. Вони містили каталог положення 1019 зірок і таблиці руху планет. Учений ал-Каші склав перською мовою так званий «Зідж Хакані». У Самаркандській школі значне місце займала обчислювальна математика особливо при розв'язуванні числових рівнянь і задачі трисекції кута. Ал-Каші написав ґрунтовну працю «Ключ арифметики», в якій вперше в історії математики знайшов значення л з 17 правильними десятковими знаками. До такого результату європейські вчені (ван Роумен) прийшли лише наприкінці XVI ст. У цій же праці ал-Каші детально розглядає питання про вимірювання площі круга, пов'язуючи його з обчисленням числа π.

Самаркандська школа існувала не дуже довго, тому що її доля цілком залежала від становища Улугбека. Один з його синів був незадоволений миролюбною політикою батька, а також тим, що Улугбек більшість часу віддає науці. Підбурюваний релігійними фанатиками, він пішов війною на батька і захопив його в полон. 27 жовтня 1449 р. один з фанатиків підступно вбив Улугбека. Обсерваторія була зруйнована, обладнання і бібліотека знищені. Поховали Улугбека в Самарканді, у великому мавзолеї-гробниці, що являє собою багатоповерхову вузьку споруду, з видовженими вікнами, заскленими різноколірним склом, з чудовими колонами. Всередині мавзолею на першому поверсі в красиво оздобленій невеликій кімнаті стоїть саркофаг, в якому похований Улугбек. Сотні людей відвідують мавзолей, віддаючи шану великому вченому.

Мат. Європейського середгьовіччя.Леонардо Фібоначчі та його книга про Абак.

Леона́рдо Піза́нський(італ. Leonardo Pisano, близько1170 — близько1250^[1]), відоміший якФібоначчі(Fibonacci) — італійськийматематик 13 століття, автор математичних трактатів, завдяки якимЄвропадовідалася про вигадану індійцямипозиційну систему числення, відому зараз як арабські цифри. Леонардо розглянув також ідею так званих чисел Фібоначчі і вважається одним з найвидатніших західних математиків Середньовіччя^[2].

Леонардо Пізанський найбільше відомий під прізвиськом Фібоначчі (Fibonacci); про походження цього псевдоніму є різні версії. За однією з них, його батько Гільєрмо мав прізвисько Боначчі («Добромисний»), а сам Леонардо прозивався filius Bonacci («син добромисного»). За іншою, Fibonacci походить від фрази Figlio Buono Nato Ci, що в перекладі з італійської означає «хороший син народився».

Книга абака (лат. Liber abaci) — головна праця Фібоначчі(Леонардо Пізанського), присвячена викладу і пропагандідесяткової арифметики. Книга вийшла в 1202 році, друге перероблене видання в 1228 році. До наших днів дійшло лише друге видання.

Абаком Леонардо Пізанський називав арифметичні обчислення.

Леонардо побував на сході і був добре обізнаний (по арабським перекладам) з математичними досягненнями древніх греків та індійців. Він систематизував значну їх частину в своїй книзі. Книга Фібоначчі була написана простою мовою і розрахована на тих, хто займається практичним рахунком — в першу чергу торговців. Його виклад по ясності, повноті і глибині вище всіх античних і ісламських прототипів, і довгий час, до Декарта, був неперевершеним.

У творі 15 глав (книг).

Книга I вводить арабо-індійські цифри, одразу описує алгоритм множення (який в новій системі є простішим, ніж в старій римській) і показує, як перетворити числа зі старої системи в нову.

Варто відзначити, що Фібоначчі вводить як самостійне числонуль (zero), назва якого походить від zephirum, латинської форми «ас-сіфр» (порожній).

Книга II містить численні практичні приклади грошових розрахунків.

У книзі III викладаються різноманітні математичні задачі — наприклад, китайська теорема про залишки, досконалі числа,прогресії і т.п.

У книзі IV даються методи наближеного обчислення і геометричної побудови коренів та інших ірраціональних чисел.

Далі йдуть різноманітні застосування і рішення рівнянь. Частина завдань на підсумовування рядів. Для контролюобчислень по модулю наводяться ознаки подільності на 2, 3, 5, 9. Викладена теорія подільності, в тому числі найбільший спільний дільник і найменше спільне кратне.

Саме тут наводиться завдання про кроликів, що приводить до знаменитого ряду Фібоначчі.

Багато важливих завданнь уперше відомі саме з книги Леонардо; проте навіть при викладенні класичних завдань він вніс багато нового. Методи розв'язання рівнянь часто оригінальні, по суті алгебраїчні, хоча символіка відсутня. У багатьох питаннях Леонардо пішов далі китайців. Фібоначчі, вперше в Європі, вільно оперує з від'ємними числами, тлумачачи їх в індійському стилі, як борг. Самостійно відкрив кілька чисельних методів (деякі з них, втім, були відомі арабам).

«Книга абака» справила величезний вплив на поширення математичних знань в Європі, служила підручником, довідником і джерелом натхнення європейських вчених. Особливо неоціненна її роль у швидкому поширенні в Європі десяткової системи та індійських цифр.

Йордан Неморарій та Томас Брадварін Йордан Неморарій ( лат. Jordanus Nemorariusабо лат. Jordanus de Nemore ) - МатематикXIII століття. Про особу Йордану точних відомостей немає. Можливо, що це був не хто інший, як Йордан Саксонський, генерал чернечого ордену домініканців, у свій час жив в Парижі і помер у 1237 році.

Трактат Йордану Неморарія "Про елементи арифметичного мистецтва" (De elementis arismetice artis) став одним з найбільш поширених в Західній Європі підручників і після введення друкарства витримав кілька друкованих видань. Його головним джерелом і взірцем була арифметика Боеція. Чудовою особливістю цього твору є постійне вживання в ньому літер для позначення чисел.

У трактаті "Пояснення алгоритму" (Algorismus demonstratus) розглядається рахунок в різних системах: словесне числення за десятковою системою з поділом чисел на пальцеві від 1 до 9 і на суглобові різних порядків (десятки, сотні, тисячі і т. д.); індійський письмовий рахунок; дії над цілими числами; дробу звичайні і шестидесятеричной і дії над ними; нарешті, дії з пропорціями.

Трактат "Про дані числах" (De numeris datis)містить 115 завдань. Зміст завдань I книги може бути представлено у формі пропозиції: якщо дані два квадратних рівняння з двома невідомими, то дані і самі невідомі. II книга присвячена певним завданням першого ступеня, що вирішуються або за допомогою пропорцій, або за правилом простого помилкового положення. III книга займається завданнями з багатьма невідомими, вирішити з допомогою пропорцій і добування квадратного кореня. У IV книзі розглядаються квадратні рівняння з одним та двома невідомими і найпростіше кубічне рівняння x³ = a .

Йордану належить геометричний трактат "Про трикутниках" (De triangulis). I книга містить у собі різні пропозиції з трикутнику, а на початку деякі визначення. II книга займається завданнями розподілу відрізків прямої лінії і прямолінійних фігур. III книга розглядає коло, а VI книга - вписані і описані многокутники, серед завдань IV книги знаходяться також завдання квадратури кола і трисекции кута.

В "Освідченні планісфери" (Demonstratio de plana spera) Йордан доводить, щостереографічна проекція всякого належить кулі кола на площину також є кругом.

У трактаті "Про тяжкості" (De ponderibus)розглядається рівновага вантажів на важелі і на похилій площині і вводиться якийсь смутний аналог принципу віртуальних переміщень.

Є також ряд трактатів, приналежність яких Йордану Неморарію вважається сумнівною.

Лука Пачолі та його твір Сума знань з арифметики, геометрії, відношенням і пропорційності.

Фра Лука Бартоломео де Пачолі абоПачолі ( італ. Fra Luca Bartolomeo de Pacioli), ( Борго Сан Сеполькро, 1445 - Борго Сан Сеполькро, 19 червня 1517) - італійськийматематик, один з основоположників сучасних принципів бухгалтерії.

Пачолі народився близько 1445 в невеликому містечку Борго Сан-Сеполькро на кордоні Тоскани і Умбрії. Підлітком він був відданий на навчання в майстерню знаменитого художника П'єро делла Франческа. Тут його помітив великий італійський зодчий Леон Батіста Альберті, який в 1464 році рекомендував молодої людини багатому венеціанському купцеві Антоніо де Ромпіазі в якості домашнього вчителя. У Венеції Пачолі відвідує лекції знаменитого математика Доменіко Брагадіно в школі Ріальто. У 1470 році він закінчив свою першу книгу, яку написав для своїх вихованців - підручник комерційної арифметики. У цьому ж році він залишив Венецію і перебрався до Риму, де був прийнятий Альберті і оселився в його будинку. Однак через два роки Пачолі покинув Рим і прийняв чернечий постриг, ставши францисканцем.

З 14 жовтня 1477 по 11 грудня 1480 року - професор в університеті Перуджі, де читає лекції з алгебри, геометрії. Розгорнуті конспекти двох курсів: "Алгебра" і "П'ять правил Платона" були оформлені їм у вигляді окремої книги, яку автор присвятив "своїм люб'язним учням, відмінним і славним юнакам Перуджі". Потім протягом восьми років він живе в Зорі (нині - Задар в Хорватії), де займається теологією і математикою, іноді здійснюючи у справах ордена поїздки по інших містах Італії.

В 1494 р. Пачолі публікує на італійській мові математичний працю під назвою "Сума арифметики, геометрії, дробів, пропорцій і пропорційності" (Summa di arithmetica, geometrica, proportione et proportionalita),присвячений герцога УрбінськогоГвідобальдо да Монтефельтро. У цьому творі викладаються правила і прийоми арифметичних дій над цілими і дробовими числами, пропорції, завдання на складні відсотки, рішення лінійних, квадратних і окремих видів біквадратних рівнянь. Примітно те, що книга написана не на звичайній для вчених праць латині, а на італійській мові.

В арифметичній частини "Суми" викладаються прийоми виконання арифметичних дій; ця частина спирається на численні "Книги абака", що належали різним авторам. Алгебраїчні задачі, які вирішуються в "Сумі", не виходять за межі кола завдань на лінійні і квадратні рівняння, рассматривавшегося в арабських трактатах по "алгебри та альмукабале"; в Європі ці завдання були відомі по "Книзі абака"Леонардо Пізанського (1180-1240). Із завдань, які привернули увагу математиків наступних поколінь, слід зазначити завдання про розподіл ставки при незавершеною грі, яку сам Лука вирішив неправильно. Мабуть, саме істотне нововведення Пачолі полягає в систематичному використанні синкопованих алгебраїчній запису - своєрідної попередниці подальшого символічного числення. Книга містить таблицю монет, ваг і мір, прийнятих в різних частинах Італії, а також керівництво по венеціанської подвійної бухгалтерії. Що стосується геометричній частині Суми, вона слідує за "Практичної геометрією" Леонардо Пізанського.

В 1496 на запрошення герцога Лодовіко Сфорца приїжджає в Мілан і очолює щойно створену при Міланському університеті кафедру математики. У Мілані знайомиться зЛеонардо да Вінчі, з яким надалі дуже здружився. У Мілані Пачолі написав послання "Про божественної пропорції", адресований герцогу Лодовіко Сфорца, а Леонардо виконав до нього ілюстрації. Трактат був завершений 14 грудня 1498. До декількох рукописним екземплярів трактату, врученим властітельним особам, додавався набір правильних багатогранників та інших геометричних тіл, про які брат Лука каже, що виготовив їх власноруч. Збереглося два рукописи цього трактату - одна в Публічній бібліотеці в Женеві, друга - в Амброзіанській бібліотеці в Мілані.

В 1499, після окупації Мілана французькою армією, Лука Пачолі і Леонардо да Вінчі поїхали до Флоренцію, після чого їх шляхи розійшлися. У наступні роки Пачолі читає лекції в Пізі (1500), Перуджі (1500), Болоньї (1501-1502) та Флоренції (1502-1505).

У 1508 році у Венеції Пачолі видає латинський переклад "Почав" Евкліда, що належить Джованні Кампано. Цей переклад, зроблений ще в 1259 році з арабської мови, вже видавався в 1482 році і потім кілька разів перевидавався, але видання буяло друкарськими помилками і помилками. Пачолі відредагував переклад і по цій редакції, забезпеченою численними коментарями, читав свої університетські лекції.

У 1509 році у Венеції була видана ще одна книга Пачолі: "Божественна пропорція. Твір, вельми корисне всякому проникливого і допитливому розуму, з якого кожен вивчає філософію, перспективу, живопис, скульптуру, архітектуру, музику або інші математичні предмети витягне приємне, дотепне і дивовижне вчення і розважить себе різними питаннями потаємним наук ".

В 1508, завдяки своєму давньому знайомству з татом Юлієм II, отримує посаду місцеблюстителя монастиря в рідному місті Сан-Сеполькро. Проте в грудні 1509 два ченці його монастиря передали генералу ордена лист, в якому вказували на те, що "маестро Лука невідповідний людина, щоб керувати іншими", і просили звільнити його від адміністративних обов'язків. Але підтримки у начальства вони не знайшли, і в лютому 1510 Лука Пачолі стає повноправним пріором рідного монастиря. Втім, суперечки всередині монастиря тривали і далі.

Вступ до мистецтва аналізу Франсуа Вієта.

Французький математик Франсуа Вієт народився у містіФонтенес            ( Пуату ). За фахом юрист. Вієт вперше дав єдину, послідовно проведену систему алгебраїчних символів. Вперше застосував (1591) символічні позначення не тільки для невідомих, але й для коефіцієнтів рівнянь. Для наближеного розв’язування алгебраїчних рівнянь з численними коефіцієнтами запропонував метод, подібний методу Ньютона, що виник пізніше.

Під час педагогічних занять в одній впливовій сім’ї у нього виник план нової астрономічної системи, яка мала замінити неточну, на його думку, систему Коперніка. У зв’язку з цим задумом Вієт доклав багато зусиль, щоб удосконалити тригонометрію, і досяг чудових успіхів.

Блискуче освічений, Вієт швидко просувається по службовій дробині і нарешті став радником і придворним ученим французьких королів Генріхів III і IV.

 З 1584 по 1589 рік внаслідок підступів політичних ворогів він був усунутий від придворних справ і використав своє дозвілля на написання головної праці свого життя – «Вступу до мистецтва» - аналізу великого і дуже ґрунтовно написаного твору з нової алгебри. Ця праця виходила частинами, переважно уже після смерті автора. І не була цілком завершена.

         У творах Вієта підбивається своєрідний підсумок математики епохи відродження. Найбільш виразно ця особливість виявляється в його алгебраїчних працях. У них докладно і ґрунтовно викладено відомості про рівняння 1-го – 4-го степенів.

Якщо   — корені многочлена   (кожен корінь присутній відповідно до його кратності), то коефіцієнти   виражаються в виглядісиметричних многочленів від коренів, а саме:

Іншими словами   дорівнює сумі всіх можливих  -добутків із коренів.

Якщо старший коефіцієнт многочлена  , то для застосування формули Вієта необхідно розділити всі коефіцієнти на 

Із останньої формули Вієта випливає, що якщо корені многочлена є цілими, то вони є дільниками його вільного члена, який також є цілим.

• Якщо 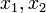  корені квадратного рівняння   то

• В частковому випадку при   (квадратне рівняння  ), то

Нові відриття алгебри А.Жірара

Рене Декарт та цого праці

Рене́ Дека́рт (фр. René Descartes, лат. Renatus Cartesius —Картезій; *31 березня 1596, Ла-Е-ан-Турен (фр. La Haye en Touraine) [зараз місто Декарт], департамент Ендр і Луара,Франція — †11 лютого 1650, Стокгольм) — французькийфілософ, фізик, фізіолог, математик, основоположниканалітичної геометрії. У математиці Декарт запровадивДекартову систему координат, дав поняття змінної величини іфункції, ввів багато алгебраїчних позначень. У фізиці він сформулював закон збереження кількості руху, запровадив поняття імпульсу сили. Декарт — автор методу радикального сумніву в філософії, механіцизму у фізиці, передтечарефлексології.

Математика

У 1637 побачила у світ головна математична праця Декарта, «Міркування про метод» (повна назва: «Міркування про метод, що дозволяє направляти свій розум і відшукувати істину в науках»).

У цій книзі викладаласяаналітична геометрія, а в додатках — численні результати валгебрі, геометрії,оптиці (у тому числі — правильне формулювання закону заломлення світла) і багато чого іншого.

Особливо слід відзначити перероблену Декартом математичну символіку Вієта, з цього моменту близьку до сучасної.Коефіцієнти він позначав a, b, c ..., а невідомі — x, y, z. Натуральний показник степеня прийняв сучасний вигляд (дробові і негативні утвердилися завдяки Ньютону). З'явилася риска над підкореневим виразом. Рівняння приводяться до канонічної форми (у правій частині — нуль).

Символічну алгебру Декарт називав «Загальною математикою», і писав, що вона повинна пояснити «все що відноситься до порядку і міри».

Створення аналітичної геометрії дозволило перевести дослідження геометричних властивостей кривих і тіл на алгебраїчну мову, тобто аналізувати рівняння кривої в деякійсистемі координат. Цей переклад мав той недолік, що тепер треба було акуратно визначати справжні геометричні властивості, які не залежать від системи координат (інваріанти). Однак і переваги нового методу були винятково великі, і Декарт продемонстрував їх у тій же книзі, відкривши безліч положень, невідомих древнім і сучасним йому математикам.

У додатку «Геометрія» були дані методи розв'язанняалгебраїчних рівнянь (у тому числі геометричні та механічні), класифікація алгебраїчних кривих. Новий спосіб завдання кривої — за допомогою рівняння — був вирішальним кроком до поняття функції. Декарт формулює точне «правило знаків» для визначення числа додатних коренів рівняння, хоча і не доводить його.

Декарт досліджував алгебраїчні функції (многочлени), а також ряд «механічних» (спіралі, циклоїди). Для трансцендентних функцій, на думку Декарта, загального методу дослідження не існує.

Комплексні числа ще не розглядалися Декартом на рівних правах з дійсними, однак він сформулював (хоча і не довів)основну теорему алгебри: загальна кількість дійсних і комплексних коренів алгебраїчного рівняння дорівнює йогостепеню. Від'ємні корені Декарт за традицією іменував помилковими, проте об'єднував їх з додатними терміном дійсні числа, відокремлюючи від уявних (комплексних). Цей термін увійшов у математику. Втім, Декарт виявив деяку непослідовність: коефіцієнти a, b, c ... у нього вважалися додатніми, а випадок невідомого знака спеціально відзначався трьома крапками ліворуч.

Всі невід'ємні дійсні числа, не виключаючи ірраціональних, розглядаються Декартом як рівноправні; вони визначаються як відношення довжини деякого відрізка до еталону довжини. Пізніше аналогічне визначення числа взяли Ньютон і Ейлер. Декарт поки ще не відокремлює алгебру від геометрії, хоча і змінює їхні пріоритети; розв'язок рівняння він розуміє як побудову відрізка з довжиною, рівною кореню рівняння. Цей анахронізм був незабаром відкинутий його учнями, передусім — англійськими, для яких геометричні побудови — чисто допоміжний прийом.

Книга «Метод» відразу зробила Декарта визнаним авторитетом в математиці і оптиці. Примітно, що видана вона булафранцузькою, а не латиною. Додаток «Геометрія» було, проте, тут же переведено на латинську і неодноразово видавався окремо, розростаючись від коментарів і ставши настільною книгою європейських учених. Праці математиків другої половини XVII століття відображають сильний вплив Декарта.