Вавилонська математика

Для множення застосовувався громіздкий комплект таблиць, окремо для множення на 1-20, 30 ... 50. Ділення m / n вони замінювали множенням m × (1 / n), а для знаходження 1 / n у них були спеціальні таблиці. Інші таблиці допомагали підносити до степеня, витягувати коріння і навіть знаходити показник ступеня n, якщо дано число виду (Ці двійкові логарифми використовувалися для підрахунку відсотків за кредитом) [2] . Без багатопудова бібліотеки таблиць ніякі розрахунки у Вавилоні були неможливі.

Для обчислення квадратних коренів вавілоняни винайшли ітераційний процес: нове наближення виходило з попереднього за формулою методу Ньютона [3] :

В геометрії розглядалися ті ж фігури, що і в Єгипті , плюс сегмент круга і усічений конус . У ранніх документах вважають ; Пізніше зустрічається наближення 25/8 = 3,125. Зустрічається також і незвичайне правило: площа круга є 1/12 від квадрата довжини кола, тобто . Вперше з'являється (ще при Хаммурапі ) теорема Піфагора , причому в загальному вигляді; вона забезпечувалася особливими таблицями і широко застосовувалася при вирішенні різних завдань. Вавилоняни вміли обчислювати площі правильних багатокутників ; мабуть, їм був знайомий принцип подібності. Для площі неправильних чотирикутників використовувалася та ж наближена формула, що і в Єгипті : .

Все ж багата теоретична основа математики Вавилона не мала цілісного характеру і зводилася до набору розрізнених прийомів, позбавлених доказової бази. Систематичний доказовий підхід у математиці з'явився тільки у греків .

Арабська математика

Чи знаєте ви, наприклад, що слово "алгебра" - арабського походження (аль-джебр)? Його ввів у науковий обіг арабський географ, математик і астроном ал-Хорезмі. До речі, ім'я цього вченого (в латинізоване формі) збереглося в сучасній математиці - "алгоритм". Арабам належать особливі заслуги в розвитку тригонометрії, інших областей математики. Арабські цифри, якими ми зараз користуємося, прийшли в Європу від арабів, які перейняли їх від індусів.

Математика і астрономія були засновані в основному на перекладах Евкліда, Птолемея і індійських сіддхант. Вони мали в Халіфаті практичну спрямованість. Показово висловлювання Мухаммеда бен Муси аль-Хорезмі (пом. після 846 р.), одного з перших багдадських математиків, на початку його знаменитого алгебраїчного трактату, присвяченого ал-Ма'муну: «Я склав коротку книгу про обчислення аль-джебр і аль- мукабале, що містить в собі прості і складні питання арифметики, бо це необхідно людям при діленні спадків, складанні заповітів, розділі майна і судових справах, в торгівлі і всіляких операціях, а також при вимірюванні земель, проведенні каналів, інженерному мистецтві та інших різновидах подібних справ ». За своїм характером математичні та астрономічні трактати - зоряні каталоги ал-Баттані, Абдаррахмана ас-Суфі (обидва - X ст.) Та ін - представляють невеликі за обсягом твори, і в складі середньовічної арабської книжкової писемності їм належить скромне місце. Арифметичні глави обов'язкові входять в той розділ творів з фикху, де розглядаються питання успадкування і розділу майна. З астрономією і рахунком пов'язані твори, присвячені місячним календарем, визначенню часу молитви та посту, визначення напрямку Кібли (напрямок в сторону Ка'би), куди молільникові належало звертатися особою. Зрозуміло, географічні, Космографіческая і енциклопедичні твори приділяли належну увагу математики та астрономії. Ці два предмети займали мізерно мало місця, якщо взагалі були, в програмі медресе; тим не менш навчальні посібники існували.

Слов'янська математика

Математичні знання східних слов’ян (від І ст. до ІV ст. н.е.). Історія східних слов’ян починається на рубежі бронзового і раннього залізного віків. Слов’яни здавна розселилися в Східній Європі і на території сучасної України. Про рівень математичних знань східних слов’ян у І – ІІ ст. н.е. свідчить грошовий обіг, який здійснювався з використанням римської срібної монети. Про рівень астрономічних знань ( які в свою чергу обумовлюють математичні) свідчить давньослов’янський календар, знайдений на території с. Ромашки на Київщині. Цей календар, який датується IV – V ст. н.е., було нанесено у вигляді орнаменту на стінки великого глечика. Ним охоплювався період з 1 квітня до 6 серпня і відображався своєрідний розклад сільськогосподарського циклу. Основними зафіксованими датами в календарі були: 4 червня (день Ярила), 24 червня (свято Купала), 20 липня (день бога Грому). Дні між цими датами зображалися у вигляді маленьких квадратиків, кількість яких у всіх випадках точно відповідала кількості днів, що відділяла одне свято від іншого.

Походження знань в галузі геометрії носить практичний характер. В народному мистецтві простежуються два стилі: “звіриний” і “геометричний” – створення орнаментів з трикутників, ромбів, квадратів, кругів, паралельних і перпендикулярних ліній. Використовувались знаки-символи: хрести, ромби, квадрати, кола та інші фігури. Символами влади вождів вживали залізні тризубці. Будуючи житло східні слов’яни користувались властивістю діагоналей прямокутника, вироблялись різні способи вимірювання висоти предметів, відстані до них, наприклад, при побудові кам’яних фігур ідолів (богів) 2-3 м заввишки, князівські могили насипали іноді висотою до десятків метрів.

Знайомство з народними мірами і засобами вимірювання дає можливість вивчити світ просторових уявлень людей, допомагає вивчити їх геометричні знання і вміння обчислювати. З розвитком сільськогосподарських робіт вдосконалюються засоби визначення площі прямокутника, трапеції, трикутників. Деякі джерела свідчать, що площа трапеції обчислювалась як добуток півсуми основ на меншу бічну сторону, площа трикутника – як половина добутку сторін, що містять найбільший кут. Поле довільної форми розбивали на частини, площу яких вміли визначати. В сільському господарстві і побуті були предмети різної форми: циліндричної, кубічної, прямокутного паралелепіпеда, конічна поверхня (курені). З часом вдосконалюються методи обчислення об’ємів таких тіл.

Слов'янські цифри - цифри, що застосовувалися древніми слов'янами для позначення чисел в алфавітній системі нумерації, що виникла в X в. Вважають, що алфавітне позначення чисел було введено одним з укладачів слов'янського алфавіту - Кирилом (помер у 869 р.).

Система позначення чисел була побудована за типом іонійської, якою користувалися візантійці; числові значення отримали лише літери, що відповідали буквам грецького алфавіту. Ця слов'янська система іменувалася кирилицею.

У другому слов'янському способі позначення чисел - глаголиці - подібності з іонічної системою немає. Там числові значення букв строго відповідають їх алфавітним порядком. В обох системах для виділення в тексті чисел над кожною літерою або треба всім числом ставилося особливий знак (титло).

У слов'янській мові для найменування вищих десяткових розрядів вживалися назви «мале число», в якому назви не йшли далі 106, і «велике число», в яке входили числа до 1050. При цьому одні й ті ж назви позначали в обох системах різні числа. Так, тьма позначала 10 000 в малому числі і 1000000 у великому числі. Легіон позначав в малому числі 10 тем, а в великом числі - тьму тим і т. д. 1050 називали колодою.

Букви алфавіту, відповідні числам 1-9, обведені кружком, позначали темряви, обведені кружком з точок - легіони, а гуртком з променів - леодр (леодр - в малому числі дорівнював 10 легіонам, тобто 1 000, а в великом - 1024 = легіон легіонів). Леодр леодр (1048) називався вороном.

МАТЕМАТИКА ДРЕВНЬОГО КИТАЮ

Перші дійшли до нас китайські писемні пам'ятки відносяться до епохи Шан (XVIII-XII ст. До н. Е..). І вже на гадальних кістках XIV в. до н. е.., знайдених в Хенань, збереглися позначення цифр.

Розвиток науки продовжилося після того, як в XI в. до н. е.. династію Шан змінила династія Чжоу. У ці роки виникають китайська математика і астрономія. З'явилися перші точні календарі та підручники математики. «Винищення книг» імператором Цинь Ши Хуаном (Ши Хуанді) не дозволило раннім книг дійти до нас, проте вони, швидше за все, лягли в основу подальших праць.

З царювання династії Хань (208 до н. Е.. - 220 н. Е..) Древні знання стали відновлювати і розвивати. У II ст. до н. е.. опубліковані найбільш древні з дійшли до нас творів - математико-астрономічний «Трактат про вимірювальному жердині» і фундаментальну працю «Математика в дев'яти книгах» (Цзю чжан суань шу "九章 算术"). Тлумачення цього трактату було полегшено завдяки відкриттю тексту "Суань шу шу" 筭 数 书 в 1983-84 рр.. (Чжанцзяшань, пров. Хубей), що відноситься приблизно до цього ж періоду.

Найбільш змістовне математичний твір стародавнього Китаю - «Математика в дев'яти книгах». Це слабо узгоджена компіляція більш старих праць різних авторів. Книга була остаточно відредагована фінансовим чиновником Чжан Цаном (помер в 150 р. до н. Е..) І призначена для землемірів, інженерів, чиновників і торговців. У ній зібрані 246 завдань, викладених у традиційному східному дусі, т.е рецептурно: формулюється завдання, повідомляється готову відповідь і (дуже стисло і не завжди) вказується спосіб вирішення.

нумерація

Цифри позначалися спеціальними ієрогліфами, які з'явилися в II тисячолітті до н. е.., і знамено їх остаточно встановилося до III в. до н. е.. Ці ієрогліфи застосовуються і в даний час. Китайський спосіб запису чисел спочатку був мультиплікативним. Наприклад, запис числа 1946, використовуючи замість ієрогліфів римські цифри, можна умовно представити як 1М9С4Х6. Однак на практиці розрахунки виконувалися на лічильної дошці суаньпань, де запис чисел була іншою - позиційної, як в Індії, і, на відміну від вавилонян, десятковій. [1]

Китайська лічильна дошка за своєю конструкцією аналогічна російським рахунками. Нуль спочатку позначався порожнім місцем, спеціальний ієрогліф з'явився близько XII століття н. е.. Для запам'ятовування таблиці множення існувала спеціальна пісня, яку учні заучували напам'ять.

Основні досягнення

Престиж математики в Китаї був високий. Кожен чиновник, щоб отримати призначення на посаду, здавав, крім інших, і іспит з математики, де зобов'язаний був показати вміння вирішувати завдання з класичних збірок.

У I-V ст. н. е.. китайці уточнюють число П - спочатку як, потім як 142/45 = 3,155 ..., а пізніше (V століття) як 3,1415926, причому відкривають для нього відоме раціональне наближення: 355/113.

У цей час китайцям вже було відомо багато чого, в тому числі:

вся базова арифметика (включаючи знаходження найбільшого спільного дільника і найменшого спільного кратного);

дії з дробами і пропорції;

дії з негативними числами (фу), які трактували як борги;

рішення квадратних рівнянь.

Був навіть розроблений метод фан-чен (方程) для розв'язання систем довільного числа лінійних рівнянь - аналог класичного європейського методу Гауса. [2] Чисельно вирішувалися рівняння будь-якого ступеня - способом тянь-юань (天元 术), що нагадує метод Руффіні-Горнера для знаходження коренів многочлена [3].

У галузі геометрії їм були відомі точні формули для визначення площі та обсягу основних фігур і тіл, теорема Піфагора і алгоритм підбору піфагорових трійок.

У III столітті н. е.. під тиском традиційної десяткової системи мір з'являються і десяткові дроби. Виходить «Математичний трактат» Сунь-Цзи. У ньому, крім іншого, вперше з'являється задача, якій пізніше в Європі займалися найбільші математики, від Фібоначчі до Ейлера і Гауса: знайти число, яке при діленні на 3, 5 і 7 дає відповідно залишки 2, 3 і 2. Завдання такого типу нерідкі в теорії календаря.

Математика Київської Русі.

Головними джерелами, які даютьуявлення про про рівень математичних знань у Київській Русі є писемні твори, що містять деякі математичні відомості, а також пам’ятки зодчества, ремесла і народна творчість.

Найдавнішим пам’ятником математичних знань усієї епохи Київської Русі є математичний твір монаха Кирика Новгородського “Вчення бачити людині всіх років” (1134). Цей твір присвячено арифметико-хронологічним розрахункам. В ньому автор показує, як визначати кількість років, місяців, тижнів, днів і годин, що пройшли від створення світу; кількість високосних років; кількість в році звичайних і місячних місяців, тижнів, днів і годин; кількість годин в одному дні. Для визначення днів, на які припадають християнські свята, Кирик розглядає “вчення про індикту” (рахунок п’ятнадцятиріччями), “сонячний круг” (період у 28 років, після якого новий рік юліанського календаря припадає на той же день тижня), “місячний круг” (період у 19 років, після якого місячні фази припадають на ті ж числа місяця юліанського календаря), “великий круг” – період в 532 роки (532 = 1928).

Аналізі цього твору свідчить про те, що його автор володів чотирма діями арифметики, знав дії з дробовими числами, мав уявлення про геометричну прогресію.

В збірнику “Руської Правди” (перший збірник законів за часів Ярослава Мудрого) міститься 47 статей, з яких 36 містять відомості про грошову систему (1 гривня = 20 ногатам = 25 кунам = 50 резанам). В цьому та інших збірниках того часу містяться задачі про відсотки на позичені гроші, подаються сільськогосподарські розрахунки, розглядаються задачі, розв’язання яких зводиться до геометричної прогресії і чисел Фібоначчі.

Ймовірно саме такі математичні знання мали освічені люди в Київській Русі. (Порівняйте з розвитком математики в Стародавніх Єгипті, Вавилоні і Греції). Чи були в Київській Русі школи? Володимир Святославоич ще в 988 р. заснував школу “книжного учения”. А в 1060 р. Ярослав Мудрий “собра от старост и поповых детей 300 учити книгам”. Навіть окремі жінки були грамотні. Наприклад, дочка чернігівського князя Єфросиня “не в Афинеях учися, но афинейские премудрости изучи…философию же и историю и всю грамматикою, числа и кругов обхождение”. Ото ж були в Київській Русі і школи, було й ідивідуальне навчання. Але математики як окремого навчально предмета в них не вивчали. Окремих дітей і юнаків знайомили тільки з нумерацією та простішими арифметичними діями. Починаючи з 10 ст., числа на Русі позначали кириличними буквами-алфавітом, запровадженим Кирилом та Мефодієм. Ця нумерація схожа до іонійської. тільки букви мали інші форми.

Деякі відомості про рівень математичних знань в Київській Русі можна одержати, вивчаючи її архітектуру і ремесло, а також народне мистецтво. Зодчі Київської Русі знали арифметику і геометрію. Для створення архітектурної форми вони використовували геометричні побудови, найпростіші відношення: 1:2, 2:3, 3:4, 4:5, 5:6, а також золотий переріз. Геометричні знання передавалися здебільшого майстровими людьми. Добрі будівельники Київської Русі вміли провішувати прямі, будувати прямі кути, проводити кола, ділити їх на кілька рівних частин, проводити паралельні прямі і т. ін. Ці знання передавались від майстра до учня індивідуально, як секрети майстерності. Ніяких доведень теорем вони, звичайно, не розглядали.

Вважається, що основою архітектурної творчості була математика, зокрема геометрія. Деякі знання з математики мали також давньоруські майстри. В Київській Русі зустрічається посуд різної форми, який змінювався. Зміну геометричних форм можна прослідкувати, наприклад, по фібулам (металічна застібка для одягу). Перша фібула складається з двох щитків (у вигляді півкола і ромбічного), в другій – півколо ділиться на 5 рівних частин, в третій – на 8, в четвертій, п’ятій і шостій – на 5, в сьомій – на 6 частин. Знахідки в давньоруських курганах свідчать, що в ХІІ – ХІІІ ст.ст. були розповсюджені орнаменти різних прикрас, що виконувались за допомогою металевого зубчастого коліщатка з 24 зубцями. А для цього потрібно було поділити коло на 24 рівні частини.

Гончарні клейма Х – ХІ ст.ст. мали певну геометричну форму: квадрат, концентричні кола, часто поділені на чотири, шість, вісім рівних частин. Різноманітні форми зустрічаються в продукції різних видів ремесел: шлеми, браслети та інші прикраси, посуд. Майстри Київської Русі знали плоскі фігури – квадрат, прямокутник, паралелограм, ромб, круг, а також геометричні тіла – куб, паралелепіпед, піраміда, циліндр, конус, куля, призма з різними основами. Вони використовували поділ кола на 4,5,6,8 і 24 частини.

Як свідчать стародавні пам’ятки історії, давні слов’яни користувались алфавітною нумерацією. Слов’янська кирилівська нумерація будувалась аналогічно до грецької (іонійської) на основі алфавіту (кирилиці) і складалася з 27 головних символів для позначення одиниць, десятків і сотень. Для відмінності символів, що виражають числа від літер над ними ставили знак  “титло”. Не використовувалась у якості цифри друга літера кирилиці Б. Для позначення одиниць вищих розрядів існувала система допоміжних символів, які означали: 10³тисяча, 10⁶ – тьма, 10¹² – легіон , 10²⁴ – леодр, 10⁴⁸ – ворон. Джерела ХІ ст. свідчать про те, що слов’яни на той час вже були обізнані з індійською нумерацією.

У Київській Русі були поширені такі одиниці довжини: “п’ядь, чверть, лікоть, сажень, верста, поприще. П’ядь – відстань від кінця великого пальця до вказівного, дорівнювала вона приблизно 19 см. Чверть або велика п’ядь від кінця великого пальця до мізинця ( 23 см). Ліктем називалась відстань від кінця витягнутого середнього пальця руки до ліктьового згину, приблизно 46 см. Різних сажнів існувало біля десяти (від 151 см до 216 см). Верста дорівнюваоа приблизно 500 сажням. Поприще – інша назва версти. Однак, у різні часи і в ріхних місцях співвіднощення між різними значеннями величин були різними, зокрема й такими: 1 верста = 750 сажнів = 2250 ліктів = 4500 п’ядей.

Окремої міри площі не існувало. Налог чи данину брали тоді не з площі поля, а “з сохи”, з “рала”. Об’єми сипучих тіл виміряли кадями, половиками, убороками, луканами, а рідини – відрами, бочками і т.п.

Головна грошова одиниця – гривня, була і вагою, і грошовою одиницею. В давній Русі були гривні вагою 96 або 48 золотників (1фунт - 96 золотників).

Проблеми історії математики та інформатики

Відкриті математичні питання

Нерозв'язані пробле́ми (або Відкриті проблеми) —гіпотези, що видаються вірними, але дотепер не доведені.

У науковому світі популярна практика складання відомими вченими або організаціями списків відкритих проблем, актуальних на сучасний момент. Зокрема, відомими списки математичних проблем є: Проблеми Гільберта, Проблеми Ландау, Проблеми тисячоліття. Згодом опубліковані проблеми з такого списку можуть бути розв'язані і, таким чином, втратити статус відкритих. Наприклад, більшість із проблем Гільберта, представлених ним у 1900 році, тепер так чи інакше розв'язані.

Гіпотези про прості числа

• Сильна проблема Гольдбаха. Кожне парне число, більше 2, можна представити у виді суми двох простих чисел.

• Слабка проблема Гольдбаха. Кожне непарне число, більше 5, можна представити у виді суми трьох простих чисел (доведена для всіх досить великих непарних чисел).

• Відкритим є питання нескінченності кількості простих чисел у кожній з наступних послідовностей:

Гіпотези про досконалі числа

• Не існує непарних досконалих чисел.

• Існує нескінченна кількість досконалих чисел.

[ред.]Гіпотези про дружні числа

• Не існує взаємно простих дружніх чисел.

• Будь-яка пара дружніх чисел має однакову парність.

[ред.]Інші гіпотези

• Злегка надлишкових чисел не існує.

• Паралелепіпеда з трьома цілочисловими ребрами і чотирма цілочисловими діагоналями не існує.

[ред.]Геометрія

• У задачі про переміщення канапи не доведена максимальність найкращої оцінки знизу (константи Гервера).

• Задача про 9 кола. Не існує 9 кіл, таких, що кожні два перетинаються, і центр кожного кола лежить поза іншими колами.

(Час виконання алгоритму перевірки — занадто великий)

[ред.]Алгебра

• Зворотна теорема теорії Галуа. Для будь-якої скінченної групи H існують поля F і G, такі, що G є розширенням F і Gal(G/F) ізоморфна H.

• Будь-яка скінченнопредставлена група, кожен елемент якої має скінченний порядок, — скінченна.

Для скінченнопородженої групи (більш слабка умова) це неправильно.^[1]

[ред.]Аналіз

• Стала Ейлера-Маскероні — ірраціональна.

• Числа 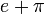  і   — ірраціональні.

• Гіпотеза Рімана. Усі нетривіальні нулі дзета-функціїлежать на прямій Re(z)=½.

• Дотепер нічого не відомо про нормальність таких чисел, як  і 

[ред.]Комбінаторика

• Існування матриці Адамара порядку, кратного 4.

• Існування скінченної проективної площини будь-якого натурального порядку.

• Гіпотеза Кацети-Хагвіста.

• Невідомо кількість обходів шахівниці конем.

[ред.]Аксіоматична теорія множин

У даний час найбільш розповсюдженою аксіоматичною теорією множин є ZFC — теорія Цермело — Френкеля з аксіомою вибору. Питання про несуперечність цієї теорії (а тим більше — про існування моделі для неї) залишається нерозв'язаним.

[ред.]Обчислювальна математика

• Визначити граничний рівень апроксимації n-стадійногометоду Рунге-Кутти (1-стадійний = метод Ейлера = O(h), 2-стадійний = модифікований метод Ейлера = O(h^2), 4-стадійний = класичний метод Рунге-Кутти = O(h^4), 5-стадійний = метод Фельберга = теж O(h^4)).

[ред.]Відомі проблеми, недавно розв'язані

• Проблема чотирьох фарб

• Велика теорема Ферма

• Гіпотеза Пуанкаре

Основні ідеї аналітичного геометрії Ферма.

До розробки розпочав новою аналітичної геометрії незалежно друг від одного й одночасно приступили два найбільших французьких мало тематика XVII в.— Ферма і Декарт. Невеликий «Введення у вивчення пласких і тілесних місць» (Adlocospianos etsolidosisagoge) Ферма було написане дещо раніше 1637 р., але життя Ферма поширювалося черезМерсепна та інших лише у рукописному вигляді. Нагадаємо, що «плоскі і тілесні місця» — терміни грецької геометрії — означали прямі і окружності і еліпси, параболи і гіперболи. Робота написана в позначенняхВиета із дотриманням однорідностіуравнений.

Ферма формулює принцип аналітичної геометрії так: «Щоразу, як у заключному рівнянні є дві невідомі величини (>quantitatesignotae), очевидна є місце, інец а такою описує пряму або ж криву лінію... Для вустановления рівнянь зручно розмістити обидві невідомі величини під деяким заданим кутом (який ми здебільшого приймаємо прямим) і ситуацію і кінець одній звеличин»[3]. Як бачимо, під невідомими величинами (координатами) Ферма розумієпрямолинейние відтинки: першу їх він щоразу позначає >NZ і алгебраически буквою А, а другу відповідно >ZI і Є. Потім за порядку рассматриваются різні плоскі і тілесні місця.

>Уравнение прямий, що проходить через початкову точку, Ферма ви водить у вигляді

D на А одно У на Є,

т. е. >dx = >by (на рис. 7 нанесена лише деякі з прямий >NI, оскільки Ферма користується позитивними координатами). Цей випадок наводиться загальне рівняння першого ступеня (із зазначеним обмеженням) і кілька далі однорідне рівняння другого ступеня, до чого тут йдеться лише про одну з двох можливих прямих. Перше приведення сутнісно зі стоїть у перетворення координат, саме у паралельному зсуві вздовж горизонтальній осі: від рівняння виду з - >dx = >by Ферма переходить до >d (>r - x) = >by, де>dr = з. Ідею перетворення координат шляхом параллельного перенесення системи Ферма краще висловлює всле дмуть прикладах: встановивши спочатку, що у прямокутної системі рівняння окружності з центром у початковій точці є b² - x² = у², він правильно характеризує загальне рівняння окружності й у зразка перетворює до основний формі рівняння

b² - 2>dx = у² + 2>rу.

І тому він робить доповнення до квадрата

>p¹ - (x + >d)² = (у + >r)², де р² = >r² + b² + >d²,

потім пише знову x замість x + >d і y замість у + >r і він здобуває

>p² - x² = у².

Слід зазначити все-таки, що Ферма обходить мовчанням питанняотрица тільних координатах, якими виявляються координати центру (->d, ->r) у цій завданню (бо >d і >r в нього позитивні). Зрозуміло, побудувати центр йому було праці та у разі.

Основні рівняння конічних перетинів є у Ферма безпосереднє вираження у термінах алгебри їх властивостей, відомих в праціАполлоиня. Для параболи це рівняння x² = >dy і симетричний у² = >dx, для еліпса (b² - x²)/y² =const (вказується, у разі непрямого координатного кута крива будееллипсом і заconst = 1), для гіперболи (b² + x²)/y² =const. Цікаво, що у малюнку в последнем разі зображені обидві галузі гіперболи, хоча знов-таки про негативні координатах щось сказано. З іншого боку, наводиться рівнянняравносторонней гіперболи >ху=с. Усе це поширюється на відповідні рівняння, доповнені лінійними членами.

На приватному прикладі рівняння b² - 2x² = 2>xy + у² Ферма розбирає і найбільш важкий випадок, коли групу старших членів містить і член з твором координат. Його міркування й побудови відповідаютьпереходу до нову систему координат X, Y з колишнім початком і віссюординат і з віссю абсцис, котра утворює кут 45° зі старою. У цьому системі Х = x, Y = x + у, отже (2b² — X²)/Y² = 2 і постать є еліпс.

Виклавши усе це, Ферма писав: «Отже ми коротко й зрозуміло виклали усе, що залишили нез'ясованим древні щодо пласких і тілеснихмест»[4]. Насправді було зроблено лише перший кроксозданию нових типів геометрії, яка, ніби між іншим, набула свогонинешнее найменування лише в кінці XVIIIв.[5]

Мілетська школа.Фалес Мілетський та його учні.

Мілетська школа (іонійська школа натурфілософії) — (давньогрецька) філософська школа, заснована Фалесом уМілеті, одному з міст Іонії, у першій половині VI ст. до н.е. Представлена Фалесом, Анаксимандром й Анаксименом.

Натурфілосо­фія стала першим філософським вченням Давньої Греції, в якому започаткувалася моральна проблематика. Вона вийшла з грецької міфології, але на відміну від неї ставила запитання не про те, хто народив усе суще, а з чого це суще вийшло, при цьому майже не розглядався моральний бік існування людини. Представниками натурфілософії були: мілетці (Фалес, Анаксимен, Анаксимандр — VI ст. до н. е.),Геракліт, елеати, піфагорійці, софісти, Емпедокл, Анаксагор іДемокрит.

У рамках натурфілософії були висунуті перші космологічні моделі світу, в яких Космос вважався жи­вим, мав розум ідушу й розвивався за своїми законами, голов­ним з яких бувЛогос (закон), а Земля зображалася здебіль­шого у вигляді диска, оточеного повітрям або водою. Космос був своєрідним абсолютним принципом, універсальним зраз­ком, що породжував подібний до нього тип людського існу­вання — гармонійна відповідність Універсуму. Вважаючи за першооснову одну з матерій — у Фалеса це вода, у Анаксимена — повітря, у Анаксимандра — невизначена матеріальна сутність (апейрон) — перші натурфілософи розглядали фізич­ні взаємодії різних речовин (взаємовідносини праматерії та руху), не приділяючи уваги моральній стороні поведінки ок­ремої людини.

На думку Геракліта (близько 544—483 рр. до н. е.), усім править Доля (необхідність), з якою тісно пов'язаний Логос (закон). Останній існує об'єктивно, не є добрим чи злим у людському розумінні, і дотримання його є істинним і муд­рим. Усе пізнається через розум, а орієнтація на чуттєве від­даляє людину від Логосу.

Людина, на думку натурфілософів, — це істота «природ­на». Вона не може пізнавати себе відокремлено від природи, а лише як складову частку її, що має всі якості цілого і змі­нюється адекватно йому. Завдяки Логосу людина пізнавала сенс головних вимог космічного ладу — спорідненість з апейроном. Якщо відбувалася несправедливість (отримання інди­відуальних рис у тому розумінні, що ці риси не виражали за­гальної справедливості), космічна необхідність виявляла себе в образі жорстокого Року, що карає. Здійснення справедли­вості відбувається згідно з нормами таліона і розуміється як «рівна відплата».

Фале́с Міле́тський(грец. Θαλῆς ὁ Μιλήσιος, прибл.624 до н. е. — 548 до н. е.) — давньогрецькийфілософдосократського періоду, математик,астроном, засновник іонійської школи натурфілософії, купець і політичний діяч.

Наукова спадщина

Фалеса вважають першим грецьким астрономом. Він передбачив сонячне затемнення (28 травня 585 до н. е.). Йому належить заслуга у визначенні часу сонцестояння ірівнодення, у встановленні тривалості року в 365 днів, відкриття факту руху Сонця відносно зірок. У наш час іменем Фалеса названо кратер на видимій стороні Місяця.

Фалес також має великі заслуги у створенні наукової математики. У нього вперше в історії математики зустрічаються доведення теорем. Якщо єгипетських землемірів задовольняла відповідь на питання «Як?», то Фалес, мабуть, першим у світі поставив питання «Чому?» й успішно відповів на нього. Нині відомо, що багато математичних правил були відкриті набагато раніше, ніж у Стародавній Греції. Але усі — дослідним шляхом. Строго логічне доведення правильності тверджень на підставі загальних положень, прийнятих за достовірні істини, було винайдено греками. Характерна і зовсім нова риса грецької математики полягає в поступовому переході за допомогою доведення від одного твердження до іншого. Саме такий характер математиці був наданий Фалесом. І навіть сьогодні, розпочинаючи доведення, наприклад, теореми про властивості ромба, ми, по суті, міркуємо майже так само, як це робили учні Фалеса.

Вважається, що Фалес першим познайомив греків згеометрією. Йому приписують відкриття і доведення ряду теорем: про поділ кола діаметром навпіл; про те, що кут, вписаний у півколо, є прямим (Теорема Фалеса про три точки на колі); про рівність кутів при основі рівнобедреного трикутника; про рівність вертикальних кутів; про пропорційність відрізків, утворених на прямих, що перетинаються декількома паралельними прямими (Теорема Фалеса (пропорційні відрізки)). Фалес установив, що трикутник повністю визначається стороною і прилеглими до неї кутами.

Фалес відкрив цікавий спосіб визначення відстані від берега до видимого корабля. Деякі історики стверджують, що для цього він використав ознаку подібності прямокутних трикутників. Фалесу приписують також спосіб визначення висоти різних предметів, зокрема пірамід, за довжиною тіні, коли сонце піднімається над горизонтом на 45 градусів.

У «Політиці» Аристотеля знаходиться фрагментарний уривок про те, як Фалес за допомогою астрономічних знань зміг передбачити врожай олив та використати цей факт в цілях власного збагачення, показавши, що філософи здатні стати багатими, хоча цього й першочергово не прагнуть. За те, що він зрозумів вплив дефіциту товарів на процес ціноутворення, його можна вважати також раннім економістом.

Усі ці досягнення принесли Фалесу славу першого мудреця серед знаменитих «семи мудреців» далекого минулого.

Піфагорська наукова школа

Школа була заснована Піфагором в Кротоні (Південна Італія) і проіснувала до початку IV століття до н. е., хоча гоніння на неї почалися практично відразу після смерті Піфагора в 500 р. По суті, це була перша філософська школа, релігійно-філософське аристократичне братство; вона мала великий вплив на грецькі поліси Південній Італії і Сицилії. Союз відрізнявся строгими звичаями і високою моральністю. Спосіб життя піфагорійців увійшов в історію: як розповідають легенди, учнів Школи завжди можна було впізнати за їх зовнішнім виглядом і благородній поведінці. Проте і вигляд, і поведінка були лише наслідком поглядів філософів на людську душу і її безсмертя, маються на увазі в тутешньої, земного життя певне виховання. У цьому вони близькі до своїх попередників - орфіки, послідовникам вчення, то звіщали найчистішу моральність і суворий аскетизм; засновником його вважається легендарний Орфей. Згідно з цими поглядами, душа людини проходить у своєму розвитку кілька етапів, зокрема ряд втілень на фізичному плані, сенс яких - придбання внутрішнього досвіду, досягнення катарсису, очищення від спадщини ранніх етапів розвитку. Цьому служили моральні принципи, яких дотримувалися піфагорійці: "Бути завжди в словах і вчинках прагни справедливим", "Хай - що найважливіше - твоїм головним суддею стане совість". Вранці та ввечері - в години, найвідповідніші для роздумів - слід було окинути уявним поглядом все, що зроблено і що ще належить зробити: "В заспокійливий сон не годиться тобі занурюватися перш, ніж знову не згадаєш про кожного сьогоднішньому справі, в чому завинив? Що міг зробити? І чого не виконав? " Піфагорійська школа поклала початок математичних наук.Числа розумілися як суть всього існуючого, їм надавався містичний зміст. Основу піфагорейської математики складає вчення про декаді: 1 +2 +3 +4 = 10. Ці чотири числа описують всі процеси, що відбуваються у світі. Зокрема, декадавідображає закони музичної гармонії: через неї виражаються основні музичні інтервали - октава (2:1), квінта (3:2), кварта (4:3). Математичний метод в сучасній науці в цьому сенсі є наслідком популяризації та демистификации піфагорійського вчення. Піфагорійцям належить вчення про музику сфер і про музичний звукоряді, що відображає гармонію Сонячної системи, де кожній планеті відповідає певна нота, а всі разом вони створюють інтервали музичної гами. Ними ж належить і початок музичної психології: музика використовувалася як засіб виховання і зцілення душі і тіла. В піфагорійській школі почали розвиватися астрономія та медицина. Нею створено безліч алегоричних коментарів Гомера, а також граматикагрецької мови. Таким чином, піфагорійців можна вважати родоначальниками гуманітарної, природничої, точної і систематичної наук.

Геометрична алгебра

Єгипет, Вавилон.

Використання геометричних креслень як ілюстрації алгебраїчних співвідношень траплялося ще Давньому Єгипті й Вавилоні. Наприклад, під час вирішення рівнянь з цими двома невідомими, одне називалося “довжиною”, інше -”шириною”. Твір невідомих називали “площею”. У завданнях, що призводять до кубічному рівнянню, зустрічалася третя невідома величина - “глибина”, а твір трьох невідомих іменувалося “обсягом”.

Але не можна дозволити геометричних термінам запровадити нашій оману. Вавилоняни мислили, передусім, алгебраїчно. Хоча вони зображували для наочності невідомі числа лініями й майданами, але останні усе ж таки завжди залишалися числами. Це виявлялося в тому, що з величинами, під назвою мають різні виміру, зверталися і з однорідними: “площа” складали зі “стороною”, від “обсягу” забирали “площа” тощо.

Рішення рівнянь у Давньому Вавилоні.

Давні єгиптяни і вавілоняни викладали свої алгебраїчні знання з числової формі. Не знали ні негативних чисел, ні, тим паче комплексних і рівняння, які мають позитивних коренів ними розглядали. Усі завдання й розв'язання викладалися словесно.

У одній з клинописних табличок зустрічається таке завдання: “Я відмінусував з площі бік мого квадрата, це 870” (легко зрозуміти, йдеться про квадратному рівнянні x²->x=870).

Рішення їх у табличці рекомендується шукати так: “Ти береш 1, число.Делишь навпіл 1, це.Умножаешь на, це. Ти складаєш це з 870, і це є, що квадратомдля.Ти складаєш, яку ти множив, з, отримуєш 30, сторона квадрата”.

Усі вересня табличці записані в60-ричной системі числення, чому ми наводимо в десяткової записи. У звичних нам позначеннях запропоновані дії приймають вид:. У цьому записи вгадується формула обчислення коренів наведеного квадратного рівняння.

Давня Греція.

Зовсім інший вигляд прийняла алгебра у Стародавній Греції. Після відкриття піфагорійцяминесоизмеримих величин креслення із засобу наочності перетворилися на основний елемент алгебри.

Найважливішим, серед приписуваних піфагорійцям 5 століття е. досягнень, було відкриттянесоизмеримих відрізків.

Виникало воно, швидше за все, з спроб знайти спільну міру діагоналі і боку квадрата.

Це відкриття вразило основипифагорейской філософії. Адже потім із нього слід, що кількість невсемогуще, бо є відтинки, стосунок яких не виражається ставленням цілих чисел (інших чисел піфагорійці було невідомо).

Виявилося, що й не виходити далеко за межіпифагорейского вчення про кількість, то багато завдань, що призводять до квадратним рівнянням, не мають числового рішення.

Навіть така проста рівняння, як x²=2, може бути вирішено ні з області цілих чисел, ані навіть у області відносин чисел. Але він чинився цілком розв'язаним у сфері прямолінійних відрізків: його рішенням було діагональ квадрата зі стороною, що дорівнює одиниці.

Не наважуючись покращити своє трактування числа, піфагорійці перейшли в галузі чисел до області геометричних величин, побудувавши відповідне літочислення. Для побудови такого обчисленняпифагорейская математика мала всім необхідними. Потрібно були лише змінити погляд в ролі креслень, перетворивши із засобу наочності в основний елемент алгебри, і логічно розмістити весь наявний матеріал.

Ця робота було виконано піфагорійцями, та її результати згодом включеніЕвклидом на другу книжку “Почав”. Нове літочислення одержало згодом назва “геометричній алгебри”. У цьому вся обчисленні величини стали зображуватися з допомогою відрізків і прямокутників, а будь-які затвердження, ідучи докази мали права існувати в тому разі, якщо вони давалися на геометричному мові. Давньогрецькі математики працювали ні з числами, і з відрізками. Тому знайти невідоме їм означало побудувати шуканий відрізок.

Арабські країни.

Виділення алгебри (як науки про рівняннях) на самостійну гілка математики відбулося арабських країнах, куди після розпаду Римська імперія перемістився центр наукової діяльності.

У першій половині IX століття Багдаді працював Мухаммед ібн Мусаал-Хорезмиал-Маджуси (Мухаммед синМуси з Хорезма з цієї родини жерців). Збереглися його твори по арифметики, алгебрі, астрономії, географії і календарним розрахунках. Найбільш поважним є трактатал-Хорезми з алгебри, коли він розробив правила перетворення рівнянь. Рівняння, звісно, був із числовими коефіцієнтами і виражалися у словесній формі. На цих конкретні прикладиал-Хорезми показує шляхи вирішення основних типів лінійних і квадратних рівнянь. У грецьких традиціях він суворо геометрично обгрунтовує власні засоби.

Післяал-Хорезми рішенню рівнянь присвячують свою працю багато арабські вчені ( Омар Хайям,ал-Бируни,ал-Каши та інших.) Вони вивчали рівняння третього й четвертого ступеня, коріння розташовані з допомогою перетину парабол, гіпербол і окружностей. У такий спосіб вирішували завдання й грецькі геометри. Але арабських учених, чия математика тяжіла до обчисленням, цікавило і чисельна значення коренів.

Франція, Англія.

>Геометрический шлях, безсумнівно, був геніальною знахідкою античних математиків. Але, на жаль, він стримував розвиток алгебри. Адже геометрично можна сформулювати лише перші ступеня (довжини), квадратні (площі) і куби (обсяги), але з вищі ступеня невідомих. Та й невідомі у разі може лише позитивними числами. Нарешті, замість алгебраїчних перетворень доводилося виробляти геометричні побудови, часто дуже громіздкі. Щоб побудувати невідоме, іноді потрібно було залишатись справжнім віртуозом - це користь геометрії, але з алгебрі.

У першій половині XVII століття значний крок уперед уарифметизации алгебри зробив французький вчений Рене Декарт. Він відокремлював вчення про числах від вчення про величинах, не дотримувався принципу однорідності і намагався звільнити алгебру від підпорядкування геометрії.

У працях європейських учених XVIIXVIII століть чітко виявляється арифметичне побудова алгебри. І якщо в “Загальної арифметиці” Ньютона велике місце ще займають геометричні докладання, то вже у “>Началах алгебри”Клеро і “Універсальної арифметиці”Эйлера все виклад алгебри мало суто арифметичний характер.

Евклід та його початки

Евклі́д (грец.Ευκλείδης; близько 365 — близько 300 до н. е.) — старогрецький математик і визнаний основоположникматематики.

Основний твір Евкліда називається «Начала». Книги з такою ж назвою, в яких послідовно викладалися всі основні факти геометрії і теоретичної арифметики, складалися раніше Гіппократом Хіосським, Леонтом і Февдієм. Проте «Начала» Евкліда витіснили всі ці твори з ужитку і протягом більш ніж двох тисячоліть залишалися базовим підручником геометрії. Створюючи свій підручник, Евклід включив в нього багато з того, що було створене його попередниками, обробивши цей матеріал і звівши його воєдино.

«Начала» складаються з тринадцяти книг. Перша і деякі інші книги передують списком визначень. Першій книзі передує також список постулатів і аксіом. Як правило, постулати задають базові побудови (наприклад, «потрібно, щоб через будь-які дві точки можна було провести пряму»), а аксіоми — загальні правила виведення при операції з величинами (наприклад, «якщо дві величини дорівнють третій, вони рівні між собою»). З сучасної точки зору, різниці між постулатами і аксіомами нема.

У I книзі вивчаються властивості трикутників і паралелограмів; цю книгу вінчає знаменита теорема Піфагора для прямокутних трикутників. Книга II, виходить від піфагорійців, присвячена так званій «геометричній алгебрі». У III і IV книгах висловлюється геометрія кіл, а також вписаних і описаних багатокутників; при роботі над цими книгами Евклід міг скористатися творами Гіппократа Хіосського. У V книзі вводиться загальна теорія пропорцій, побудована Евдоксом Кнідським, а в VI книзі вона додається до теорії подібних фігур. VII—IX книги присвячені теорії чисел і знов посилаються до піфагорійців; автором VIII книги, можливо, був Архіт Тарентський. У цих книгах розглядаються теореми про пропорції і геометричні прогресії, вводиться метод для знаходження найбільшого загального дільника двох чисел (відомий нині як алгоритм Евкліда), будується парні довершені числа, доводиться нескінченність множини простих чисел. У X книзі, що є найоб'ємнішою і найскладнішою частиною «Начал», будується класифікація іррациональностей; можливо, що її автором є Теєтет Афінський. XI книга містить основи стереометрії. У XII книзі за допомогою методу вичерпання доводяться теореми про співвідношення площ кіл, а також об'ємів пірамід і конусів; автором цієї книги за загальним визнанням є Евдокс Кнідський. Нарешті, XIII книгу присвячено побудові п'яти правильних багатогранників; вважається, що частина побудов була розроблена Теєтетом Афінським.

У рукописах, що дійшли до нас, до цих тринадцяти книг додані ще дві. XIV книга належить александрійцу Гипсиклу (біля 200 р. до н. е.), а XV книгу створено під час життя Ісідора Мілетського, будівельника храму св. Софії в Константинополі (початок VI ст. н. е.).

«Начала» надають загальну основу для подальших геометричних трактатів Архімеда, Аполлонія і інших античних авторів; доведені в них припущення вважаються загальновідомими. Коментарі до «Начал» в античності складали Герон, Порфирій, Папп, Прокл, Симплікій. Зберігся коментар Прокла до I книги, а також коментар Паппа до X книги (у арабському перекладі). Від античних авторів коментаторська традиція переходить до арабів, а потім і до Середньовічної Європи.

У створенні і розвитку науки Нового часу «Начала» також зіграли важливу ідейну роль. Вони залишалися зразком математичного трактату, що строго і систематично висловлює основні положення тієї або іншої математичної науки

Роботи Архімеда з Сіракуз.