
Лабораторная работа №7
Тема: Численное интегрирование. Приближенное вычисление геометрических величин.
Цель: научиться применять формулы приближенного вычисления интегралов (формулу трапеций и формулу Симпсона) для решения задач численного интегрирования, вычисления площади плоской фигуры, объема тел; оценивать точность приближенного вычисления интегралов
Содержание работы по вариантам:
№ вариа-нта |
Содержание задания |
Пояснения |
||||||||||||||||||||||||||||||||||||
1 |
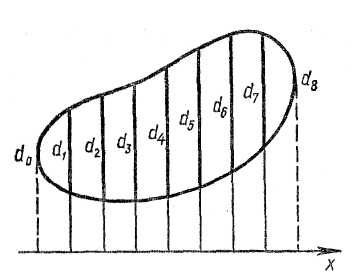
Вычислить площадь зеркала водоема по данным чертежа (см. рис.), применяя формулу трапеций (длины указаны в метрах). |
|
||||||||||||||||||||||||||||||||||||
2 |
Для
вычисления работы
пара в цилиндре паровой
машины вычисляют площадь
индикаторной диаграммы,
представляющей
собой графическое изображение
зависимости
между
давлением пара в цилиндре и ходом
поршня (см. рис.).
Ординаты точек линий ABD
и
ED
соответствующие
абсциссам
|
и |
||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
3 |
Скорость
Пользуясь графиком скорости, найти пройденный путь за время от 0 ч до 2 ч. |
R H R H 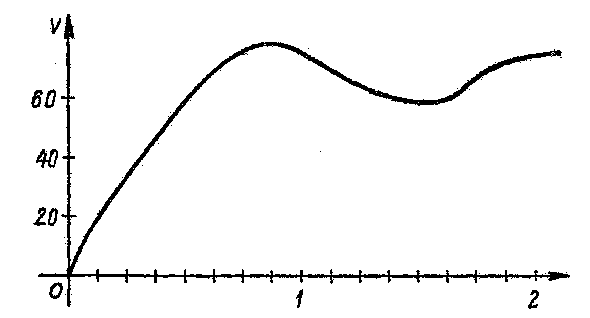
|
||||||||||||||||||||||||||||||||||||
4 |
Длина
дуги
гиперболы
|
|||||||||||||||||||||||||||||||||||||
5 |
Длина эллипса с полуосями и выражается формулой:
Вычислить
с помощью формулы Симпсона длину
эллипса, если
|
|||||||||||||||||||||||||||||||||||||
6 |
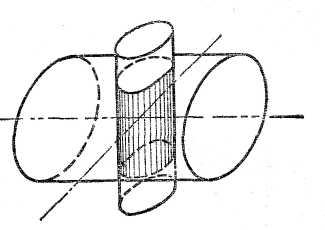
Объем
тела, вырезанного из цилиндра радиуса
Вычислить
объем такого тела, пользуясь формулой
трапеций
|
|
||||||||||||||||||||||||||||||||||||
7 |
Длина
Вычислить
,
пользуясь формулой Симпсона ( |
|||||||||||||||||||||||||||||||||||||
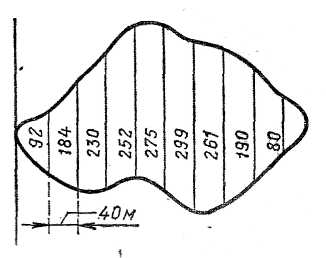
8 |
Вычислить
площадь земельного участка (см. рис.),
используя формулу трапеций. Результаты
измерений:
|
|
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
9 |
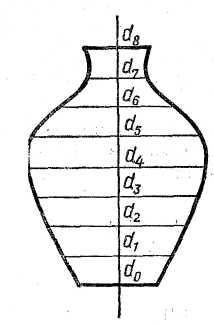
Вычислить
емкость сосуда, имеющего форму тела
вращения, осевое сечение которого
изображено на рис. Расстояние между
двумя соседними плоскостями – 1 дм,
диаметры
(в дм) круговых сечений плоскостями,
перпендикулярными оси, и площади
сечений
|
|
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
10 |
Вычислить интеграл
пользуясь малой формулой Симпсона (результат будет точным). |
|||||||||||||||||||||||||||||||||||||
Порядок выполнения работы:
записать необходимую для вычислений формулу численного интегрирования;
проанализировав условие задачи, выяснить соответствие между исходными данными и величинами, записанными в формуле;
вычислить недостающие для расчета данные, если это необходимо;
выполнить расчет по формуле;
оценить точность полученного результата по правилу удвоения.
Контрольные вопросы:
Постановка задачи численного интегрирования. Неопределенный интеграл. Определенный интеграл. Формула Ньютон-Лейбница.
Геометрический смысл определенного интеграла.
Формулы приближенного вычисления интегралов (формулы механических квадратур).
Формула Симпсона.
Графическая иллюстрация формул приближенного вычисления интегралов.
Оценка точности приближенного вычисления интегралов. Правило удвоения.
Оценка погрешности формулы трапеций.
Оценка погрешности формулы Симпсона.
Вычисление площади плоской фигуры. Общая формула для вычисления площади плоской фигуры.
Вычисление объемов тел. Общая формула для вычисления для вычисления объема тела.

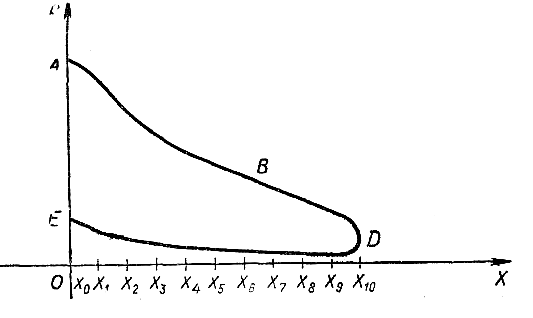 ндикаторная
диаграмма паровой
машины.
ндикаторная
диаграмма паровой
машины.
 .
Применяя формулу Симпсона, полагая
.
Применяя формулу Симпсона, полагая
 ,
где
,
где


 .
.
 ,
,