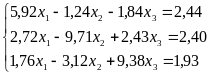Г ОУ СПО «Педколледж г. Орска»

Лабораторный практикум по дисциплине

ЧИСЛЕННЫЕ МЕТОДЫ

Специальность 050202 Информатика

3 курс, 6 семестр

Преподаватель: Косолапова О.С.

2011

ЛАБОРАТОРНАЯ РАБОТА №1

Тема: Прямая и обратная задача теории погрешностей.

Цель: научиться применять формулы для вычисления предельной абсолютной/относительной погрешности приближенного числа (производить вычисления с наперед заданной точностью).

Содержание работы по вариантам:

№ вариа-нта	Содержание задания	Пояснения
1	Объем цилиндра вычисляют по формуле . В результате измерений были получены следующие данные: см; см. Вычислить объем цилиндра, определить предельную абсолютную и относительную погрешности вычислений.	R H R H R H R H R H R H
2	Период колебаний математического маятника вычисляют по формуле . В результате измерений было получено следующее значение длины: см. Вычислить период колебаний математического маятника, определить предельную абсолютную и относительную погрешности вычислений.	см/сек2
5	Даны некоторые физические и астрономические постоянные: расстояние до звезды «Сириус» = км; масса Солнца = кг; скорость света (в вакууме) = м/сек; кратчайшее расстояние от Земли до Марса (во время великого противостояния 1971 г.) = км; заряд электрона = Кл; масса электрона = г. Оценить абсолютную и относительную погрешности этих приближенных чисел.	Предельная абсолютная погрешность числа, записанного в форме с плавающей запятой ( ), равна произведению предельной абсолютной погрешности числа на . Напр., если , то
6	Даны приближенные числа: ; ; ; . Вычислить . Определить предельную абсолютную и относительную погрешности вычислений.	При вычислениях учитывать правила верных цифр
7	Даны приближенные записи некоторых чисел: ; ; ; ; ; . Для каждого из приближенных значений найти предельные абсолютную и относительную погрешности вычислений.	Все цифры в записи числа верные; для удобства некоторые числа можно переписать в форме с плавающей запятой
9	Вычислить значение . Значения корней взять с тремя верными десятичными знаками. Оценить относительную погрешность вычислений.
10	Скорость свободного падения тела определяется по формуле , где h – высота падения, а g – ускорение свободного падения тела. В результате вычислений было получено следующее значение м/сек. Определить высоту, с которой падало тело. Указать предельную относительную и абсолютную погрешности вычислений.	м/сек2

Порядок выполнения работы:

1. записать исходные данные;

2. определить абсолютную (относительную) погрешность заданных величин;

3. по найденной абсолютной (относительной) погрешности вычислить относительную (абсолютную) погрешность заданных величин;

4. вычислить значение требуемой величины;

5. вычислить предельную абсолютную и относительную погрешности;

6. сделать вывод о степени точности исходных расчетных данных.

Контрольные вопросы:

1. Перечислите основные источники погрешностей.

2. Каким образом классифицируются погрешности в зависимости от их источников?

3. Какие способы записи приближенного значения некоторого точного числа вы знаете?

4. Какие цифры в приближенной записи числа называются значащими?

5. Какие цифры в приближенной записи числа называются верными?

6. Какие цифры в приближенной записи числа называются сомнительными?

7. Абсолютная погрешность.

8. Относительная погрешность.

9. Какой формулой выражается связь абсолютной и относительной погрешностей.

10. Каким образом определяется предельная абсолютная погрешность суммы/разности приближенных значений?

11. Каким образом определяется предельная относительная погрешность произведения/частного приближенных значений?

12. Каким образом определяется предельная относительная погрешность корня из приближенного числа?

13. Каким образом определяется предельная относительная погрешность степени приближенного числа?

14. В чем заключается прямая задача теории погрешностей?

15. В чем заключается обратная задача теории погрешностей? Что означает «произвести вычисления с заданной степенью точности»?

Лабораторная работа №2

Тема: Точные и приближенные методы решения систем линейных уравнений. Решение системы линейных уравнений методом Гаусса/методом простой итерации.

Цель: научиться решать системы линейных уравнений методом Гаусса/методом простой итерации с учетом условий применимости указанных методов

Содержание работы по вариантам:

№ вариа-нта	Содержание задания	Метод решения
1		Решить систему линейных уравнений методом простой итерации
2		Решить систему линейных уравнений методом Гаусса
3		Решить систему линейных уравнений методом простой итерации
4		Решить систему линейных уравнений методом Гаусса
5		Решить систему линейных уравнений методом простой итерации
6		Решить систему линейных уравнений методом Гаусса
7		Решить систему линейных уравнений методом простой итерации
8		Решить систему линейных уравнений методом Гаусса
9		Решить систему линейных уравнений методом простой итерации
10		Решить систему линейных уравнений методом Гаусса

Порядок выполнения работы (для решения системы методом простой итерации):

1. привести систему линейных уравнений к нормальному виду, если это необходимо;

2. проверить систему на условие применимости метода простой итерации;

3. выбрать начальное приближение , , ;

4. решить систему линейных уравнений, вычисляя первое, второе, третье,…, k-ое приближения, до тех пор, пока вычисленные значения , , и , , не будут совпадать с точностью до трех знаков после запятой ( );

5. осуществить проверку найденного решения системы.

Порядок выполнения работы (для решения системы методом Гаусса):

1. из первого уравнения системы выразить неизвестное ;

2. подставить значение во второе и третье уравнения исходной системы и получить систему двух линейных уравнений с двумя неизвестными;

3. из системы 2х линейных уравнений с 2 неизвестными выразить неизвестное ;

4. подставить значение во второе уравнение новой системы и получить уравнение с одним неизвестным ;

5. вычислить значение , , ;

6. осуществить проверку найденного решения системы.

Контрольные вопросы:

1. Что называется системой линейных уравнений?

2. Что означает «решить систему линейных уравнений»?

3. Что понимают под терминами «однородная/неоднородная система уравнений»?

4. Какой смысл вкладывают в словосочетания «система линейных уравнений совместна/несовместна»?

5. Запишите общий вид системы трех линейных уравнений с тремя неизвестными.

6. Назовите два класса методов решения систем линейных уравнений. Охарактеризуйте каждый класс.

7. Метод Гаусса (метод последовательного исключения неизвестных). Достоинства и недостатки.

8. Алгоритм метода Гаусса (схема решения системы уравнений методом Гаусса).

9. Итерационные методы (общая характеристика).

10. В чем заключается принцип сжимающих отображений.

11. Сформулируйте условия сходимости итерационного процесса.

12. Метод простой итерации. Достоинства и недостатки.

13. Практическая схема решения системы линейных уравнений методом простой итерации.

14. Система с преобладающими диагональными коэффициентами.

15. Система нормального вида.