1. Определение матрицы. Линейные операции над матрицами.

Матрицей размера (m,n) называется прямоугольная таблица чисел, имеющая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы. Элементы, стоящие на диагонали, идущей от верхнего левого угла, образуют главную диагональ. 

побочная диагональ главная диагональ

Виды матриц:

1. Матрица размерности (1,n), т.е. имеет одну строку, называется матрицей-строкой.

A=(a₁₁ a₁₂ ... a_n).

2. М атрица размерности (m,1), называется матрицей-столбцом.

3. Матрица размерности (n,n), т.е. имеет одинаковое количество строк и столбцов, называется квадратной.

Рассмотрим квадратную матрицу порядка n:

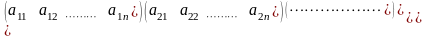
4. Квадратная матрица, все элементы которой, не входящие в главную диагональ, равны 0, называется диагональной.

5. Диагональная матрица, в которой все элементы главной диагонали – единицы, называется единичной и обозначается E.

6. Квадратная матрица, в которой все элементы над главной диагональю или под главной диагональю равны 0, называется треугольной.

7. Нулевой матрицей называют матрицу, все элементы которой равны нулю. Обозначается буквой О.

8. Матрица, полученная из данной заменой каждой строки столбцом с тем же номером, называется матрицей транспонированной к данной.

1 2 1 3

А= 3 4 А^т= 2 4

Транспонированная матрица обладает следующим свойством:

(А^т)^т =А

Операции над матрицами:

1. Сложение матриц

Суммой двух матриц одного размера называется матрица того же размера, каждый элемент которой равен сумме соответствующий элементов данных матриц.

   

Матрицы неодинаковых размерностей складывать нельзя!

2. Разница матриц

Разностью матриц A и B одинакового размера называется матрица того же размера, каждый элемент которой равен разности между соответствующими элементами данных матриц.

3. Умножение матриц на число

Произведением матриц A на число называется матрица того же размера, каждый элемент которой равен произведению соответствующего элемента данной матрицы на это число.

  

Свойства сложения и умножение матриц на число:

• А+В=В+А (коммуникативность)

• А+(В+С)=(А+В)+С (ассоциативность)

• А+0=А

• А-А=0

• 1*А=А

• α*(А+В)=αА+αВ

• (α+β)*А=αА+βА

Где А,В,С – матрицы, а β и α - числа

4. Произведение матриц

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

А) Умножение матрицы-строки на матрицу-стобец: результатом умножение стоки на столбец является матрица, состоящая из одного элемента (1х1).

 Б) Умножение двух матриц

Произведением матрицы A размера (m,n) на матрицу B размера (n,k) называется матрица размера AxB=C размера (m,k).

Для того, чтобы матрицы можно было перемножить, число столбцов первого сомножителя должно быть равно числу строк второго сомножителя. Если это требование выполнено, то произведением этих сомножителей является матрица, у которой число строк равно числу строк первого сомножителя, а число столбцов равно числу столбцов второго сомножителя.

 Найдем элементы матрицы С:

 

Итак, 

Если есть возможность вычислить AxB, то далеко не всегда можно вычислить BxA.

Например, А_2х3 * В_3х4=С_2х4

B_3x4*A_2x3 – умножить нельзя

Свойства перемножения матриц:

• A(BC)=(AB)C

• A(B+C)=AB+AC

• λ(AB)=A(λB)

• (AB)^т=B^тA^т

5. Транспонирование матрицы

Транспонированной по отношению к матрице А называется матрица, столбцы которой являются строками матрицы А с теми же номерами.

А=A_m,n, то А^т=A^т_n,m

Свойства:

(А+В)^т =А^т+В^т

(АВ)^т=В^т*А^т

2. Квадратные матрицы. Транспонирование матриц. Определитель квадратной матрицы. Свойства определителя.

Рассмотрим некоторые частные виды квадратных матриц.

1. Квадратная матрица называется диагональной, если все элементы, не стоящие на главной диагонали, равны нулю.

2. Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной. Обозначается:

3. Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю:

верхняя нижняя

треугольная матрица треугольная матрица

Для квадратной матрицы вводится понятие: определитель матрицы. Это определитель, составленный из элементов матрицы. Обозначается:

Ясно, что определитель единичной матрицы равен 1: Е = 1

ЗАМЕЧАНИЕ. Неквадратная матрица определителя не имеет.

Если определитель квадратичной матрицы отличен от нуля, то матрица называется невырожденной, если определитель равен нулю, то матрица называется вырожденной.

1.Если A=(a₁₁) – квадратная матрица первого порядка, то ее определителем (определителем первого порядка) называется число |А|=а₁₁

2.Если А= а₁₁ а₁₂

а₂₁ а₂₂

квадратная матрица второго порядка, то ее определителем (определителем второго порядка) называется число |А|=а₁₁а₂₂-а₁₂а₂₁

3.Если А= а₁₁ а₁₂ а₁₃

а₂₁ а₂₂ а₂₃

а₃₁ а₃₂ а₃₃

- квадратная матрица третьего порядка, то ее определителем (определителем третьего порядка) называется число

|А| = а₁₁а₂₂а₃₃+а₁₂а₂₃а₃₁+а₁₃а₂₁а₃₂-а₁₃а₂₂а₃₁-а₁₂а₂₁а₃₃-а₁₁а₂₃а₃₂

«ПРАВИЛО ЗВЕЗДЫ» - правило для вычисления определителя третьего порядка

Схема, обозначенная знаком «+», показывает, какие элементы входят сомножителями в первые три слагаемые, а схема, обозначенная знаком «–, показывает, какие элементы входят сомножителями в последние три слагаемые.

Свойства определителей:

1. Определитель квадратной матрицы равен определителю транспонированной матрицы

det A =det A^т

2. Если поменять местами два параллельных ряда (строку или столбец) матрицы, то ее определитель изменит только знак.

3. Определитель матрицы, имеющий две одинаковые строки или два одинаковых столбца, равен 0.

4. Общий множитель всех элементов какого-нибудь ряда матрицы можно вынести за знак определителя.

5. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.

6. Минором M_ij элемента a_ij определителя данной матрицы n-порядка, называется определитель матрицы, полученный из данной матрицы путем вычеркивания ее i-й строки и j-го столбца.

а₁₁ а₁₂ а₁₃ a₂₂ a₂₃

|А|= а₂₁ а₂₂ а₂₃ , то m₁₁= a₃₂ a₃₃

а₃₁ а₃₂ а₃₃

Алгебраическим дополнением Аij элемента a_ij определителя называется его минор, взятый со знаком «+», если сумма i+j - четное число, и со знаком «-», если эта сумма нечетная. Рассчитывается по формуле А_ij=(-1)^i+jM_ij

А₁₁=+m₁₁

А₃₂= -m₃₂

7. Определитель произведения двух квадратных матриц равен произведению определителей этих матриц.

8. Определитель матрицы, полученной из данной матрицы прибавлением к элементам какого-либо ряда соответствующих элементов параллельного ряда, умноженных на одно и то же число, равен определителю исходной матрицы.

а₁₁ а₁₂ а₁₃ а₁₁ а₁₂ а₁₃+k*a₁₂ a₁₁ a₁₂ a₁₃ a₁₁ a₁₂ a₁₂

|А|= а₂₁ а₂₂ а₂₃ = a₂₁ a₂₂ a₂₃+k*a₂₂ = a₂₁ a₂₂ a₂₃ + k*a₂₁ a₂₂ a₂₂ = |A|+k*0=|A|

а₃₁ а₃₂ а₃₃ a₃₁ a₃₂ a₃₃+k*a₃₂ a₃₁ a₃₂ a₃₃ a₃₁ a₃₂ a₃₂