- •Вопрос 5
- •Вопрос 13 подстановок группа- совокупность подстановок
- •26(37). Понятие логической функции. Способы задания логических функций.
- •1) Табличный способ
- •2) Числовой способ
- •3) Координатный способ
- •4) Аналитический способ
- •27(38). Булева алгебра. Основные свойства операций булевой алгебры. Понятие двойственности и самодвойственной логической функции.
- •28(39). Алгебра Жегалкина. Основные свойства операций алгебры Жегалкина.
- •29(40). Алгебра Жегалкина. Представление логических функций полиномом Жегалкина.
- •30(41). Разложение логической функции по переменным. Понятие совершенной дизъюнктивной нормальной формы логической функции. Понятие совершенной конъюнктивной нормальной формы логической функции.
- •31(42). Понятие полинома логической функции(полинома Жегалкина). Понятие линейной логической функции.
4) Аналитический способ
При этом способе функция задается в виде аналитического выражения, полученного путем применения каких-либо логических операций.
Например:
![]()
27(38). Булева алгебра. Основные свойства операций булевой алгебры. Понятие двойственности и самодвойственной логической функции.
Булева алгебра
Булевой алгеброй называется непустое множество A с двумя бинарными операциями (аналог конъюнкции), (аналог дизъюнкции), унарной операцией (аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a, b и c из множества A верны следующие аксиомы:
![]() ассоциативность
ассоциативность
![]()
![]() коммутативность
коммутативность
![]()
![]() законы
поглощения
законы
поглощения
![]()
![]() дистрибутивность
дистрибутивность
![]()
![]() дополнительность
дополнительность
![]()
Основные свойства операций булевой алгебры
Из аксиом видно, что наименьшим элементом является 0, наибольшим является 1, а дополнение ¬a любого элемента a однозначно определено. Для всех a и b из A верны также следующие равенства:
![]()
![]()
![]()
![]()
![]()
![]()
![]() дополнение
0 есть 1 и наоборот
дополнение
0 есть 1 и наоборот
![]()
![]() законы
де Моргана
законы
де Моргана
![]()
![]() инволютивность
отрицания, закон снятия двойного
отрицания.
инволютивность
отрицания, закон снятия двойного
отрицания.
Понятие двойственности и самодвойственной логической функции
Двойственная функция - это функция, полученная из исходной путём замены в ней всех переменных на противоположные. Закон двойственности гласит, если формулы А и В равносильны, то и двойственные им формулы А* и В* также равносильны. В теории исчисления высказываний этот закон назван принципом двойственности.
Функция, совпадающая со своей двойственной, называется самодвойственной.
28(39). Алгебра Жегалкина. Основные свойства операций алгебры Жегалкина.
Алгебра Жегалкина
Множество булевых функций, заданный в базисе Жегалкина S4={⊕,&,1} называется алгеброй Жегалкина.
Основные свойства операций алгебры Жегалкина
Основные свойства.
1. коммутативность H1⊕H2=H2⊕H1 H1&H2=H2&H1
|
2. ассоциативность H1⊕(H2⊕H3)=(H1⊕H2)⊕H3 H1&(H2&H3)=(H1&H2)&H3
|
3. дистрибутивность H1&(H2⊕H3)=(H1&H2)⊕(H1 &H3)
|
4. свойства констант H&1=H H&0=0 H⊕0=H
|
5. H⊕H=0 H&H=H
|
|
x
|
x(y z)=xy xz
|
x x=0
|
x 0=x
|
x
1=
|
xVy=xy x y
|
29(40). Алгебра Жегалкина. Представление логических функций полиномом Жегалкина.
Алгебра Жегалкина
Множество булевых функций, заданный в базисе Жегалкина S4={⊕,&,1} называется алгеброй Жегалкина.
Представление логических функций полиномом Жегалкина
Исходя из оценки числа различных функций алгебры логики и числа различных полиномов Жегалкина, следует
Теорема Жегалкина.
Для всякой логической функции существует соответствующий ей полином Жегалкина и притом только один.
Функция
алгебры логики, для которой полином
Жегалкина имеет вид
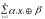 (здесь
знак суммирования означает суммирование
по модулю 2, а параметры
(здесь
знак суммирования означает суммирование
по модулю 2, а параметры
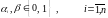 ,
называется линейной.
,
называется линейной.
Очевидно, что все функции от одной переменной линейны.
Линейными
являются, например, функции x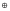 y
и
x
y
y
и
x
y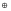 1=x~y.
1=x~y.
Для построения полинома Жегалкина можно воспользоваться следующими двумя схемами:
Схема 1.
Перейти в сигнатуру алгебры Жегалкина (это можно сделать всегда, так как система функций {x&y, x y, 1} , как это было показано ранее, полна), раскрыть скобки и провести возможные сокращения.
Схема 2.
Воспользоваться приёмом, который называется методом неопределённых коэффициентов.
Этот
метод применим лишь тогда, когда функция
от n переменных задана своей таблицей
истинности. Решается система линейных
уравнений с
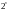 ограничениями, которые задаются через
значения функции на двоичных n мерных
наборах, и
неизвестными
- коэффициентами полинома Жегалкина.
ограничениями, которые задаются через
значения функции на двоичных n мерных
наборах, и
неизвестными
- коэффициентами полинома Жегалкина.
Пример составления полинома Жегалкина.
Возьмем СДНФ нашей функции, и упростим его, насколько возможно:
f(x,y,z) = (~x & y & z) (x & ~z)
Теперь преобразуем инверсии:
f(x,y,z)
= ((x
![]() 1) & y & z) (x & (z
1))
1) & y & z) (x & (z
1))
Теперь преобразуем операцию :
f(x,y,z) = ((x 1) & y & z) (x & (z 1)) ((x 1) & y & z & x & (z 1))
Раскроемскобки:
f(x,y,z) = (x & y & z) (1 & y & z) (x & z) (x & 1) (x & y & z & x & z)
(1 & y & z & x & z)
(x& y & z & x & 1) (1 & y & z & x & 1)
Применим законы поглощения внутри скобок:
f(x,y,z) = (x&y&z) (y&z) (x&z) x (y&x&z) (y&x&z) (y&z&x) (y&z&x)
Применим законы поглощения для одинаковых скобок, учитывая, что переменные, соединенные знаками & можно менять местами:
f(x,y,z) = (y & z) (x & z) x (x & y & z)

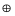 y=y
x
y=y
x