№1

1. МНОЖЕСТВО является неопределимым понятием математики как точка, прямая и плоскость. Вы столкнетесь с ним практически во всех науках – математике, физике, химии, истории и т.д. Под множеством понимают объединение в одно целое различных объектов. Порядок объектов во множестве не важен.Объекты, которые образуют множество, называют элементами множества. Для обозначения множеств обычно используют большие буквы, а для обозначения элементов используют малые буквыМножество можно описать как совокупность некоторых объектов (элементов множества), объединенных по какому-либо признаку. Множества могут быть конечными (состоящими из конечного числа элементов) и бесконечными. Количество элементов в конечном множестве называется его мощностью и обозначается |А|. Множество нулевой мощности, не содержащее элементов, называется пустым и обозначается . Множества, имеющие одинаковое количество элементов, называются равномощными. Класс всех рассматриваемых множеств называется универсальным множеством или универсумом (обозначается U). Множество М не содержащее ни одного элемента называют пустым и обозначают 0.

Множество А называют подмножеством множества В, если любой элемент А является элементом В. При этом говорят, что В содержит или покрывает А. Это обозначается А .В.

Пустое множество принято считать подмножеством любого множества.

Множества А и В равны (А=В| если они составлены из одних и тех же элементов (A B иВ А).

Мультимножество — в математике, обобщение понятия множества, допускающее включение одного и того же элемента по нескольку раз. СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВА.

1. диаграммы Эйлера-Венна. Это графическое изображение множеств в универсуме. Универсум изображается прямоугольником, внутри которого располагаются множества, иллюстрирующиеся овалами. Результирующее множество выделяется штриховкой.

2. перечисление элементов. А={а1 а2 а3 а4 а5 а6}. Списком можно задавать только конечные множества. В данном случае последовательность элементов множества в произвольном порядке записывается в фигурных скобках. Множество целых чисел от n до m обозначается Аn..m

ПРИМЕР. D-3.. 3 ={ -3, -2, -1, 0, 1, 2, 3}.

3. характеристический предикат. А={х| P(x)}. Это описание свойств элементов данного множества, где Р(х)- некоторое логическое выражение с логическим значением. Если результат Р(х) положителен (истинен), то элемент принадлежит множеству.

ПРИМЕР. D={nZ| -4<n<4}Такие задания могут приводить к противоречиям, таким как парадокс Рассела: класс всех множеств, не содержащих себя в качестве элемента: А={B| BB}. Имеем: АА, тогда АА и обратно: АА, тогда АА. (Задача о лгунах: я всегда вру.)

4. порождающая процедура. А={х| х=F}. Здесь F – процедура, при работе которой появляются элементы множества.

ПРИМЕР. А={1, 2, 4, 8, 16, …}={n| 1A (nA2nA)} Такое задание также называется рекурсивным. В курсе общей математики способ носит название математической индукции.

ОПЕРАЦИИ НАД МНОЖЕСТВАМИ.

1. объединение множеств. Это множество, состоящее из элементов, которые принадлежат хотя бы одному из этих множеств. АВ={ххА хВ}. Данная операция выполнима и для произвольного количества множеств (в т.ч. бесконечного):

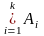
ПРИМЕР. А={2, 1, 5, 7} В={-6, -7, 0, 1, 5} АВ={-7, -6, 0, 1, 2, 5, 7}

2. пересечение множеств. Это множество, элементами которого являются только те элементы, которые присутствуют в каждом из множеств. АВ={ххА хВ}. Эта операция также возможна с произвольным количеством множеств: .

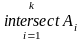ПРИМЕР. А={2, 1, 5, 7} В={-6, -7, 0, 1, 5} АВ={1, 5}

3. разность двух множеств. Это множество элементов, принадлежащих первому множеству и не являющихся элементами второго. А\В={ххА хВ}.

ПРИМЕР. А={2, 1, 5, 7} В={-6, -7, 0, 1, 5} А\В={2, 7}

4. симметрическая разность двух множеств. Это разность объединения этих множеств с их пересечением. А . В= (АВ)\( АВ) ={х (хА хВ)  (хА хВ)}.

ПРИМЕР. А={2, 1, 5, 7} В={-6, -7, 0, 1, 5} А\В={-7, -6, 0, 2, 7}

5. дополнение. Учитывая, что все множества образуют универсум, то дополнение –это множество элементов универсума, не являющиеся элементами данного множества. ={ххU хA}. В данном случае универсум должен быть либо задан, либо понятен из контекста задания.

№2

Вектор- это упорядоченный набор элементов или упорядоченное множество. Элементы – это координаты или компоненты вектора. Нумерация элементов производится слева направо. Векторы (а₁ , а₂), (а₁ , а₂ , а₃), (а₁ , а₂ , а₃ ,…) называют соответственно двойка, тройка, энка. Количество элементов в векторе называется длиной вектора. Равные векторы:  два вектора (а₁ , а₂ , а₃ ,…, а_n) и (b₁ , b₂ ,…, b_m) равны тогда и только тогда, когда n = m и а₁ = b₁ ,  а₂ = b₂ , …, а_n = b_m . Пример: {1, 2} = {2, 1, 1} = {2, 1}, но (1, 2)  (2, 1, 1)  (2, 1). Только (1, 2) = (1, 2).  Прямым (декартовым) произведением двух множеств А и В называется множество всех упорядоченных пар, в которых первая координата взята из первого множества, а вторая из второго. Прямое произведение множеств А₁ , А₂ , …, А_n  есть множество всех векторов (а₁ , а₂ , а₃ ,…, а_n) длины n таких , что а₁  А₁ , а₂  А₂ , …, а_п  А_п .Если  А₁ = А₂ = … = А_n , то А₁  А₂  …  А_n = Аⁿ и называется декартовой степенью.Если перемножаемые множества равны, то речь идет о степени множества: А*А=А² Теорема: мощность прямого произведения множеств равна произведению мощностей перемножаемых множеств.Доказательство: результатом прямого произведения множеств будет множество векторов, первые элементы которых можно выбрать |А1| способами, вторые координаты - |А2| и т.д., где |Аi| - мощность i-того множества. Таким образом мы имеем |А1|*|А2|*…*|Аn| векторов в полученном множестве.Следствие.|An|=|A|n. Теорема о мощности прямого произведения множеств. Принцип математической индукции Теорема. Пусть А₁ , А₂ , …, А_п – конечные множества и | А₁| = m₁ , |А₂| = m₂ , …,| А_п т„. Тогда \А_1* А2*...*А_n\= т_1* т_2*..т_n Доказательство данной теоремы проведем методом математической индукции. Данный метод применим для доказательства утверждений А(п), имеющих смысл для натуральных чисел п и заключается в следующем:Доказываем, что утверждение истинно для п= 1, т.е. А( 1) – истинно .Предполагаем, что А(k) - истинно, к=2,3,...Исходя из предположения А(к)- истинно доказываем истинность А(к+1). Из данного доказательства следует истинность утверждения А(п), для любого натурального числа п.В нашем случае для п= 1 истинность теоремы очевидна (А₁= т₁). Предположим, что теорема верна для к=2,3,..., т.е. \А_1*...*А_к\= т₁*...*т_к.

\

взаимооднозначное

соответствие

№3 Соответствием между множествами А и В называется подмножество G⊆A×B.Если (a, b) ∈ G, то говорят, что b соответствует а при соответствии G. Множество np₁G называется областью определения соответствия, множество np₂G — областью значений соответствия. Если np₁G = А, то соответствие называется всюду определенным (в противном случае соответствие называется частичным); если np₂G = В, то соответствие называется сюръективным. Элементы первых n-1множеств задают область определения соответствия (прообразы), последнего множества – область значений соответствия (образы). Говорят, что каждому вектору прообразов соответствует образ. Если область определения состоит из всех элементов образующих его множеств, то соответствие всюду определенное (инъективное), иначе частичное. Если область значений состоит из всего последнего множества соответствия, то соответствие сюръективное. Соответствие называется функциональным, оно всюду определено, сюръективно и любой прообраз имеет единственный образ. Если в функциональном соответствии каждому образу соответствует единственный прообраз, то это взаимнооднозначное соответствие. взаимнооднозначное соответствие. — это отображение, которое является одновременно и сюръективным, и инъективным. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом, определено обратное отображение, которое обладает тем же свойством №4 Отображение  называется полностью определенное функциональное соответствие между множествами А и В.

сюръективным отображением называется полностью определенное функциональное сюръективное соответствие между множествами А и В.Отображение называется инъективным, если прообразом любого элемента из области значения является единственный элемент из области определенияЕсли отображение инъективно и сюръективно, то оно называется биективным.Другими словами биективным отображением называется взаимно однозначное соответствие.Отображение называется инъекцией, если для любых элементов x1, x2 О X, для которых f(x1) = f(x2) следует, что x1 = x2. (рис. 7)Сюръекцией (или отображением "на" ) называется отображение, при котором f(X) = Y (рис. 8).Биекция – это одновременно и сюръекция и инъекция (рис.9).

Вопрос 5

Множества А и В называются равномощными, если между их элементами можно установить взаимнооднозначное соответствие. A ~ B  Счетное множество — это множество, эквивалентное множеству натуральных чисел. чётное множество – множество, элементы которого можно пронумеровать. Например, множества натуральных, чётных, нечётных чисел. Счётное множество может быть конечным (множество книг в библиотеке)    Несчетные - бесконечные множества, не равномощные множеству натуральных чисел. Мощность множества – это характеристика, которая объединяет данное множество с другими множествами, применение процедуры сравнения к которым дает основание предполагать, что каждый элемент одного множества имеет парный элемент из другого множества и наоборот.  Классифиция множества 1 Счетные  делятся :  А конечные и Б счетно-бесконечные  2 несчетные. Счетные  делятся : конечные и счетно-бесконечные. конечных множеств: конечные множества не равномощны никакому своему собственному подмножеству.

Счетно- бесконечных множеств: бесконечное собственное подмножество бесконечного множества может быть равномощно самому множеству Вопрос 6  Отношение — математическая структура, которая формально определяет свойства различных объектов и их взаимосвязи    Обычно отношения обозначают латинской буквой R Свойства отношений.

Отношения служат одним из способов заданиявзаимосвязи Между элементами множества. Наиболее изученными и чаще всего используемыми являются так называемые унарные и бинарные отношения. Для обозначения отношений мы будем использовать малые буквы греческого алфавита ρ, σ,τ и т.д. Унарное (одноместное) отношение соответствует наличию какого-то определенного признака (свойства) у элементов множества X(например, признак «быть отрицательным» на множестве Z целых чисел). Все элементы, обладающие выделенным признаком, образуют некоторое подмножество ρ⊂X. Это подмножество ρ и называют унарным отношением на множестве X Бинарные (двуместные) отношения используют как характеристику некоторой взаимосвязи между элементами множестваX. Элементами бинарного отношения являются упорядоченные пары прямого произведения X×X, и, следовательно, самобинарное отношение может быть задано как некоторое подмножество прямого произведенияρ⊂X×X. СВОЙСТВА ОТНОШЕНИЙ.

1. рефлексивность. Для любого элемента из А выполняется отношение аRа.

2. (aA) aRa. Главная диагональ такого отношения содержит только единицы. антирефлексивность. Для любого а из А отношение не выполняется. (aA) not(aRa). Главная диагональ его матрицы содержит только нули.

3. симметричность. Для любой пары отношение либо выполняется в обе стороны, либо вообще не выполняется.

(a,bA) (aRbbRa). Матрица симметрична относительно главной диагонали.

4. антисимметричность. Для любой пары отношение выполняется в обе стороны только в том случае, когда элементы пары равны.

(a,bA) (aRb=bRaa=b)

5. транзитивность. Для любых двух пар (a,b) и (b,c) выполнимость отношения для них говорит о выполнимости отношения для пары (а,с).

(a,b,cA) (aRb&bRcaRc)

6. полнота (линейность). Любые два элемента из множества А вступают в отношение хотя бы в одну сторону.

(a,bA) (a≠baRbbRa).

Вопрос7: Отношение называется отношением эквивалентности (или просто эквивалентностью), если оно рефлексивно, симметрично и транзитивно.Отношение эквивалентности ( ) на множестве   — это бинарное отношение, для которого выполнены следующие условия

вопрос8  На множестве А определена алгебраическая операция, если каждым двум элементам этого множества, взятым в определенном порядке, однозначным образом поставлен в соответствие некоторый третий элемент из этого же множества.Примерами алгебраических операций могут служить такие операции как сложение и вычитание целых чисел, сложение и вычитание векторов, матриц, умножение квадратных матриц, векторное умножение векторов и др.Отметим, что скалярное произведение векторов не может считаться алгебраической операцией, т.к. результатом скалярного произведения будет число, и числа не относятся к множеству векторов, к которому относятся сомножители. Ассоциативными называют операции, которые можно выполнять в произвольном порядке. По схеме: (x + y) + z = x + (y + z), где + - некоторая операция. Дистрибутивной называют пару операций, для которых работает схема раскрытия скобок, характерная для сложения и умножения в арифметике: x * (y + z) = (x * y) + (x * z) и  (x + y) * z = (x * z) + (y * z),  где * и + - некоторые логические операции. Пусть дано некоторое множество M, на котором задана совокупность операций 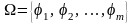. 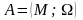Структура вида называется алгеброй; множество M называется несущим множеством, совокупность операций 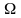- сигнатурой, вектор “ ” операций называется типом. Алгебраической системой <A;W_F;W_R> называется объект, состоящий из трёх множеств: непустого множества A, множества алгебраических операций W_F, определёных на A, и множества отношений W_R, определёных на A. Множество A называется носителем алгебраической системы. Если алгебраическая система не содержит операций, она называется моделью, если не содержит отношений, то – алгеброй. вопрос9. 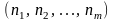Непустое множество M с бинарной операцией   называется группоидом. Иногда нам удобнее использовать обозначение Группоид   с бинарной операцией   называется полугруппой, если операция   ассоциативна; моноидом, если операция ассоциативна (т. е. это полугруппа) и в   существует нейтральный элемент e .Полугруппой называется алгебра вида 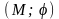с одной ассоциативной бинарной операцией 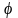.Как правило, в качестве такой операции используется умножение. Поэтому результат её применения к двум различным элементам записывают в виде или 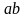, а результат неоднократного применения к одному элементу записывают в виде 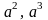и так далее. Такая запись называется мультипликативной. Полугруппу часто обозначают записью .Не следует понимать сказанное выше в том смысле, что полугруппа всегда включает в себя именно арифметическую операцию умножения. Термин “умножение” здесь является достаточно условным. Символ “ ” применяется именно для того, чтобы указать на это. Под символом“ ” может пониматься и произведение матриц или векторов, и композиция каких-либо преобразований, и даже сложение. В общем случае, (как, например, произведение матриц), то есть данная операция некоммутативна. Если же умножение коммутативно, то полугруппа называется коммутативной или абелевой полугруппой. вопрос10. Группой называется полугруппа с единицей, в которой для каждого элемента 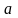существует элемент 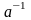, называемый обратным к элементу и удовлетворяющий условию 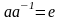. Различные множества могут образовывать группу относительно какой-либо операции и не являться группой относительно другой операции.Число элементов в множестве-носителе называется порядком группы. Группа, в которой операция коммутативна, называется коммутативной или абелевой. Группа, в которой все элементы являются степенями одного элемента, называется циклической. Для абелевых групп часто применяется аддитивная форма записи: операция обозначается, как сложение, а единица обозначается, как 0. вопрос11.Множество R с двумя определенными в нем алгебраическими операциями, сложением и умножением, называется кольцом, если относительно операции сложения оно является абелевой группой, а операция умножения дистрибутивна, т.е. для любых элементов a, b и с  R справедливы равенства: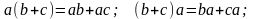 Если операция умножения, определенная в кольце коммутативна, то такое кольцо называется коммутативным кольцом.Из определения следует, что любое кольцо имеет две бинарные и одну унарную (см. пункт 2) операцию, поэтому его тип - 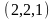.Непустое множество R называется кольцом, если в нем определены две алгебраические операции: сложение, ставящее в соответствие каждым двум элементам a, b элемент a + b, называемый их суммой, и умножение, ставящее в соответствие каждым двум элементамa, b элемент ab, называемый их произведением, причем эти операции обладают следующими свойствами:      I. (Коммутативность сложения) a + b = b + a;      II. (Ассоциативность сложения) a + (b + c) = (a + b) + c;  III. (Обратимость сложения) Для любых a и b из R уравнение a + x = b имеет (по крайней мере одно) решение, т. е. существует элемент  такой, что a + c = b;      IV. (Коммутативность умножения) ab = ba;  Термин "кольцо" применяется также ко множествам с некоммутативным или даже неассоциативным умножением. Формулировки других свойств также меняются.      V. (Ассоциативность умножения) a(bc) = (ab)c;   VI. (Дистрибутивность умножения относительно сложения) (a + b)c = ac + bc Примеры колец. При обычных операциях сложения и умножения кольцом является:      1. Множество целых чисел.2. Множество рациональных чисел. 3. Множество действительных чисел. 4. Множество рациональных чисел.   5. Множество, состоящее лишь из одного числа 0. 6. Множество четных чисел и вообще множество целых чисел, кратных некоторому числу n. 7. Множество комплексных чисел a + bi с целыми a и b (так называемое кольцо целых комплексных чисел). 8. Множество действительных чисел  , где a и b - целые числа. вопрос12.  Полем называется кольцо P, обладающее следующими свойствами:    VII. (Обратимость умножения) Для любых a и b из P, где a ≠ 0, уравнение ax = b имеет (покрайней мере одно) решение, т. е. существует элемент   такой, что aq = b. VIII. P содержит по крайней мере один элемент, отличный от нуля.Примеры:2. Множество рациональных чисел. 3.Множество действительных чисел. 4.Множество рациональных чисел