9. Эквивалентные формулы. Способы установления эквивалентности формул.

Формулы, представляющие одну и ту же функцию, называют эквивалентными или равносильными.

Стандартный метод установления эквивалентности: 1) по каждой формуле восстанавливается таблица истинности функции, а затем 2) полученные таблицы сопоставляются по каждому набору значений переменных.

13. Двойственность.

Функция f1(x1,…, xn) называется двойственной к функции f2(x1,…, xn), если .

Отношение двойственности между функциями симметрично. Из определения двойственности ясно, что для любой функции двойственная функция определяется однозначно. В частности, может оказаться, что функция двойственна самой себе. В этом случае она называется самодвойственной.

Примеры:

дизъюнкция двойственна конъюнкции;

константа 1 двойственна 0;

отрицание самодвойственно;

функция 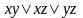самодвойственна.

Принцип двойственности: если в формуле F, представляющей функцию f, все знаки функций заменить соответственно на знаки двойственных функций, то полученная формула F* будет представлять функцию f*, двойственную к f.

14. Алгебра Вебба, алгебра Шеффера, импликативная алгебра, коимпликативная алгебра, алгебра Жегалкина.

• алгебра Вебба A = áMño ,;

• алгебра Шеффера A = áM, ñ½;

• импликативная алгебра A = áM,® , 0ñ;

• коимпликативная алгебра A = áM,® , 1ñ;

• алгебра Жегалкина A = áM, &, ,Å 1ñ.

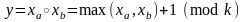
– - Трехзначная функция — функция Вебба.

Конечнозначная алгебра Вебба

16. Конечнозначные логики. Алгебра Вебба, алгебра Поста, алгебра Россера–Тьюкетта.

Функция, отображающая n-мерный k-значный кортеж в множество {0, 1, ..., k – 1}, называется функцией k-значной логики. Будем задавать функцию k-значной логики с помощью таблицы истинности (одномерной таблицы), число строк которой равно kn, или двумерной таблицы, число клеток которой равно k2.

Трехзначная функция — функция Вебба, заданная таблицами:

алгебра Поста

где дизъюнкция

цикл

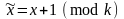
алгебра Россера—Тьюкетта

конъюнкция

характеристические функции

15.Полиномы Жегалкина. Процедура приведения к пнф.

Определение. Алгебра над множеством логических функций с двумя бинарными операциями называется алгеброй Жегалкина.

Замечание. Операция вполне аналогична операции конъюнкции (логического умножения). Однако операция имеет совершенно другой математический смысл, чем дизъюнкция (соответствующая функция ранее была названа неравнозначностью). Поэтому никак нельзя считать алгебру Жегалкина иной формой записи булевой алгебры.

В алгебре Жегалкина выполняются следующие соотношения (знак умножения опущен):

1.1. ,

1.2. ,

1.3 ,

1.4 .

Кроме того, выполняются соотношения, ранее сформулированные булевой алгебры, относящиеся к конъюнкции и константам. Отрицание и дизъюнкция выражаются так:

1.5 ,

1.6 .

Если в произвольной формуле алгебры Жегалкина раскрыть скобки и произвести все упрощения по вышеуказанным соотношениям, то получится формула, имеющая вид Суммы произведений, то есть полином (многочлен) по модулю 2. Такая формула называется полиномом Жегалкина для данной функции: P = a₀ + a₁x₁ +a₂x₂ + ...a_nx_n +a_{n +1}x₁x₂ +...+a_{n +C}²_nx_n-1x_n + ...+a_2n-1x₁x₂..xn означает сложение по модулю 2, коэффициенты a₀,a₁,..,a₂ⁿ_-1 являются константами (равными нулю или единице).

От булевой формулы всегда можно перейти к формуле алгебры Жегалкина, используя равенства 1.5 и 1.6, а также прямое следствие из равенства 1.6: если , то . Оно, в частности, позволяет заменять знак дизъюнкции знаком в случаях, когда исходная формула представляет собой СДНФ.

Пример:

Теорема. Любая функция п переменных может быть представлена полиномом Жегалкина и это представление единственно.

Доказательство. Любая функция f(x₁, x₂, …, x_n) имеет свою таблицу истинности. Запишем сначала данную функцию в виде полинома Жегалкина с неопределенными коэффициентами. Затем по очереди подставляем всевозможные наборы переменных и находим коэффициенты. Легко видеть, что за каждую подстановку находим только один коэффициент. Так как число наборов равно числу коэффициентов (и равно 2^п), отсюда следует утверждение теоремы.

Доказательство этой теоремы показывает, как по таблице истинности построить полином Жегалкина.

Имеется 2-й способ нахождения полинома Жегалкина для функций, заданных в виде ДНФ. Этот способ основан на 1.5. Если функция задана в виде ДНФ, то сначала убираем дизъюнкцию, используя при этом правило де Моргана, а все отрицания заменяем прибавлением единицы. После этого раскрываем скобки по обычным правилам, при этом учитываем, что четное число одинаковых слагаемых равно нулю (из-за 1.3), а нечетное число одинаковых слагаемых равно одному такому слагаемому.