23.Асимметрия и эксцесс.

Асимметрией (характеризует скошенность плотности распределения) называется число, обозначаемое А, равное: А= μ₃ / Ϭ₃

Эксцессом (характеризует островершинность распределения) называется число, обозначаемое Е:

Е= μ₄ / Ϭ₄-3

24.Функции случайных величин.

Пусть имеется НСВ Х с функцией плотности вероятности f(x). Другая СВY связана со СВ Х функциональной зависимостью: Y=φ(Х). Случайная точка (Х,Y) может находиться только на кривой у=φ(х).

Дифференциальная функция СВY определяется при условии, что φ(х) – монотонна на интервале (a,b), тогда для функции φ(х) существует обратная функция:

φ^-1=ψ, х= ψ(у).

Математическое ожидание и дисперсия СВ Х(Y=φ(Х)), имеющей дифференциальную функцию f(х): M(Y)=

D(Y)=

25.Биномиальный закон распеределения.

Пусть х – ДСВ равна числу появлений события в n-независимых испытаниях, в каждом из которых вероятность появления события равна p.

Биномиальным называют закон распределения ДСВ Х, если вероятность возможного значения х=k вычисляется по формуле Бернулли:

Р_n(k)=С^k_n * р^k * q^n-k.

MX=np

DX=npq

26.Закон пуассона.

Если n достаточно велико, а p очень мало, то используют приближенную формулу для вычисления вероятности:

Р_n(m) = λ^m* е^-λ / m!

Где λ=np. В таком случае говорят, что задан закон Пуассона с параметром λ.

MX=λ

DX=λ

27.Геометрическое и гипергеометрическое распределение.

ДСВ имеет геометрическое распределение, если она принимает значения k=1,2,3,… с вероятностями р_k=p*q^k-1

MX=1/p

DX=q/p²

ДСВ имеет гипергеометрическое распределение, если она принимает значения mc вероятностями:

Р(m)=P(X=m)=C^m_M*C^n-m_N-M/Cⁿ_N

Вероятность Р(m) является вероятностью выбора m-объектов, обладающих заданным свойством из n-объектов, случайно извлеченных из совокупности N-объектов, среди которых M-объекты обладают заданными свойствами.

MX=n*M/N

DX=n*(M/N-1)*(1-M/N)*(1-n/N)

28.РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ.

Говорят, что НСВ Х распределена равномерно на отрезке (a,b), если ее плотность р(х) постоянна на этом отрезке и равна нулю вне его.

Р(х)=

F(x)=

MX=(a+b)/2

DX=(b-a)²/12

29.ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ.

Говорят, что НСВ Х имеет показательное распределение с параметром λ, если ее плотность вероятности имеет следующий вид:

F(х)=

F(х)=

MX=1/x

DX=1/x²

30.НОРМАЛЬНЫЙЗАКОН РАСПРЕДЕЛЕНИЯ.

НСВ Х имеет нормальное распределение (Гаусса) с параметрами а и Ϭ, если ее плотность вероятности имеет вид:

Р(Х)=1/ *Ϭ)*e^-(x-a)²/2Ϭ²

Множество СВ нормально распределенных с параметрами а и Ϭ обозначается N (а,Ϭ).

F(x)= 1/ *Ϭ)

MX=a

DX=Ϭ²

31.ФУНКЦИЯ ЛАПЛАСА.

Вероятность того, что из n-независимых испытаний в каждом из которых вероятность появления события равна р(0<р<1), событие наступит не менее k₁ раз и не более k₂ раз, равна: Р_n (k₁, k₂)=Ф(х₂)-Ф(х₁), где Ф(х) – функция Лапласа,

х₁=k₁-np / ; х₂=k₂-np /

Свойства функции:

1. Ф(-х)=-Ф(х) – функция нечетная, поэтому достаточно применять ее для неотрицательных значений х:

Ф(х)=1/

2. Функция Ф(х) возрастает на всей числовой оси

3. При х≥4, Ф(х)=0,5

4. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях не более чем на некоторое число ε>0:Р_n(|m/n-p|<ε)=2Ф(ε* )
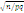