15.Случайные величины и их классификация.

Случайной величиной называют такую величину, которая в результате опыта может принимать те или иные значения, причем до опыта мы не можем сказать, какое именно значение она примет. (Более того, СВ – это действительная функция, определенная на пространстве элементарных событий Ω). СВ обозначаются последними буквами латинского алфавита – X, Y, Z. СВ могут быть трех типов: -дискретные,

-непрерывные,

-смешанные.

16.Дискретные и непрерывные величины.

Дискретная случайная величина (ДСВ) может принимать конечное или бесконечное счетное число значений. Непрерывная случайная величина (НСВ) в отличие от ДСВ принимает бесконечное несчетное число значений.

17.Законы распределения св.

Закон распределения СВ – это перечень ее возможных значений и соответствующих им вероятностей.

Законы распределения ДСВ:

1)закон распределения Бернулли,

2)биномиальный ЗР,

3)ЗР Пуассона,

4)геометрический ЗР,

5)геометрический ЗР, сдвинутый на единицу,

6)гипергеометрический ЗР.

Для НСВ:

1. равномерный ЗР,

2. показательное распределение,

3. нормальный ЗР.

18.Функция распределения и ее свойства.

Функция F (х)=Р (Х<х) называется интегральной функцией распределения.

Свойства интегральной функции распределения: 1) F (х) не убывает (если х₂>х₁, то F (x₂)≥F (х₁)).

2) F (-∞)=0.

3) F (+∞)=1.

4) Вероятность попадания СВХ в интервал а<Х<b:

Р (а≤Х<b)=F(b)-F(a).

Дифференциальной функциейСВХ называется производная ее функции распределения:

f(х)=F ‘ (х).

Свойства дифференциальной функции:

1. f (х)≥0.

2. 

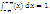
3. F (х) =

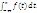
19.Плотность распределения нсв и ее свойства.

Плотностью распределения вероятностей НСВ Х называется такая функция р (х)≥0, что F (х)=

Свойства плотности: 1) р (х)≥0,

2)

3) p (х) = f ’(х)

4) р (а≤х≤в) =

20.Математическое ожидание и дисперсия св.

Математическое ожидание М (Х) ДСВ Х – это сумма парных произведений СВ на соответствующую вероятность: М (х)=х₁р₁+х₂р₂+…+х_nр_n.

Свойства математического ожидания:

1. М (С) = С

2. М (СХ) = С*М (Х)

3. Математическое ожидание суммы равно сумме математических ожиданий слагаемых.

Дисперсией ДСВ Х называется математическое ожидание квадрата отклонения СВ от ее математического ожидания:

D(X)=M((x-M(X))²)

Свойства дисперсии:

1. D(C)=0

2. D(CX)=C²D(X)

3. D(X)=M(X)²-(M(X))²

4. D(C+Х)=D(X)

Математическое ожидание для НСВ:

МХ=

Дисперсия для НСВ:

DX=

Все свойства дисперсии и математического ожидания, установленные для ДСВ, сохраняются для НСВ.

21.Мода и медиана.

Мода М_о(Х) распределения – это значение СВ, имеющее наиболее вероятное значение. Для НСВ (Мо(Х)) это точка локального максимума плотности.

Если мода единственна, то распределение СВ называется унимодальным, в противном случае полимодальным.

Медиана М_е(Х) – это значение случайной величины, которое делит таблицу распределения на две части таким образом, что вероятность попадания в одну из них равна 0,5. Медиана обычно не определяется для ДСВ.

22.Моменты св.

Начальным моментом порядка sназывается математическое ожидание степени sСВХ:

α_s = М(Х^s) Для ДСВ:

α_s = х^s₁р₁+ х^s₁р_2+…+ х^s₁р_n

Для НСВ:

α_s =

Отклонение СВ от ее математического ожидания называется центрированной СВ Х: Х=Х-m_x

Центральным моментом порядка sСВ Х называется математическое ожидание степени s, соответствующей центрированной СВ:

μ_s= μ(X^s)=M((x-m_x)^s)

Для ДСВ:

μ_s=

Для НСВ:

μ_s=

Основным моментом порядка sназывается нормированный центральный момент порядка S:

r_s = μ_s/ Ϭ_s