66.Обобщенные ординаты и обобщенные силы

Обобщённые силы

Перевод

Обобщённые силы

        величины, играющие роль обычных сил, когда при изучении равновесия или движения механической системы её положение определяется обобщёнными координатами (См. Обобщённые координаты). Число О. с. равно числу s степеней свободы системы; при этом каждой обобщённой координате q_i соответствует своя О. с. Q_i. Значение О. с. Q_i, соответствующей координате q_i, можно найти, вычислив элементарную работу δA₁ всех сил на возможном перемещении системы, при котором изменяется только координата q_i, получая приращение δq₁. Тогда δA₁ = Q₁δq₁, т.е. коэффициент при δq_i в выражении δA₁ и будет О. с. Q₁. Аналогично вычисляются Q₂, Q₃,..., Q_s. Например, если для лебёдки (рис.) вместе с поднимаемым ею на тросе грузом весом Р (система с одной степенью свободы) принять за обобщённую координату q_i угол φ поворота вала лебёдки и если к валу приложены вращающий момент М_вр и момент сил трения М_тр, то в данном случае δA₁ = (М_вр—М_тр—Pr)δφ, где r — радиус вала (весом троса пренебрегаем). Следовательно, для этой системы О. с., соответствующей координате j, будет Q₁ =М_вр—М_тр—Pr.

         Размерность О. с. зависит от размерности обобщённой координаты. Если размерность q_i — длина, то Q_i имеет размерность обычной силы; если q_i — угол, то Q_i имеет размерность момента силы (См. Момент силы) и т.д. При изучении движения механической системы О. с. входят вместо обычных сил в Лагранжа уравнения механики, а при равновесии все О. с. равны нулю. Например, для рассмотренной выше лебёдки при равномерном подъёме груза должно быть Q_i = 0, т. е. М_вр = М_тр + Pr.

         С. М. Тарг.

        

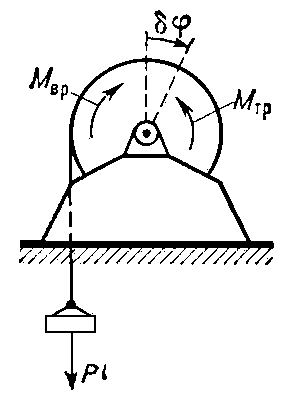
        Рис. к ст. Обобщённые силы.

Обобщённые координаты

Перевод

Обобщённые координаты

        независимые между собой параметры q_i (r = 1, 2,..., s) любой размерности, число которых равно числу s степеней свободы механич. системы и которые однозначно определяют положение системы. Закон движения системы в О. к. даётся s уравнениями вида q_i = q_i (t), где t — время. О. к. пользуются при решении многих задач, особенно когда система подчинена связям, налагающим ограничения на её движение. При этом значительно уменьшается число уравнений, описывающих движение системы, по сравнению, например, с уравнениями в декартовых координатах (см. Лагранжа уравнения в механике). В системах с бесконечно большим числом степеней свободы (сплошные среды, физические поля) О. к. являются особые функции пространственных координат и времени, называются потенциалами, волновыми функциями (См. Волновая функция) и т.п.

67.Уравнение Лагранжа второго рода

Уравнения Лагранжа 2-го рода:  , (i=1,2…s) – дифференциальные уравнения второго порядка, s – число степеней свободы системы (число независимых координат); q_i – обобщенная координата (перемещение, угол, площадь и др.); – обобщенная скорость (линейная скорость, угловая, секторная и др.),

Т = Т(q₁,q₂,…,q_S, , … ,t) – кинетическая энергия системы, Q_i – обобщенная сила (сила, момент и др.), ее размерность зависит от размерности обобщенной координаты и размерности работы.

Для вычисления обобщенной силы, например Q₁, задаем возможное перемещение, при котором все вариации обобщенных координат, кроме q₁, равны нулю:

q₁0, q₂= q₃=…= q_S= 0. Вычисляем на этом перемещении возможную работу А₁ всех активных сил, приложенных к системе. Имея  А₁= Q₁q₁, находим .

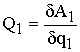Если силы, действующие на систему, потенциальные (консервативные) (например, силы тяжести, силы упругости), то ,   П = П(q₁,q₂,…,q_S,t) – потенциальная энергия.

Вводится функция Лагранжа:  L = T – П, тогда 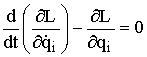   – уравнения Лагранжа второго рода для консервативной системы.

При стационарных связях (связях, не зависящих от времени) t не входит в выражение для кинетической энергии, тогд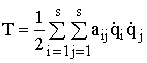а  – квадратичная форма обобщенных скоростей,  a_ij= a_ji – коэффициенты инерции. Квадратичная форма всегда положительна.